初中数学北师大版九上2.6.1应用一元二次方程教学设计
文档属性
| 名称 | 初中数学北师大版九上2.6.1应用一元二次方程教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 97.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:02:16 | ||
图片预览


文档简介
2.6.1应用一元二次方程
一、教学目标
1.掌握列一元二次方程解决几何问题、数学问题,并能根据具体问题的实际意义,检验结果的合理性.
2.理解将实际问题抽象为方程模型的过程,并能运用所学的知识解决问题.
二、教学重难点
重点:列一元二次方程解决实际问题.
难点:理解实际问题中的变化的量,寻找正确的等量关系.
三、教学方法
本课时教学内容主要是通过对实际问题的分析,进一步理解方程是刻画客观世界的有效模型,培养学生在生活中发现问题,解决问题的能力.
本节课首先提供了具体的情境,然后在具体的情境中逐步地展开对列方程解决实际问题的探讨,最后通过例题和练习加以巩固.
四、教学设计
(一)复习回顾
问题1:列方程解应用题的一般步骤是:
1.审:审清题意
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解,是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
问题2:列方程解应用题的关键是什么?
找出相等关系.
(二)问题探究
例1:如图,某海军基地位于A处,在其正南方向200 n mile 处有一目标B,在B的正东方向200 n mile处有一重要目标C. 小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D与小岛F相距多少海里
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF=AB,
∵AB⊥BC, AB = BC =200 n mile,
∴DF⊥BC, DF =100 n mile.
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300-2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300-2x)2.
整理得: 3x2-1200x + 100000 = 0 ,
解方程得 (舍)
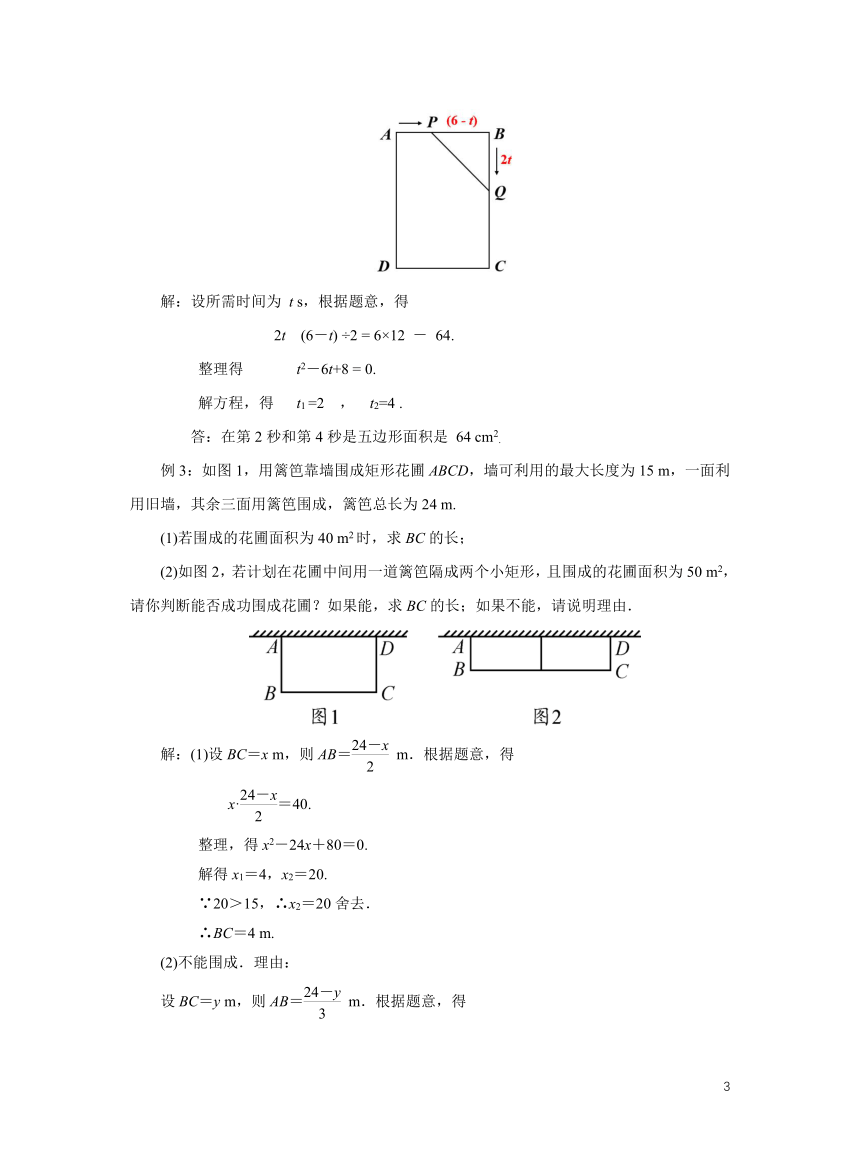
例2:如图,在矩形ABCD中,AB=6 cm, BC=12 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC向点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64 cm2?
解:设所需时间为 t s,根据题意,得
2t (6-t) ÷2 = 6×12 - 64.
整理得 t2-6t+8 = 0.
解方程,得 t1 =2 , t2=4 .
答:在第2秒和第4秒是五边形面积是 64 cm2.
例3:如图1,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15 m,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24 m.
(1)若围成的花圃面积为40 m2时,求BC的长;
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50 m2,请你判断能否成功围成花圃?如果能,求BC的长;如果不能,请说明理由.
解:(1)设BC=x m,则AB= m.根据题意,得
x·=40.
整理,得x2-24x+80=0.
解得x1=4,x2=20.
∵20>15,∴x2=20舍去.
∴BC=4 m.
(2)不能围成.理由:
设BC=y m,则AB= m.根据题意,得
y·=50.
整理,得y2-24y+150=0.
∵Δ=(-24)2-4×1×150=-24<0,∴该方程无实数根.
∴不能围成面积为50 m2的花圃.
(三)归纳总结
(三)课堂演练
1.将一块矩形铁皮的四个角各剪去一个边长为1 m的正方形后,剩下的部分刚好围成一个容积为15 m3的无盖长方体水箱,且此长方体水箱的底面长比宽多2 m,求该矩形铁皮的长和宽各是多少米.若设该矩形铁皮的宽是x m,则根据题意可得方程为( B )
A.(x+2)(x-2)×1=15 B.x(x-2)×1=15
C.x(x+2)×1=15 D.(x+4)(x-2)×1=15
2.一个直角三角形三边长是三个连续偶数,则这三条边的长分别为__6,8,10__,它的面积为__24___.
3.A、B、C、D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动,P、Q两点从开始出发__或_s时,点P和点Q的距离是10 cm.
4.如图,在Rt△ABC中,AC=6 cm,BC=8 cm.点M从点A出发,以每秒1 cm的速度沿AC方向运动;同时点N从点C出发,以每秒2 cm的速度沿CB方向运动,当点N到达点B时,点M同时停止运动.
(1)运动几秒时,△CMN的面积为8 cm2
(2)△CMN的面积能否等于12 cm2?若能,求出运动时间;若不能,请说明理由.
解:(1)设运动t s后△CMN的面积等于8 cm2. 根据题意,得
CM=6-t,CN=2t,则S△CMN=CM·CN=×(6-t)×2t=8.
解得t1=2,t2=4,故经过2 s或4 s后,△CMN的面积等于8 cm2.
(2)△CMN的面积不能等于12 cm2.理由:
S△CMN=MN·CN=×(6-t)×2t=-t2+6t=-(t-3)2+9,
则当t=3时,△CMN的面积最大为9 cm2,
∴△CMN的面积不能等于12 cm2.
(五)课堂小结
1.用一元二次方程解决实际问题要经历怎样的过程
[一审、二设、三列(列代数式、列方程)、四解、五验、六答]
2.用一元二次方程解决问题的关键是什么
(寻找题中的等量关系)
(设计意图:回顾列方程解应用题的过程,形成知识体系.)
(六)布置作业
教材第53页习题2.9第2,3题.
五、板书设计
2.6.1 应用一元二次方程 1.例题 2.练习 3.小结
六、教学反思
建构主义主张的教学方法,其核心是强调学习者是一个主动的、积极的知识构造者,教师的教学工作就是要从学生的实际出发,以深入了解学生真实的思维活动为基础,通过提供适当的问题情境或实例促使学生反思,引起学生必要的认知冲突,从而让学生最终通过其主动的思考建构起新的认知结构.
本节课的内容主要是对通过对实际问题的分析,进一步理解方程是刻画客观世界的有效模型,培养学生在生活中发现问题、解决问题的能力.整节课的设计关系生活的实用性,体现了“数学和生活的密切联系”.
1
一、教学目标
1.掌握列一元二次方程解决几何问题、数学问题,并能根据具体问题的实际意义,检验结果的合理性.
2.理解将实际问题抽象为方程模型的过程,并能运用所学的知识解决问题.
二、教学重难点
重点:列一元二次方程解决实际问题.
难点:理解实际问题中的变化的量,寻找正确的等量关系.
三、教学方法
本课时教学内容主要是通过对实际问题的分析,进一步理解方程是刻画客观世界的有效模型,培养学生在生活中发现问题,解决问题的能力.
本节课首先提供了具体的情境,然后在具体的情境中逐步地展开对列方程解决实际问题的探讨,最后通过例题和练习加以巩固.
四、教学设计
(一)复习回顾
问题1:列方程解应用题的一般步骤是:
1.审:审清题意
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:列代数式,列方程;
4.解:解所列的方程;
5.验:是否是所列方程的解,是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
问题2:列方程解应用题的关键是什么?
找出相等关系.
(二)问题探究
例1:如图,某海军基地位于A处,在其正南方向200 n mile 处有一目标B,在B的正东方向200 n mile处有一重要目标C. 小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰沿A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D与小岛F相距多少海里
解:连接DF.∵AD=CD , BF=CF,
∴DF是△ABC的中位线.
∴DF∥AB,且DF=AB,
∵AB⊥BC, AB = BC =200 n mile,
∴DF⊥BC, DF =100 n mile.
(2)已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
解: 设相遇是补给船航行了x n mile,那么
DE = x n mile , AE + BE = 2x n mile,
EF=AB +BF-(AB + BE) =(300-2x)n mile.
在Rt△DEF中,根据勾股定理可得方程
x2 = 1002 + (300-2x)2.
整理得: 3x2-1200x + 100000 = 0 ,
解方程得 (舍)
例2:如图,在矩形ABCD中,AB=6 cm, BC=12 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC向点C以2 cm/s的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64 cm2?
解:设所需时间为 t s,根据题意,得
2t (6-t) ÷2 = 6×12 - 64.
整理得 t2-6t+8 = 0.
解方程,得 t1 =2 , t2=4 .
答:在第2秒和第4秒是五边形面积是 64 cm2.
例3:如图1,用篱笆靠墙围成矩形花圃ABCD,墙可利用的最大长度为15 m,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24 m.
(1)若围成的花圃面积为40 m2时,求BC的长;
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50 m2,请你判断能否成功围成花圃?如果能,求BC的长;如果不能,请说明理由.
解:(1)设BC=x m,则AB= m.根据题意,得
x·=40.
整理,得x2-24x+80=0.
解得x1=4,x2=20.
∵20>15,∴x2=20舍去.
∴BC=4 m.
(2)不能围成.理由:
设BC=y m,则AB= m.根据题意,得
y·=50.
整理,得y2-24y+150=0.
∵Δ=(-24)2-4×1×150=-24<0,∴该方程无实数根.
∴不能围成面积为50 m2的花圃.
(三)归纳总结
(三)课堂演练
1.将一块矩形铁皮的四个角各剪去一个边长为1 m的正方形后,剩下的部分刚好围成一个容积为15 m3的无盖长方体水箱,且此长方体水箱的底面长比宽多2 m,求该矩形铁皮的长和宽各是多少米.若设该矩形铁皮的宽是x m,则根据题意可得方程为( B )
A.(x+2)(x-2)×1=15 B.x(x-2)×1=15
C.x(x+2)×1=15 D.(x+4)(x-2)×1=15
2.一个直角三角形三边长是三个连续偶数,则这三条边的长分别为__6,8,10__,它的面积为__24___.
3.A、B、C、D为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动,P、Q两点从开始出发__或_s时,点P和点Q的距离是10 cm.
4.如图,在Rt△ABC中,AC=6 cm,BC=8 cm.点M从点A出发,以每秒1 cm的速度沿AC方向运动;同时点N从点C出发,以每秒2 cm的速度沿CB方向运动,当点N到达点B时,点M同时停止运动.
(1)运动几秒时,△CMN的面积为8 cm2
(2)△CMN的面积能否等于12 cm2?若能,求出运动时间;若不能,请说明理由.
解:(1)设运动t s后△CMN的面积等于8 cm2. 根据题意,得
CM=6-t,CN=2t,则S△CMN=CM·CN=×(6-t)×2t=8.
解得t1=2,t2=4,故经过2 s或4 s后,△CMN的面积等于8 cm2.
(2)△CMN的面积不能等于12 cm2.理由:
S△CMN=MN·CN=×(6-t)×2t=-t2+6t=-(t-3)2+9,
则当t=3时,△CMN的面积最大为9 cm2,
∴△CMN的面积不能等于12 cm2.
(五)课堂小结
1.用一元二次方程解决实际问题要经历怎样的过程
[一审、二设、三列(列代数式、列方程)、四解、五验、六答]
2.用一元二次方程解决问题的关键是什么
(寻找题中的等量关系)
(设计意图:回顾列方程解应用题的过程,形成知识体系.)
(六)布置作业
教材第53页习题2.9第2,3题.
五、板书设计
2.6.1 应用一元二次方程 1.例题 2.练习 3.小结
六、教学反思
建构主义主张的教学方法,其核心是强调学习者是一个主动的、积极的知识构造者,教师的教学工作就是要从学生的实际出发,以深入了解学生真实的思维活动为基础,通过提供适当的问题情境或实例促使学生反思,引起学生必要的认知冲突,从而让学生最终通过其主动的思考建构起新的认知结构.
本节课的内容主要是对通过对实际问题的分析,进一步理解方程是刻画客观世界的有效模型,培养学生在生活中发现问题、解决问题的能力.整节课的设计关系生活的实用性,体现了“数学和生活的密切联系”.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
