初中数学北师大版九上4.3相似多边形教学设计
文档属性
| 名称 | 初中数学北师大版九上4.3相似多边形教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 125.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:09:53 | ||
图片预览

文档简介
4.3相似多边形
一、教学目标
1.了解相似多边形和相似比的概念.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据相似比进行相关的计算.
二、教学重难点
重点:相似多边形、相似比的概念.
难点:相似形的对应角相等,对应边成比例的性质,相似比的有序性.
三、教学方法
本节课主要内容是探究相似多边形和相似比的概念,通过引导学生观察、操作、归纳相似多边形、相似比的概念、特征.
根据本课时的特点,教学设计共设计了五个教学环节,首先通过计算创设情境引出相似多边形的概念,然后探究相似比的概念以及表示方法.在例题和练习中,通过对知识的运用,渗透学数学、用数学的理念.在课堂教学中,教师要注重学习方法的指导和探究知识能力的培养.
四、教学设计
(一)情境导入
想一想:下面几组图形有什么相同点和不同点
(二)问题探究
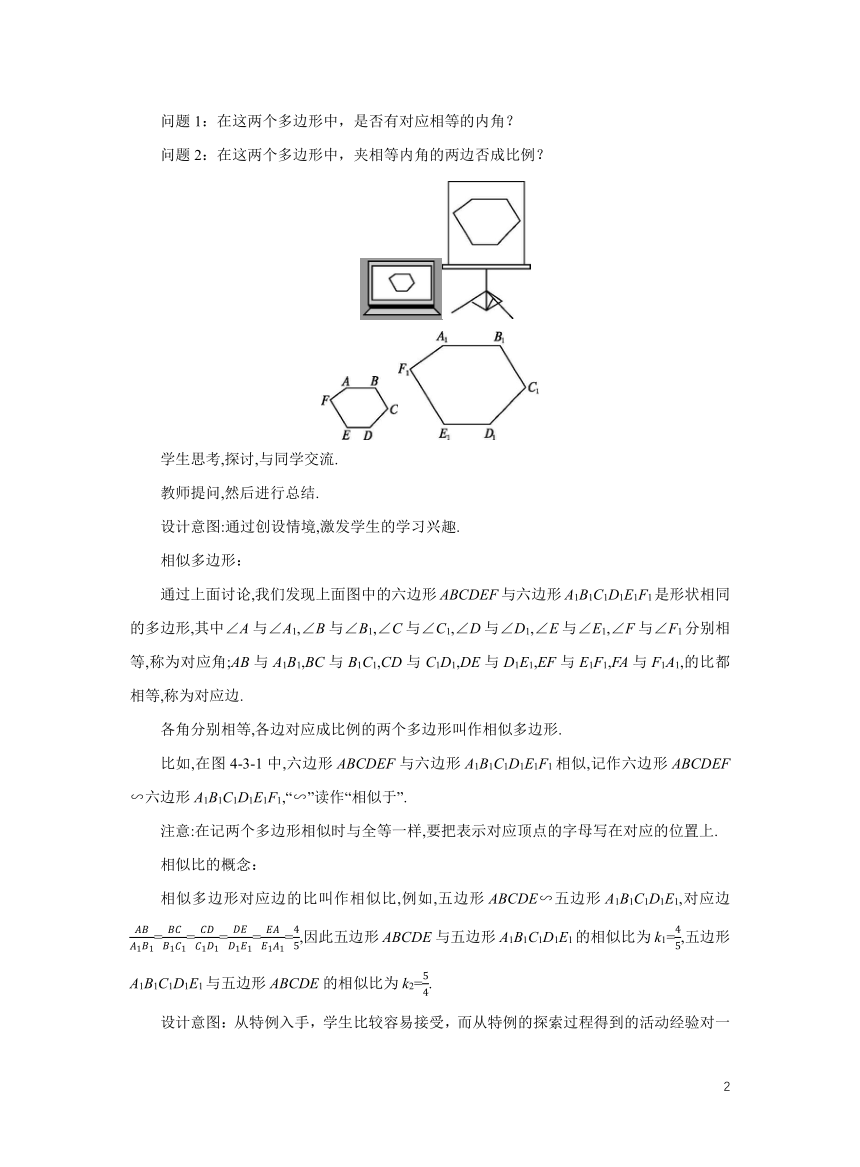
图中的两个多边形分别是计算机显示屏上的多边形ABCDEF和投射到银幕上的多边形A1B1C1D1E1F1.
问题1:在这两个多边形中,是否有对应相等的内角?
问题2:在这两个多边形中,夹相等内角的两边否成比例?
学生思考,探讨,与同学交流.
教师提问,然后进行总结.
设计意图:通过创设情境,激发学生的学习兴趣.
相似多边形:
通过上面讨论,我们发现上面图中的六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的多边形,其中∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1,的比都相等,称为对应边.
各角分别相等,各边对应成比例的两个多边形叫作相似多边形.
比如,在图4-3-1中,六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1,“∽”读作“相似于”.
注意:在记两个多边形相似时与全等一样,要把表示对应顶点的字母写在对应的位置上.
相似比的概念:
相似多边形对应边的比叫作相似比,例如,五边形ABCDE∽五边形A1B1C1D1E1,对应边=====,因此五边形ABCDE与五边形A1B1C1D1E1的相似比为k1=,五边形A1B1C1D1E1与五边形ABCDE的相似比为k2=.
设计意图:从特例入手,学生比较容易接受,而从特例的探索过程得到的活动经验对一般情况的探索起到铺垫的作用,从而降低难度.
特殊的相似多边形的探究.
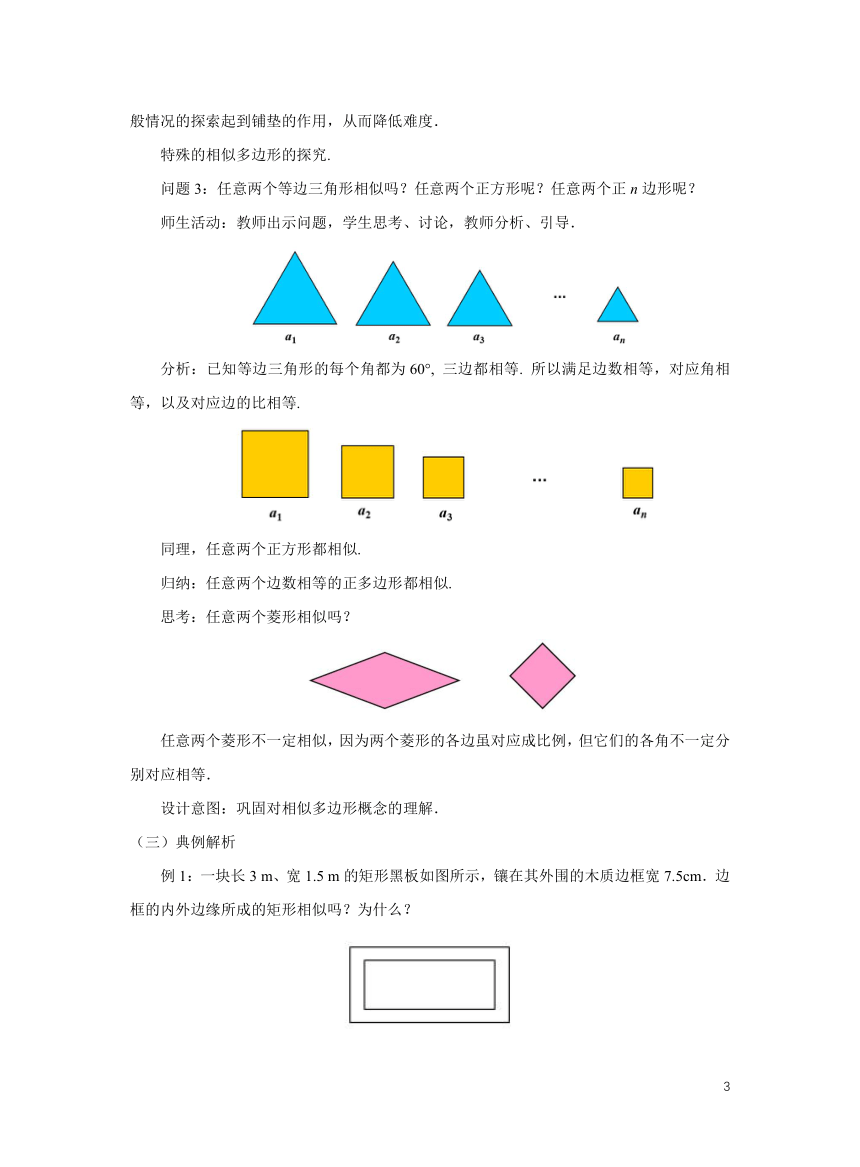
问题3:任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
师生活动:教师出示问题,学生思考、讨论,教师分析、引导.
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
思考:任意两个菱形相似吗?
任意两个菱形不一定相似,因为两个菱形的各边虽对应成比例,但它们的各角不一定分别对应相等.
设计意图:巩固对相似多边形概念的理解.
(三)典例解析
例1:一块长3 m、宽1.5 m的矩形黑板如图所示,镶在其外围的木质边框宽7.5cm.边框的内外边缘所成的矩形相似吗?为什么?
师生活动:教师出示问题,学生思考、讨论,教师引导学生应用相似多边形的定义判断.
答:不相似;因为,所以对应边不成比例.所以这两个矩形不相似.
设计意图:加深对相似多边形概念的理解.
例2:如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等,由此可得
α=∠C=83°,∠A=∠E=118°.
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
因为四边形ABCD和EFGH相似,
所以它们的对应边成比例,由此可得
,即.
解得x=28.
设计意图:通过求相似多边形的对应边、角,巩固相似多边形的概念及性质.
例3:如图,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴.
∴EF2=AD·BC=3×4=12,
∴EF=2.
∵四边形AEFD∽四边形EBCF,
∴AE:EB=AD:EF=3: 2=:2.
设计意图:通过例题,进一步巩固相似多边形和相似比的概念,让学生加强理解.
(四)课堂演练
1.下列命题中,正确的是( )
A.所有的等腰三角形都相似 B.所有的直角三角形都相似
C.所有的等边三角形都相似 D.所有的矩形都相似
2.若△ABC∽△ A′B′C′,且AB:A′B′=1:2
则△ABC与△ A′B′C′相似比是 ,△ A′B′C′与△ABC的相似比是 .
3. 如图所示的两个四边形是否相似?
4. 填空:
(1) 如图①是两个相似的四边形,则x= ,y = , α= ;
(2) 如图②是两个相似的矩形, x= .
设计意图:让学生自己小结,自己对本节课知识进行整合,培养学生养成一种对所学知识进行归纳总结的习惯.
(五)课堂小结
1.什么是相似多边形与相似比
2.怎么说明两个多边形是相似多边形
设计意图:让学生自己小结,自己对本节课知识进行整合,培养学生养成一种对所学知识进行归纳总结的习惯.
(六)布置作业
教材第88页习题4.4第1,2题.
五、板书设计
4.3 相似多边形
1.相似多边形及其相关概念
2.相似多边形的性质
3.典例解析
4.小结
六、教学反思
本节课的重点是相似多边形和相似比的概念和特征的学习,问题设计让学生参与到教学活动中,锻炼学生的观察、比较和归纳能力,并渗透类比的数学思想:让学生通过观察、猜想等方法,得出相似多边形的概念,帮助学生更加深入透彻地理解;最后通过一系列习题的演练,巩固所学知识,提高辨认图形的能力,为后续课程的学习打下基础.
1
一、教学目标
1.了解相似多边形和相似比的概念.
2.会根据条件判断两个多边形是否为相似多边形.
3.掌握相似多边形的性质,能根据相似比进行相关的计算.
二、教学重难点
重点:相似多边形、相似比的概念.
难点:相似形的对应角相等,对应边成比例的性质,相似比的有序性.
三、教学方法
本节课主要内容是探究相似多边形和相似比的概念,通过引导学生观察、操作、归纳相似多边形、相似比的概念、特征.
根据本课时的特点,教学设计共设计了五个教学环节,首先通过计算创设情境引出相似多边形的概念,然后探究相似比的概念以及表示方法.在例题和练习中,通过对知识的运用,渗透学数学、用数学的理念.在课堂教学中,教师要注重学习方法的指导和探究知识能力的培养.
四、教学设计
(一)情境导入
想一想:下面几组图形有什么相同点和不同点
(二)问题探究
图中的两个多边形分别是计算机显示屏上的多边形ABCDEF和投射到银幕上的多边形A1B1C1D1E1F1.
问题1:在这两个多边形中,是否有对应相等的内角?
问题2:在这两个多边形中,夹相等内角的两边否成比例?
学生思考,探讨,与同学交流.
教师提问,然后进行总结.
设计意图:通过创设情境,激发学生的学习兴趣.
相似多边形:
通过上面讨论,我们发现上面图中的六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的多边形,其中∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1,的比都相等,称为对应边.
各角分别相等,各边对应成比例的两个多边形叫作相似多边形.
比如,在图4-3-1中,六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1,“∽”读作“相似于”.
注意:在记两个多边形相似时与全等一样,要把表示对应顶点的字母写在对应的位置上.
相似比的概念:
相似多边形对应边的比叫作相似比,例如,五边形ABCDE∽五边形A1B1C1D1E1,对应边=====,因此五边形ABCDE与五边形A1B1C1D1E1的相似比为k1=,五边形A1B1C1D1E1与五边形ABCDE的相似比为k2=.
设计意图:从特例入手,学生比较容易接受,而从特例的探索过程得到的活动经验对一般情况的探索起到铺垫的作用,从而降低难度.
特殊的相似多边形的探究.
问题3:任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
师生活动:教师出示问题,学生思考、讨论,教师分析、引导.
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
思考:任意两个菱形相似吗?
任意两个菱形不一定相似,因为两个菱形的各边虽对应成比例,但它们的各角不一定分别对应相等.
设计意图:巩固对相似多边形概念的理解.
(三)典例解析
例1:一块长3 m、宽1.5 m的矩形黑板如图所示,镶在其外围的木质边框宽7.5cm.边框的内外边缘所成的矩形相似吗?为什么?
师生活动:教师出示问题,学生思考、讨论,教师引导学生应用相似多边形的定义判断.
答:不相似;因为,所以对应边不成比例.所以这两个矩形不相似.
设计意图:加深对相似多边形概念的理解.
例2:如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等,由此可得
α=∠C=83°,∠A=∠E=118°.
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
因为四边形ABCD和EFGH相似,
所以它们的对应边成比例,由此可得
,即.
解得x=28.
设计意图:通过求相似多边形的对应边、角,巩固相似多边形的概念及性质.
例3:如图,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴.
∴EF2=AD·BC=3×4=12,
∴EF=2.
∵四边形AEFD∽四边形EBCF,
∴AE:EB=AD:EF=3: 2=:2.
设计意图:通过例题,进一步巩固相似多边形和相似比的概念,让学生加强理解.
(四)课堂演练
1.下列命题中,正确的是( )
A.所有的等腰三角形都相似 B.所有的直角三角形都相似
C.所有的等边三角形都相似 D.所有的矩形都相似
2.若△ABC∽△ A′B′C′,且AB:A′B′=1:2
则△ABC与△ A′B′C′相似比是 ,△ A′B′C′与△ABC的相似比是 .
3. 如图所示的两个四边形是否相似?
4. 填空:
(1) 如图①是两个相似的四边形,则x= ,y = , α= ;
(2) 如图②是两个相似的矩形, x= .
设计意图:让学生自己小结,自己对本节课知识进行整合,培养学生养成一种对所学知识进行归纳总结的习惯.
(五)课堂小结
1.什么是相似多边形与相似比
2.怎么说明两个多边形是相似多边形
设计意图:让学生自己小结,自己对本节课知识进行整合,培养学生养成一种对所学知识进行归纳总结的习惯.
(六)布置作业
教材第88页习题4.4第1,2题.
五、板书设计
4.3 相似多边形
1.相似多边形及其相关概念
2.相似多边形的性质
3.典例解析
4.小结
六、教学反思
本节课的重点是相似多边形和相似比的概念和特征的学习,问题设计让学生参与到教学活动中,锻炼学生的观察、比较和归纳能力,并渗透类比的数学思想:让学生通过观察、猜想等方法,得出相似多边形的概念,帮助学生更加深入透彻地理解;最后通过一系列习题的演练,巩固所学知识,提高辨认图形的能力,为后续课程的学习打下基础.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
