初中数学北师大版九年级上4.8.1图形的位似 教学设计
文档属性
| 名称 | 初中数学北师大版九年级上4.8.1图形的位似 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:16:40 | ||
图片预览

文档简介
4.8.1图形的位似
一、教学目标
1.了解位似多边形及其有关概念,了解位似与相似的联系和区别;
2.掌握位似图形的性质,会画位似图形;
3.会利用位似将一个图形放大或缩小.
二、教学重难点
重点:位似图形的定义、性质与作图;利用位似将一个图形放大或缩小.
难点:将放大或缩小的图形与原图形进行比较,归纳位似放大或缩小图形的规律.
三、教学方法
从学生生活经验和已有的知识出发,采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习;提高学生自主探究、合作交流和分析归纳能力;同时在教学过程对不同层次的学生进行分类指导,让每个学生都得到充分的发展.
四、教学设计
(一)复习回顾
1. 前面我们已经学习了图形的哪些变换?
平移,轴对称,旋转.
图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
问题2:如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
师生活动:教师出示问题,学生思考、讨论并回答问题.
设计意图:展示生活中的位似图片,让学生体会学习本节课的价值,激发学生的学习兴趣.
(二)问题探究
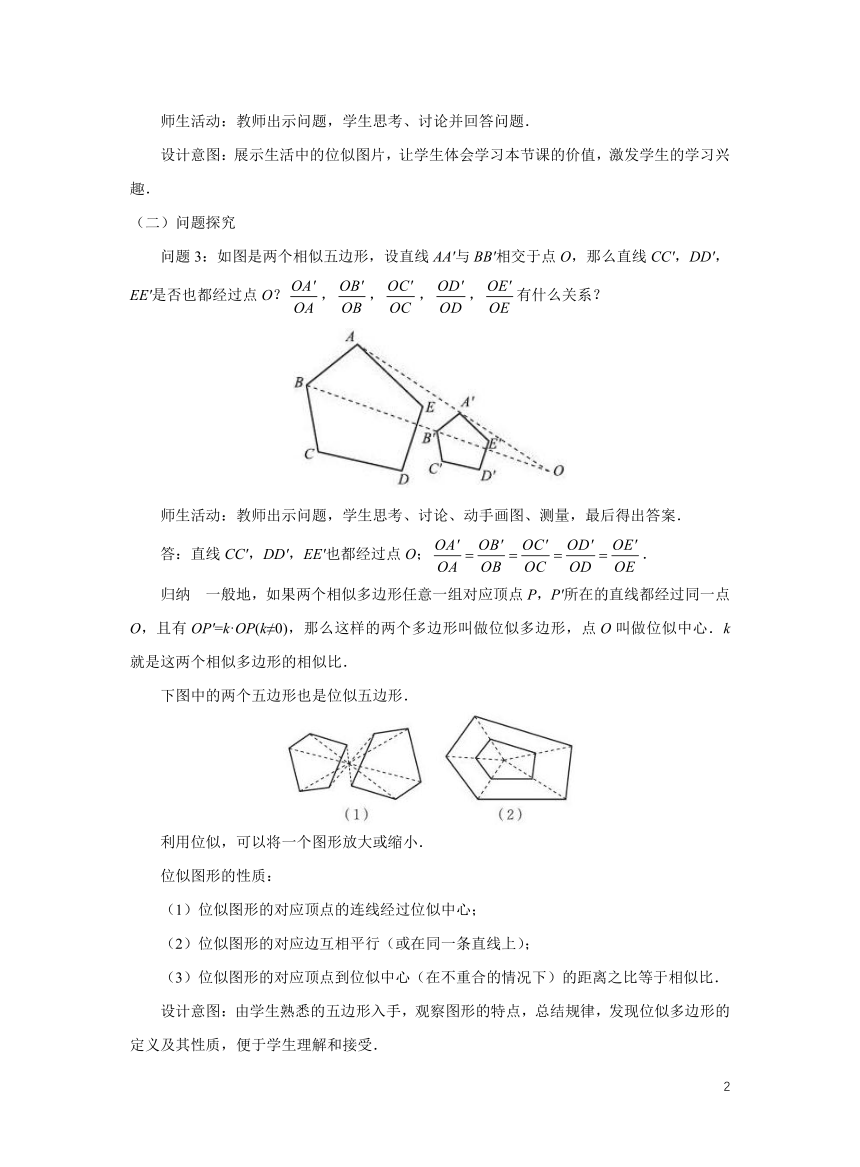
问题3:如图是两个相似五边形,设直线AA'与BB'相交于点O,那么直线CC',DD',EE'是否也都经过点O?,,,,有什么关系?
师生活动:教师出示问题,学生思考、讨论、动手画图、测量,最后得出答案.
答:直线CC',DD',EE'也都经过点O;.
归纳 一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.k就是这两个相似多边形的相似比.
下图中的两个五边形也是位似五边形.
利用位似,可以将一个图形放大或缩小.
位似图形的性质:
(1)位似图形的对应顶点的连线经过位似中心;
(2)位似图形的对应边互相平行(或在同一条直线上);
(3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比.
设计意图:由学生熟悉的五边形入手,观察图形的特点,总结规律,发现位似多边形的定义及其性质,便于学生理解和接受.
(三)典例解析
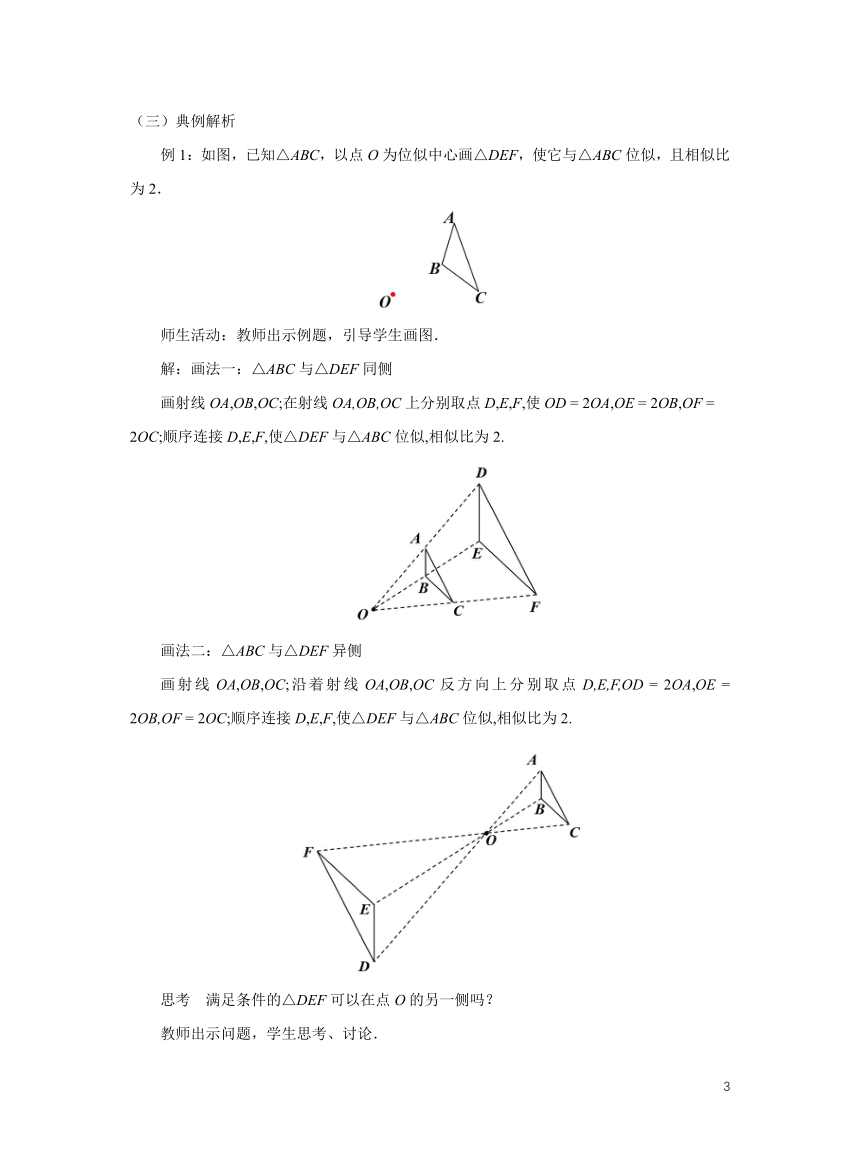
例1:如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
师生活动:教师出示例题,引导学生画图.
解:画法一:△ABC与△DEF同侧
画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD = 2OA,OE = 2OB,OF = 2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
画法二:△ABC与△DEF异侧
画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD = 2OA,OE = 2OB,OF = 2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
思考 满足条件的△DEF可以在点O的另一侧吗?
教师出示问题,学生思考、讨论.
答:满足条件的△DEF可以在点O的另一侧.
设计意图:让学生亲自操作、画图,组内交流,研究解决问题的方法,使其对新知识的把握更准确到位,让学生在数学学习的过程中,体验获得成功的乐趣,在探索过程中体会分类讨论的数学思想.
例2:已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
画法一:△ABC与△DEF在同侧
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
画法二: △ABC与△DEF在异侧
解:画射线OA,OB,OC;在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
总结:
(1)画位似图形时,要注意相似比,即分清楚是已知原图与新图的相似比,还是新图与原图的相似比.
(2)画位似图形的关键是画出图形中顶点的对应点.画图的方法大致有两种:一是每对对应点都在位似中心的同侧;二是每对对应点都在位似中心的两侧.
(3)若没有指定位似中心的位置,则画图时位似中心的取法有多种.
利用下面的方法可以近似地将一个图形放大:
(1)将两根长短相同的橡皮筋系在一起,联结处形成一个结点;
(2)选取一个图形,在图形外取一个定点;
(3)将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端;
(4)拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形.
(四)课堂演练
1. 选出下面不同于其他三组的图形 ( )
2.下列关于位似图形的三个表述中正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形.
A.0个 B.1个 C.2个 D.3个
3. 下列说法:
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且位似比相等. 其中正确的有 .
设计意图:进一步巩固所学知识,加深对所学知识的理解.
(五)课堂小结
1.位似多边形的概念
一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.k就是这两个相似多边形的相似比.
2.位似图形的性质
(1)位似图形的对应顶点的连线经过位似中心;
(2)位似图形的对应边互相平行(或在同一条直线上);
(3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比. 师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:帮助学生养成系统整理知识的学习习惯,加深认识,深化提高,形成学生自己的知识体系.
(六)布置作业
教材第115页习题4.13.
五、板书设计
4.8.1 图形的位似
1.位似多边形的概念;
2.位似图形的性质;
3.作图;
4.小结.
六、教学反思
位似是相似图形的延伸和深化.经历位似图形的探索过程,进一步发展学生的探究、交流能力,培养学生动手操作的能力,体验学习的乐趣.位似图形在实际生产和生活中有着广泛的应用,通过现实情境,进一步发展学生从数学角度提出问题、分析问题、解决问题的能力,培养学生的数学应用意识,体会数学与自然、社会的联系.
1
一、教学目标
1.了解位似多边形及其有关概念,了解位似与相似的联系和区别;
2.掌握位似图形的性质,会画位似图形;
3.会利用位似将一个图形放大或缩小.
二、教学重难点
重点:位似图形的定义、性质与作图;利用位似将一个图形放大或缩小.
难点:将放大或缩小的图形与原图形进行比较,归纳位似放大或缩小图形的规律.
三、教学方法
从学生生活经验和已有的知识出发,采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习;提高学生自主探究、合作交流和分析归纳能力;同时在教学过程对不同层次的学生进行分类指导,让每个学生都得到充分的发展.
四、教学设计
(一)复习回顾
1. 前面我们已经学习了图形的哪些变换?
平移,轴对称,旋转.
图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
问题2:如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
师生活动:教师出示问题,学生思考、讨论并回答问题.
设计意图:展示生活中的位似图片,让学生体会学习本节课的价值,激发学生的学习兴趣.
(二)问题探究
问题3:如图是两个相似五边形,设直线AA'与BB'相交于点O,那么直线CC',DD',EE'是否也都经过点O?,,,,有什么关系?
师生活动:教师出示问题,学生思考、讨论、动手画图、测量,最后得出答案.
答:直线CC',DD',EE'也都经过点O;.
归纳 一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.k就是这两个相似多边形的相似比.
下图中的两个五边形也是位似五边形.
利用位似,可以将一个图形放大或缩小.
位似图形的性质:
(1)位似图形的对应顶点的连线经过位似中心;
(2)位似图形的对应边互相平行(或在同一条直线上);
(3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比.
设计意图:由学生熟悉的五边形入手,观察图形的特点,总结规律,发现位似多边形的定义及其性质,便于学生理解和接受.
(三)典例解析
例1:如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且相似比为2.
师生活动:教师出示例题,引导学生画图.
解:画法一:△ABC与△DEF同侧
画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD = 2OA,OE = 2OB,OF = 2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
画法二:△ABC与△DEF异侧
画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD = 2OA,OE = 2OB,OF = 2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
思考 满足条件的△DEF可以在点O的另一侧吗?
教师出示问题,学生思考、讨论.
答:满足条件的△DEF可以在点O的另一侧.
设计意图:让学生亲自操作、画图,组内交流,研究解决问题的方法,使其对新知识的把握更准确到位,让学生在数学学习的过程中,体验获得成功的乐趣,在探索过程中体会分类讨论的数学思想.
例2:已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
画法一:△ABC与△DEF在同侧
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
画法二: △ABC与△DEF在异侧
解:画射线OA,OB,OC;在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;顺序连接D,E,F,使△DEF与△ABC位似,位似比为1:2.
总结:
(1)画位似图形时,要注意相似比,即分清楚是已知原图与新图的相似比,还是新图与原图的相似比.
(2)画位似图形的关键是画出图形中顶点的对应点.画图的方法大致有两种:一是每对对应点都在位似中心的同侧;二是每对对应点都在位似中心的两侧.
(3)若没有指定位似中心的位置,则画图时位似中心的取法有多种.
利用下面的方法可以近似地将一个图形放大:
(1)将两根长短相同的橡皮筋系在一起,联结处形成一个结点;
(2)选取一个图形,在图形外取一个定点;
(3)将系在一起的橡皮筋的一端固定在定点,把一支铅笔固定在橡皮筋的另一端;
(4)拉动铅笔,使两根橡皮筋的结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出了一个新的图形.
(四)课堂演练
1. 选出下面不同于其他三组的图形 ( )
2.下列关于位似图形的三个表述中正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形.
A.0个 B.1个 C.2个 D.3个
3. 下列说法:
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则其中 △ABC 与 △A′B′C′ 也是位似的,且位似比相等. 其中正确的有 .
设计意图:进一步巩固所学知识,加深对所学知识的理解.
(五)课堂小结
1.位似多边形的概念
一般地,如果两个相似多边形任意一组对应顶点P,P'所在的直线都经过同一点O,且有OP'=k·OP(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.k就是这两个相似多边形的相似比.
2.位似图形的性质
(1)位似图形的对应顶点的连线经过位似中心;
(2)位似图形的对应边互相平行(或在同一条直线上);
(3)位似图形的对应顶点到位似中心(在不重合的情况下)的距离之比等于相似比. 师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:帮助学生养成系统整理知识的学习习惯,加深认识,深化提高,形成学生自己的知识体系.
(六)布置作业
教材第115页习题4.13.
五、板书设计
4.8.1 图形的位似
1.位似多边形的概念;
2.位似图形的性质;
3.作图;
4.小结.
六、教学反思
位似是相似图形的延伸和深化.经历位似图形的探索过程,进一步发展学生的探究、交流能力,培养学生动手操作的能力,体验学习的乐趣.位似图形在实际生产和生活中有着广泛的应用,通过现实情境,进一步发展学生从数学角度提出问题、分析问题、解决问题的能力,培养学生的数学应用意识,体会数学与自然、社会的联系.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
