初中数学北师大版九上5.2.2视图教学设计
文档属性
| 名称 | 初中数学北师大版九上5.2.2视图教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览

文档简介
5.2.2视图
一、教学目标
1.巩固视图及主视图、左视图、俯视图的概念.
2.会画直棱柱的三种视图,并能判定简单物体的视图.
3.经历有关视图的观察、操作、分析、抽象、概括、想象、推理、交流等过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念.
二、教学重难点
重点:会画三棱柱、四棱柱的三视图,能进行几何体和三视图之间的相互转化.
难点:明确三视图中实线和虚线的区别.
三、教学方法
本节课是在上节课的基础上进一步研究三视图的位置关系和大小关系,研究如何画出简单组合几何体的三视图,画几何体的三视图,本节课应继续注重培养学生的空间想象能力.
四、教学设计
(一)复习回顾
1.什么是视图?
用正投影的方法绘制的物体在投影面上的图形,称为物体的视图.
2.什么是三视图?
从正面得到的视图叫做主视图,
从左面得到的视图叫做左视图,
从上面得到的视图叫做俯视图.
设计意图:通过简单复习上节课所学内容,自然引入本节课所学内容.
(二)问题探究
问题1:如图是一个正三棱柱.
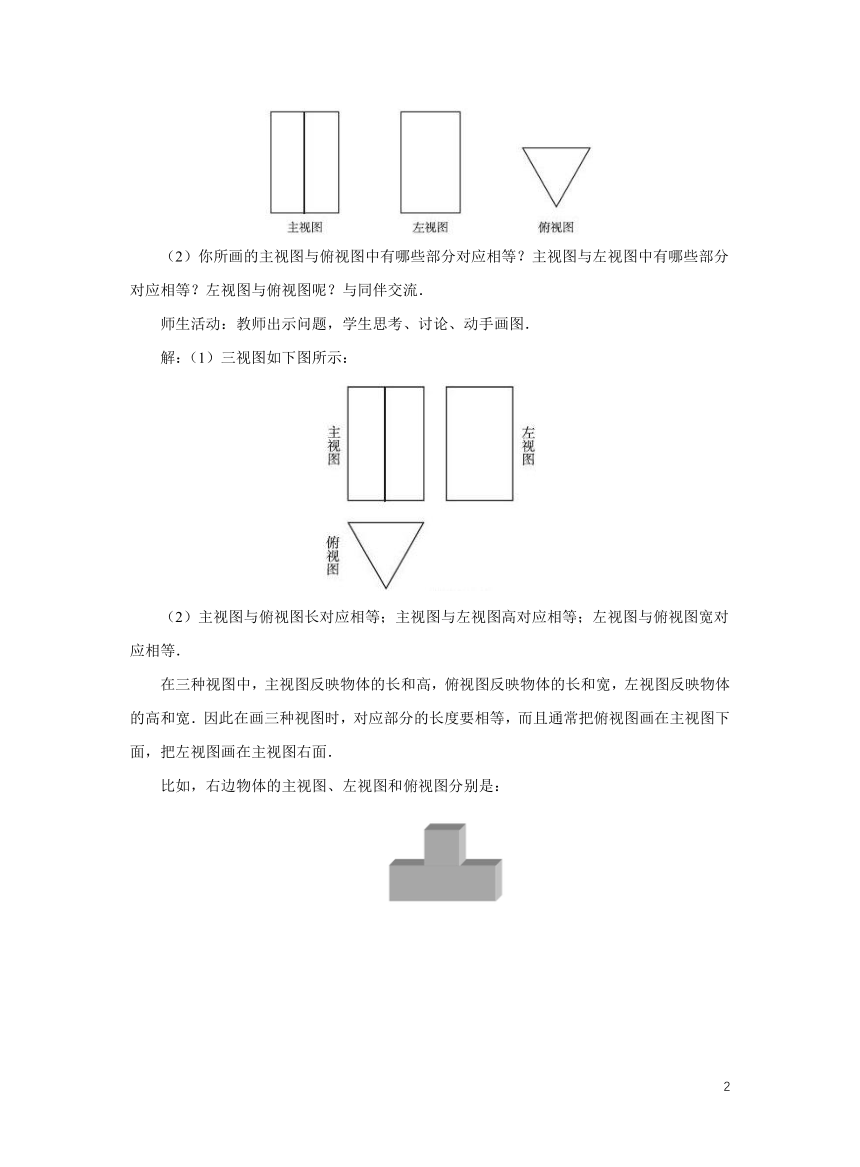
(1)你能想象出这个正三棱柱的主视图、左视图和俯视图吗?你能画出它们吗?
(2)你所画的主视图与俯视图中有哪些部分对应相等?主视图与左视图中有哪些部分对应相等?左视图与俯视图呢?与同伴交流.
师生活动:教师出示问题,学生思考、讨论、动手画图.
解:(1)三视图如下图所示:
(2)主视图与俯视图长对应相等;主视图与左视图高对应相等;左视图与俯视图宽对应相等.
在三种视图中,主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.因此在画三种视图时,对应部分的长度要相等,而且通常把俯视图画在主视图下面,把左视图画在主视图右面.
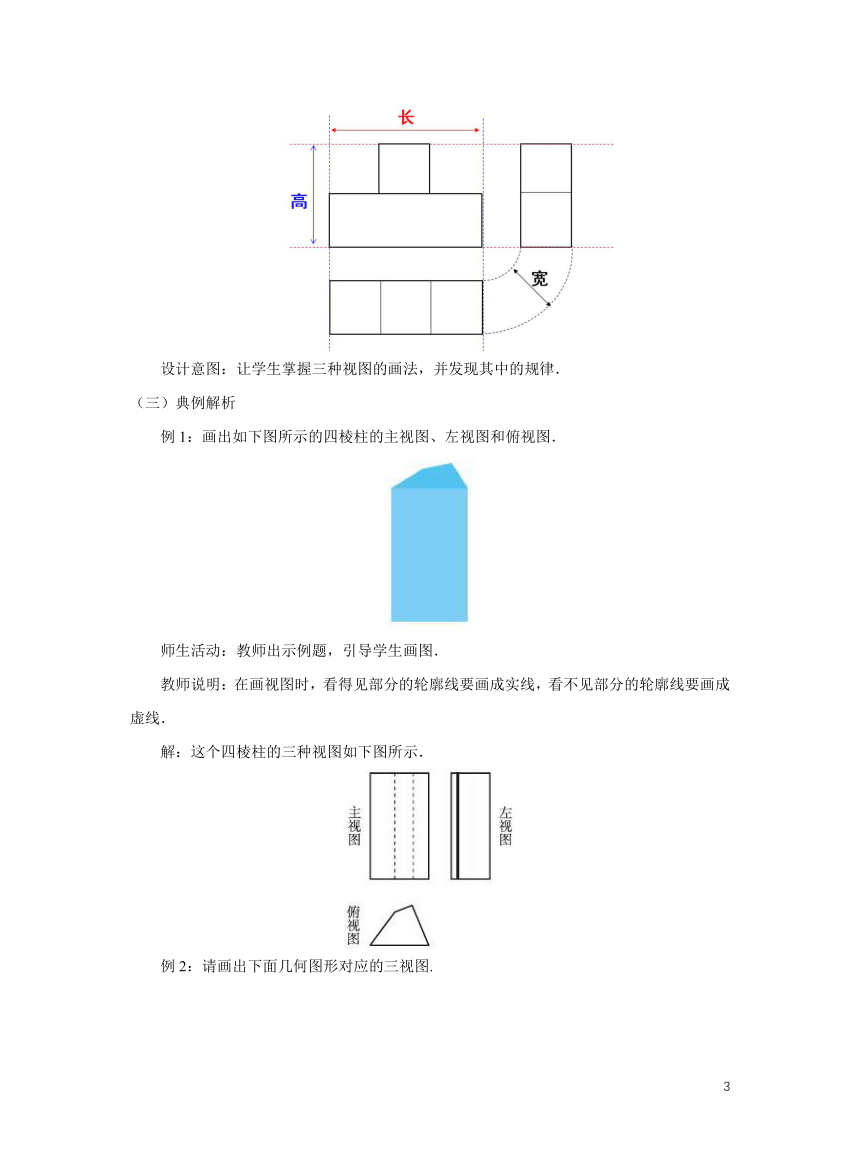
比如,右边物体的主视图、左视图和俯视图分别是:
设计意图:让学生掌握三种视图的画法,并发现其中的规律.
(三)典例解析
例1:画出如下图所示的四棱柱的主视图、左视图和俯视图.
师生活动:教师出示例题,引导学生画图.
教师说明:在画视图时,看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线.
解:这个四棱柱的三种视图如下图所示.
例2:请画出下面几何图形对应的三视图.
解:(1)
(2)
设计意图:让学生亲自操作、画图,组内交流,研究解决问题的方法,使其对新知识的把握更准确到位.
例3:两个三棱柱的底面均为等腰直角三角形,它们的俯视图分别如下图所示,画出它们的主视图和左视图.
解:图(1)中的主视图和左视图可以是:
图(2)中的主视图和左视图可以是:
(四)课堂演练
1.如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
A.俯视图与主视图相同
B.左视图与主视图相同
C.左视图与俯视图相同
D.三个视图都相同
2.一个圆柱体钢块,从正中间挖去一个长方体得到的零件毛坯的俯视图如图,其主视图是( )
3.画出如图所示几何体的主视图、左视图和俯视图.
4.一个几何体的主视图和左视图如图所示,请补画这个几何体的俯视图.
5.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(五)课堂小结
1.画三种视图时,要遵循的法则是什么?
答:(1)位置方面:一般先画主视图,再把左视图画在主视图的右面,把俯视图画在主视图的下面;
(2)主视图与俯视图长对应相等,主视图与左视图高对应相等,左视图与俯视图宽对应相等.
(3)虚实方面:在画图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线.
师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:帮助学生养成系统整理知识的学习习惯,加深认识,深化提高,形成学生自己的知识体系.
(六)布置作业
教材第140页习题5.4.
五、板书设计
5.2.2 视图
1.回顾三视图的概念;
2.三视图的画法;
3.小结.
六、教学反思
经历由直棱柱到其三种视图的转化过程,进一步发展空间观念,培养学生自主学习与合作学习相结合的学习方式.在应用数学解决生活中问题的过程中,品尝成功的喜悦,激发学生应用数学的热情.
1
一、教学目标
1.巩固视图及主视图、左视图、俯视图的概念.
2.会画直棱柱的三种视图,并能判定简单物体的视图.
3.经历有关视图的观察、操作、分析、抽象、概括、想象、推理、交流等过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念.
二、教学重难点
重点:会画三棱柱、四棱柱的三视图,能进行几何体和三视图之间的相互转化.
难点:明确三视图中实线和虚线的区别.
三、教学方法
本节课是在上节课的基础上进一步研究三视图的位置关系和大小关系,研究如何画出简单组合几何体的三视图,画几何体的三视图,本节课应继续注重培养学生的空间想象能力.
四、教学设计
(一)复习回顾
1.什么是视图?
用正投影的方法绘制的物体在投影面上的图形,称为物体的视图.
2.什么是三视图?
从正面得到的视图叫做主视图,
从左面得到的视图叫做左视图,
从上面得到的视图叫做俯视图.
设计意图:通过简单复习上节课所学内容,自然引入本节课所学内容.
(二)问题探究
问题1:如图是一个正三棱柱.
(1)你能想象出这个正三棱柱的主视图、左视图和俯视图吗?你能画出它们吗?
(2)你所画的主视图与俯视图中有哪些部分对应相等?主视图与左视图中有哪些部分对应相等?左视图与俯视图呢?与同伴交流.
师生活动:教师出示问题,学生思考、讨论、动手画图.
解:(1)三视图如下图所示:
(2)主视图与俯视图长对应相等;主视图与左视图高对应相等;左视图与俯视图宽对应相等.
在三种视图中,主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.因此在画三种视图时,对应部分的长度要相等,而且通常把俯视图画在主视图下面,把左视图画在主视图右面.
比如,右边物体的主视图、左视图和俯视图分别是:
设计意图:让学生掌握三种视图的画法,并发现其中的规律.
(三)典例解析
例1:画出如下图所示的四棱柱的主视图、左视图和俯视图.
师生活动:教师出示例题,引导学生画图.
教师说明:在画视图时,看得见部分的轮廓线要画成实线,看不见部分的轮廓线要画成虚线.
解:这个四棱柱的三种视图如下图所示.
例2:请画出下面几何图形对应的三视图.
解:(1)
(2)
设计意图:让学生亲自操作、画图,组内交流,研究解决问题的方法,使其对新知识的把握更准确到位.
例3:两个三棱柱的底面均为等腰直角三角形,它们的俯视图分别如下图所示,画出它们的主视图和左视图.
解:图(1)中的主视图和左视图可以是:
图(2)中的主视图和左视图可以是:
(四)课堂演练
1.如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
A.俯视图与主视图相同
B.左视图与主视图相同
C.左视图与俯视图相同
D.三个视图都相同
2.一个圆柱体钢块,从正中间挖去一个长方体得到的零件毛坯的俯视图如图,其主视图是( )
3.画出如图所示几何体的主视图、左视图和俯视图.
4.一个几何体的主视图和左视图如图所示,请补画这个几何体的俯视图.
5.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.
(五)课堂小结
1.画三种视图时,要遵循的法则是什么?
答:(1)位置方面:一般先画主视图,再把左视图画在主视图的右面,把俯视图画在主视图的下面;
(2)主视图与俯视图长对应相等,主视图与左视图高对应相等,左视图与俯视图宽对应相等.
(3)虚实方面:在画图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线.
师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:帮助学生养成系统整理知识的学习习惯,加深认识,深化提高,形成学生自己的知识体系.
(六)布置作业
教材第140页习题5.4.
五、板书设计
5.2.2 视图
1.回顾三视图的概念;
2.三视图的画法;
3.小结.
六、教学反思
经历由直棱柱到其三种视图的转化过程,进一步发展空间观念,培养学生自主学习与合作学习相结合的学习方式.在应用数学解决生活中问题的过程中,品尝成功的喜悦,激发学生应用数学的热情.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
