初中数学北师大版七上3.1字母表示数教学设计
文档属性
| 名称 | 初中数学北师大版七上3.1字母表示数教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 222.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览


文档简介
3.1字母表示数
一、教学目标
1.经历探索规律并用代数式表示规律的过程,感受从具体到抽象的思想.
2.能用字母表示运算律、计算公式以及一些简单问题中的数量关系和变化规律.
3.在具体情境中体会字母表示数的意义,形成初步的符号意识.
二、教学重难点
重点:理解字母表示数的意义,初步建立符号感,由特殊着手探究一般规律并用字母表示.
难点:探求如何用字母表示所探索的数的规律
三、教学过程
(一)情境导入
我们不少同学都是唱着儿歌长大的,朗朗上口、童趣横生的儿歌有的至今难以忘怀.其中有一首名叫《数蛤蟆》的儿歌,你想起来了吗?
一只青蛙一张嘴,两只眼睛四条腿,扑通一声跳下水;两只青蛙两张嘴,四只眼睛八条腿,扑通两声跳下水;三只青蛙三张嘴,六只眼睛……;m只青蛙m张嘴,2m只眼睛4m条腿.由此看出m是一个字母,它代表“很多只”的数量.用字母m可以清楚地表示出青蛙、嘴、眼睛、腿和跳水声之间的数量关系.
今天我们就学习用字母表示数.
(二)问题探究
问题1:如图:搭一个正方形需要4根火柴棒,那么:
(1)搭2个正方形需要____根火柴棒;3个正方形需要____根火柴棒;搭10个正方形需要____个火柴捧.
(2)如要搭n个正方形,则需要的火柴棒是_____根,你有几种方法可以得到这个结果?
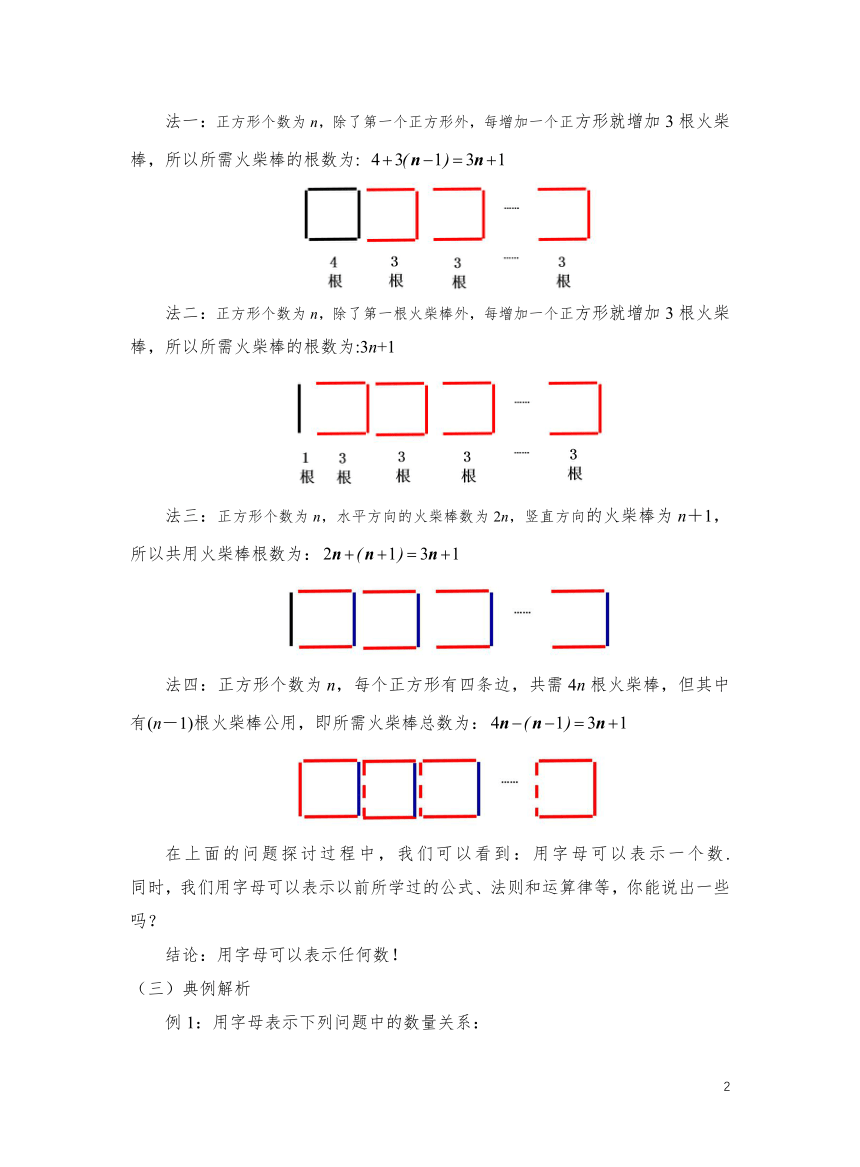
法一:正方形个数为n,除了第一个正方形外,每增加一个正方形就增加3根火柴棒,所以所需火柴棒的根数为:
法二:正方形个数为n,除了第一根火柴棒外,每增加一个正方形就增加3根火柴棒,所以所需火柴棒的根数为:3n+1
法三:正方形个数为n,水平方向的火柴棒数为2n,竖直方向的火柴棒为n+1,所以共用火柴棒根数为:
法四:正方形个数为n,每个正方形有四条边,共需4n根火柴棒,但其中有(n-1)根火柴棒公用,即所需火柴棒总数为:
在上面的问题探讨过程中,我们可以看到:用字母可以表示一个数. 同时,我们用字母可以表示以前所学过的公式、法则和运算律等,你能说出一些吗?
结论:用字母可以表示任何数!
(三)典例解析
例1:用字母表示下列问题中的数量关系:
(1)为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为 元;
(2)在运动会中,一班总成绩为m分,二班比一班总成绩的还多5分,则二班的总成绩为 ;
(3)某商店压了一批商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元.
(1)(80m+60n)(2)(3)0.945m
例2:用字母表示图中阴影部分的面积:
(1) (2)
解析:(1)图中阴影部分的面积是正方形中挖去一个圆后剩下的部分,且正方形的边长是a,圆的直径也是a,则圆的半径是;(2)图中阴影部分是长方形中挖去4个小正方形后剩下的部分,且长方形的长为a,宽为b,小正方形的边长为x.
解:(1)S=a2-π·()2;(2)S=ab-4x2.
方法总结:将不规则图形的面积转化为规则图形(如长方形、圆、三角形等)的面积的和或差是解决求阴影部分面积问题的关键.
例3:如图是一组有规律的图案,第一个图案由4个▲组成,第二个图案由7个▲组成,第三个图案由10个▲组成,第四个图案由13个▲组成,……,则第n(n为正整数)个图案由 个▲组成.
解析:第一个图案由4个▲组成,即4=3×1+1;第二个图案由7个▲组成,即7=3×2+1;第三个图案由10个▲组成,即10=3×3+1,……,由此可知,第n个图案由(3n+1)个▲组成.故填(3n+1).
方法总结:规律的探索往往要经历从特殊(具体实例)到一般(用字母表示)再到特殊(验证)的过程.
(四)知识要点
知识点一:用字母表示数
(1)用字母表示数,字母和数一样可以参与_______,可以用式子把________关系简明的表示出来.
(2)含字母式子的书写规范:
(3)注意:
①数与数相乘时,仍要用“×”.
②同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的_______表示.
③代数式后面有单位时,和、差形式的代数式要在单位前把代数式括起来.
知识点二:用字母表示运算律和公式
(1)用字母表示运算律:
如:加法交换律:a+b=b+a;
乘法交换律:ab=ba;
加法结合律:(a+b)+c=a+(b+c).
(2)用字母表示公式:
用字母不仅可以表示运算律,还可以表示生活中的实际数量关系,如:若用s表示路程,用t表示时间,用v表示速度,则有s=vt.
(五)课堂演练
1.(1)书写规范下列的式子:
①m×(7)=_7m____;
②2×a=___a___;
③a÷b=_____.
(2)一件衣服的原价为m元,按7折优惠出售,则售价为_0.7m__元.
(3)下列含有字母的式子中,书写规范的是( C )
A.1m B.8n C.ab D.(xy)÷z
2.(1)棱长是a cm的正方体的体积是__a3___cm3;
(2)如果手机通话每分钟收费m元,那么通话n分钟收费_mn___元;
(3)端午节期间,“惠民超市”销售的粽子打8折后卖a元,则粽子的原价卖___a___元.
3. 有一个两位数,它的十位数字是a,个位数字是b,则这个两位数可以表示为( C )
A.a+b B.a×b C.10a+b D.10(a+b)
4. 如图,图中阴影部分的面积表示为___mnpq______.
5.如图,图中阴影部分的面积可以用字母表示为____πR2R2______.
(四)课堂小结
通过这节课的学习,同学们的学习态度让老师满意,请同学们谈谈这节课的收获和感受
(五)布置作业
教材习题3.1第2-3题.
四、板书设计
五、教学反思
通过本课时的教学要让学生经历在实际问题中用字母表示数,初步理解用字母表示数的意义及目的,让学生循序渐进的学习本部分内容,可以先用数,后用字母来表示.让学生在现实情境中去理解、感悟、体会字母能够代替数,发展学生的符号感.在数学教学中,让学生逐步学会用代数的思想方法分析和解决问题,体会其优越性,让学生体验成就感.
1
一、教学目标
1.经历探索规律并用代数式表示规律的过程,感受从具体到抽象的思想.
2.能用字母表示运算律、计算公式以及一些简单问题中的数量关系和变化规律.
3.在具体情境中体会字母表示数的意义,形成初步的符号意识.
二、教学重难点
重点:理解字母表示数的意义,初步建立符号感,由特殊着手探究一般规律并用字母表示.
难点:探求如何用字母表示所探索的数的规律
三、教学过程
(一)情境导入
我们不少同学都是唱着儿歌长大的,朗朗上口、童趣横生的儿歌有的至今难以忘怀.其中有一首名叫《数蛤蟆》的儿歌,你想起来了吗?
一只青蛙一张嘴,两只眼睛四条腿,扑通一声跳下水;两只青蛙两张嘴,四只眼睛八条腿,扑通两声跳下水;三只青蛙三张嘴,六只眼睛……;m只青蛙m张嘴,2m只眼睛4m条腿.由此看出m是一个字母,它代表“很多只”的数量.用字母m可以清楚地表示出青蛙、嘴、眼睛、腿和跳水声之间的数量关系.
今天我们就学习用字母表示数.
(二)问题探究
问题1:如图:搭一个正方形需要4根火柴棒,那么:
(1)搭2个正方形需要____根火柴棒;3个正方形需要____根火柴棒;搭10个正方形需要____个火柴捧.
(2)如要搭n个正方形,则需要的火柴棒是_____根,你有几种方法可以得到这个结果?
法一:正方形个数为n,除了第一个正方形外,每增加一个正方形就增加3根火柴棒,所以所需火柴棒的根数为:
法二:正方形个数为n,除了第一根火柴棒外,每增加一个正方形就增加3根火柴棒,所以所需火柴棒的根数为:3n+1
法三:正方形个数为n,水平方向的火柴棒数为2n,竖直方向的火柴棒为n+1,所以共用火柴棒根数为:
法四:正方形个数为n,每个正方形有四条边,共需4n根火柴棒,但其中有(n-1)根火柴棒公用,即所需火柴棒总数为:
在上面的问题探讨过程中,我们可以看到:用字母可以表示一个数. 同时,我们用字母可以表示以前所学过的公式、法则和运算律等,你能说出一些吗?
结论:用字母可以表示任何数!
(三)典例解析
例1:用字母表示下列问题中的数量关系:
(1)为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为 元;
(2)在运动会中,一班总成绩为m分,二班比一班总成绩的还多5分,则二班的总成绩为 ;
(3)某商店压了一批商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元.
(1)(80m+60n)(2)(3)0.945m
例2:用字母表示图中阴影部分的面积:
(1) (2)
解析:(1)图中阴影部分的面积是正方形中挖去一个圆后剩下的部分,且正方形的边长是a,圆的直径也是a,则圆的半径是;(2)图中阴影部分是长方形中挖去4个小正方形后剩下的部分,且长方形的长为a,宽为b,小正方形的边长为x.
解:(1)S=a2-π·()2;(2)S=ab-4x2.
方法总结:将不规则图形的面积转化为规则图形(如长方形、圆、三角形等)的面积的和或差是解决求阴影部分面积问题的关键.
例3:如图是一组有规律的图案,第一个图案由4个▲组成,第二个图案由7个▲组成,第三个图案由10个▲组成,第四个图案由13个▲组成,……,则第n(n为正整数)个图案由 个▲组成.
解析:第一个图案由4个▲组成,即4=3×1+1;第二个图案由7个▲组成,即7=3×2+1;第三个图案由10个▲组成,即10=3×3+1,……,由此可知,第n个图案由(3n+1)个▲组成.故填(3n+1).
方法总结:规律的探索往往要经历从特殊(具体实例)到一般(用字母表示)再到特殊(验证)的过程.
(四)知识要点
知识点一:用字母表示数
(1)用字母表示数,字母和数一样可以参与_______,可以用式子把________关系简明的表示出来.
(2)含字母式子的书写规范:
(3)注意:
①数与数相乘时,仍要用“×”.
②同一问题中,相同的字母必须表示相同的量,不同的量必须用不同的_______表示.
③代数式后面有单位时,和、差形式的代数式要在单位前把代数式括起来.
知识点二:用字母表示运算律和公式
(1)用字母表示运算律:
如:加法交换律:a+b=b+a;
乘法交换律:ab=ba;
加法结合律:(a+b)+c=a+(b+c).
(2)用字母表示公式:
用字母不仅可以表示运算律,还可以表示生活中的实际数量关系,如:若用s表示路程,用t表示时间,用v表示速度,则有s=vt.
(五)课堂演练
1.(1)书写规范下列的式子:
①m×(7)=_7m____;
②2×a=___a___;
③a÷b=_____.
(2)一件衣服的原价为m元,按7折优惠出售,则售价为_0.7m__元.
(3)下列含有字母的式子中,书写规范的是( C )
A.1m B.8n C.ab D.(xy)÷z
2.(1)棱长是a cm的正方体的体积是__a3___cm3;
(2)如果手机通话每分钟收费m元,那么通话n分钟收费_mn___元;
(3)端午节期间,“惠民超市”销售的粽子打8折后卖a元,则粽子的原价卖___a___元.
3. 有一个两位数,它的十位数字是a,个位数字是b,则这个两位数可以表示为( C )
A.a+b B.a×b C.10a+b D.10(a+b)
4. 如图,图中阴影部分的面积表示为___mnpq______.
5.如图,图中阴影部分的面积可以用字母表示为____πR2R2______.
(四)课堂小结
通过这节课的学习,同学们的学习态度让老师满意,请同学们谈谈这节课的收获和感受
(五)布置作业
教材习题3.1第2-3题.
四、板书设计
五、教学反思
通过本课时的教学要让学生经历在实际问题中用字母表示数,初步理解用字母表示数的意义及目的,让学生循序渐进的学习本部分内容,可以先用数,后用字母来表示.让学生在现实情境中去理解、感悟、体会字母能够代替数,发展学生的符号感.在数学教学中,让学生逐步学会用代数的思想方法分析和解决问题,体会其优越性,让学生体验成就感.
1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
