初中数学北师大版九上1.3.1正方形的性质与判定教学设计
文档属性
| 名称 | 初中数学北师大版九上1.3.1正方形的性质与判定教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 46.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:46:30 | ||
图片预览

文档简介
1.3.1正方形的性质与判定
一、教学目标
1.了解正方形的有关概念,理解并掌握正方形的性质定理;
2.会利用正方形的性质进行相关的计算和证明.
二、教学重难点
重点:理解正方形的定义和性质.
难点:灵活地运用正方形的性质定理解决问题.
三、教学设计
(一)情境导入
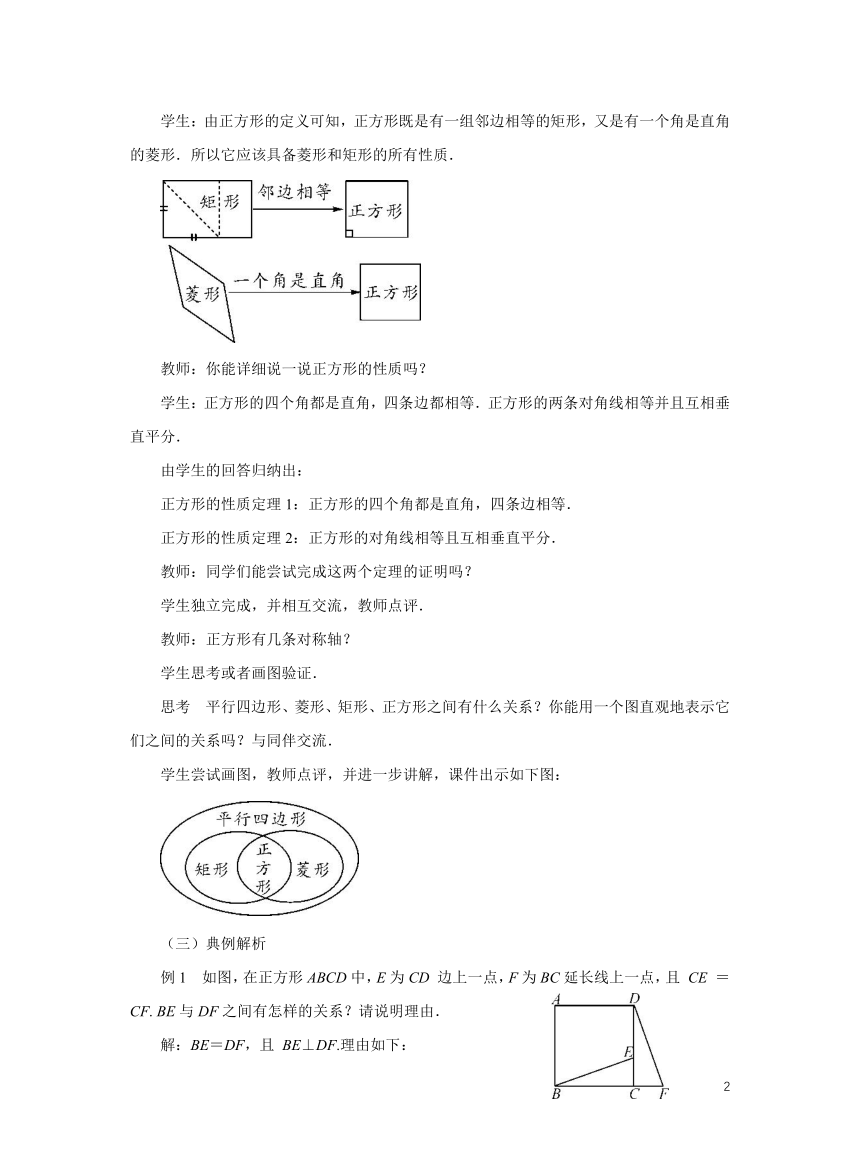
如图(1)所示,把可以活动的矩形框架ABCD的BC边平行移动,使矩形的邻边AD,DC相等,观察这时矩形ABCD的形状.
如图(2)所示,把可以活动的菱形框架ABCD的∠A变为直角,观察这时菱形ABCD的形状.
图(1)中图形的变化可判断矩形ABCD→特殊的四边形是什么四边形?图(2)中图形变化可判断菱形ABCD→特殊的四边形是什么四边形?经过观察,你发现既是矩形又是菱形的图形是什么四边形?
引入正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
注意:正方形既是特殊的矩形,又是特殊的菱形,即:有一组邻边相等的矩形是正方形或有一个角是直角的菱形是正方形.
(二)探究新知
教师:正方形都具有哪些性质呢?
学生:由正方形的定义可知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.所以它应该具备菱形和矩形的所有性质.
教师:你能详细说一说正方形的性质吗?
学生:正方形的四个角都是直角,四条边都相等.正方形的两条对角线相等并且互相垂直平分.
由学生的回答归纳出:
正方形的性质定理1:正方形的四个角都是直角,四条边相等.
正方形的性质定理2:正方形的对角线相等且互相垂直平分.
教师:同学们能尝试完成这两个定理的证明吗?
学生独立完成,并相互交流,教师点评.
教师:正方形有几条对称轴?
学生思考或者画图验证.
思考 平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.
学生尝试画图,教师点评,并进一步讲解,课件出示如下图:
(三)典例解析
例1 如图,在正方形ABCD中,E为CD 边上一点,F为BC延长线上一点,且 CE = CF. BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且 BE⊥DF.理由如下:
(1)∵ 四边形 ABCD 是正方形,
∴ BC=DC,∠ BCE=90°(正方形的四条边相等,四个角都是直角).
∴ ∠ DCF = 180°- ∠ BCE = 180°- 90°= 90°.
∴ ∠BCE =∠ DCF.
又∵ CE=CF,
∴ △BCE≌△DCF.
∴ BE=DF.
(2)延长 BE交DF于点M(如图).
∵ △BCE ≌△DCF,
∴ ∠CBE=∠CDF.
∵ ∠DCF=90°,
∴ ∠CDF+∠F=90°.
∴ ∠CBE+∠F=90°.
∴ ∠BMF=90°.
∴ BE⊥DF.
例2 如图,在正方形ABCD中, △BEC是等边三角形, 求证:∠EAD=∠EDA=15° .
证明:∵△BEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
例3 如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
证明:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC , PF⊥DC,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=EF.
(四)巩固提升
1.如图,在正方形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形?
第1题图 第2题图
如图,在正方形ABCD中,点F为对角线BD上一点,连接AF,CF. 你能找出图中的全等三角形吗?选择其中一对进行证明.
补充练习见课件
(五)课堂小结
通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?
(六)课外作业
教材第22页习题1.7第1~4题.
四、板书设计
正方形
五、教学反思
本节课教学的主要内容是探究并证明正方形的性质定理.教材只是提供了最基本的教学素材,教师完全可以根据学生的实际情况进行适当调整.让学生通过搜集材料亲自去感受数学在实际生活中的应用,体会数学的实际价值.培养学生善于观察生活、搜集数学信息、对信息进行整理的能力.
1
一、教学目标
1.了解正方形的有关概念,理解并掌握正方形的性质定理;
2.会利用正方形的性质进行相关的计算和证明.
二、教学重难点
重点:理解正方形的定义和性质.
难点:灵活地运用正方形的性质定理解决问题.
三、教学设计
(一)情境导入
如图(1)所示,把可以活动的矩形框架ABCD的BC边平行移动,使矩形的邻边AD,DC相等,观察这时矩形ABCD的形状.
如图(2)所示,把可以活动的菱形框架ABCD的∠A变为直角,观察这时菱形ABCD的形状.
图(1)中图形的变化可判断矩形ABCD→特殊的四边形是什么四边形?图(2)中图形变化可判断菱形ABCD→特殊的四边形是什么四边形?经过观察,你发现既是矩形又是菱形的图形是什么四边形?
引入正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
注意:正方形既是特殊的矩形,又是特殊的菱形,即:有一组邻边相等的矩形是正方形或有一个角是直角的菱形是正方形.
(二)探究新知
教师:正方形都具有哪些性质呢?
学生:由正方形的定义可知,正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形.所以它应该具备菱形和矩形的所有性质.
教师:你能详细说一说正方形的性质吗?
学生:正方形的四个角都是直角,四条边都相等.正方形的两条对角线相等并且互相垂直平分.
由学生的回答归纳出:
正方形的性质定理1:正方形的四个角都是直角,四条边相等.
正方形的性质定理2:正方形的对角线相等且互相垂直平分.
教师:同学们能尝试完成这两个定理的证明吗?
学生独立完成,并相互交流,教师点评.
教师:正方形有几条对称轴?
学生思考或者画图验证.
思考 平行四边形、菱形、矩形、正方形之间有什么关系?你能用一个图直观地表示它们之间的关系吗?与同伴交流.
学生尝试画图,教师点评,并进一步讲解,课件出示如下图:
(三)典例解析
例1 如图,在正方形ABCD中,E为CD 边上一点,F为BC延长线上一点,且 CE = CF. BE与DF之间有怎样的关系?请说明理由.
解:BE=DF,且 BE⊥DF.理由如下:
(1)∵ 四边形 ABCD 是正方形,
∴ BC=DC,∠ BCE=90°(正方形的四条边相等,四个角都是直角).
∴ ∠ DCF = 180°- ∠ BCE = 180°- 90°= 90°.
∴ ∠BCE =∠ DCF.
又∵ CE=CF,
∴ △BCE≌△DCF.
∴ BE=DF.
(2)延长 BE交DF于点M(如图).
∵ △BCE ≌△DCF,
∴ ∠CBE=∠CDF.
∵ ∠DCF=90°,
∴ ∠CDF+∠F=90°.
∴ ∠CBE+∠F=90°.
∴ ∠BMF=90°.
∴ BE⊥DF.
例2 如图,在正方形ABCD中, △BEC是等边三角形, 求证:∠EAD=∠EDA=15° .
证明:∵△BEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
例3 如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
证明:连接PC,AC.
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴AP=PC.
又∵PE⊥BC , PF⊥DC,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=EF.
(四)巩固提升
1.如图,在正方形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形?
第1题图 第2题图
如图,在正方形ABCD中,点F为对角线BD上一点,连接AF,CF. 你能找出图中的全等三角形吗?选择其中一对进行证明.
补充练习见课件
(五)课堂小结
通过这节课的学习,你有哪些收获?有何感想?学会了哪些方法?
(六)课外作业
教材第22页习题1.7第1~4题.
四、板书设计
正方形
五、教学反思
本节课教学的主要内容是探究并证明正方形的性质定理.教材只是提供了最基本的教学素材,教师完全可以根据学生的实际情况进行适当调整.让学生通过搜集材料亲自去感受数学在实际生活中的应用,体会数学的实际价值.培养学生善于观察生活、搜集数学信息、对信息进行整理的能力.
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
