28.1.3.锐角三角函数3(浙江省台州市)
文档属性
| 名称 | 28.1.3.锐角三角函数3(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-03 00:00:00 | ||
图片预览




文档简介
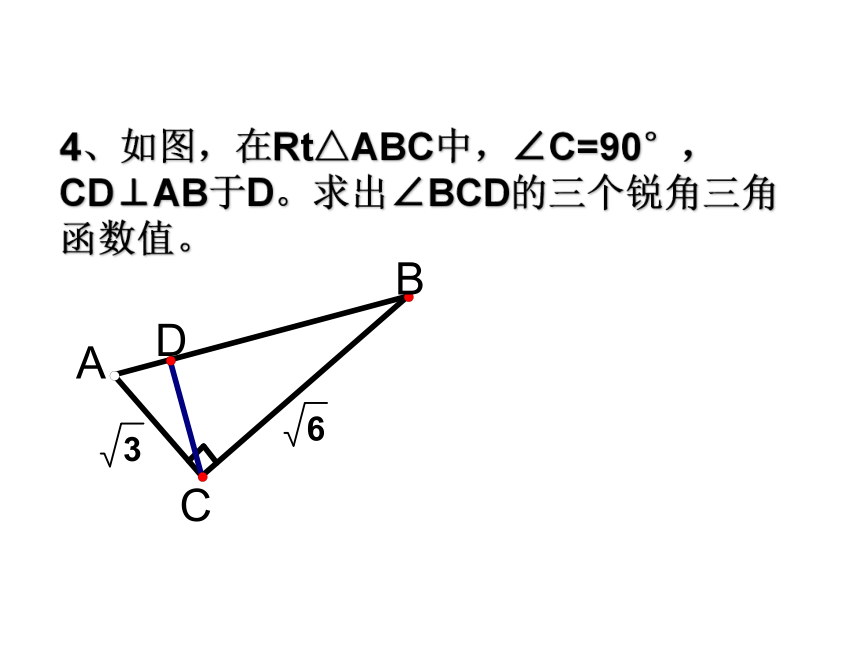
课件10张PPT。28.1.3 锐角三角函数(3)1.复习: 锐角三角函数的定义 在 中, ∠A的正弦: 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。 对于锐角A的每一个确定的值,sinA有唯一的值与它对应,所以sinA是A的函数。同样地,cosA、tanA也是A的函数。2.应用举例1、在Rt △ABC中,∠C=90°,求∠A的三角函数值。① a=9 b=12② a=9 c=12 2、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。 3、已知∠A为锐角,sinA= ,求cosA、tanA的值。4、如图,在Rt△ABC中,∠C=90°,CD⊥AB于D。求出∠BCD的三个锐角三角函数值。若已知锐角α的始边在x轴的正半轴上,(顶点在原点)
终边上一点P的坐标为(x, y),它到原点的距离为r
求角α的四个三角函数值。3.成果推广sinα= ,
cosα= ,
tanα= ,
cotα= .M拓广探索在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90°(1)用含a,b,c的代数式分别表示∠A,∠B的正弦和余弦.观察所得结果,你发现了什么?(2)用含a,b,的代数式分别表示∠A,∠B
的正切.观察所得结果,你发现了什么?在Rt△ABC中 及时总结经验,要养成积累方法和经验的良好习惯! 定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 再见
终边上一点P的坐标为(x, y),它到原点的距离为r
求角α的四个三角函数值。3.成果推广sinα= ,
cosα= ,
tanα= ,
cotα= .M拓广探索在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90°(1)用含a,b,c的代数式分别表示∠A,∠B的正弦和余弦.观察所得结果,你发现了什么?(2)用含a,b,的代数式分别表示∠A,∠B
的正切.观察所得结果,你发现了什么?在Rt△ABC中 及时总结经验,要养成积累方法和经验的良好习惯! 定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 再见
