2024北师版高中数学必修第二册同步练习题--专题强化练8 空间中的平行关系(含解析)
文档属性
| 名称 | 2024北师版高中数学必修第二册同步练习题--专题强化练8 空间中的平行关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 20:56:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024北师版高中数学必修第二册同步练习题
专题强化练8 空间中的平行关系
1.(2023河南新乡模拟)如图所示,在正方体或正三棱柱中,M,N,Q分别是所在棱的中点,则满足直线BM与平面CNQ平行的是( )
A B
C D
2.(2023新疆乌鲁木齐模拟)如图,在长方体ABCD-A1B1C1D1中,=2,则下列说法错误的是( )
A.BD1∥GH
B.BD与EF异面
C.EH∥平面ABCD
D.平面EFGH∥平面A1BCD1
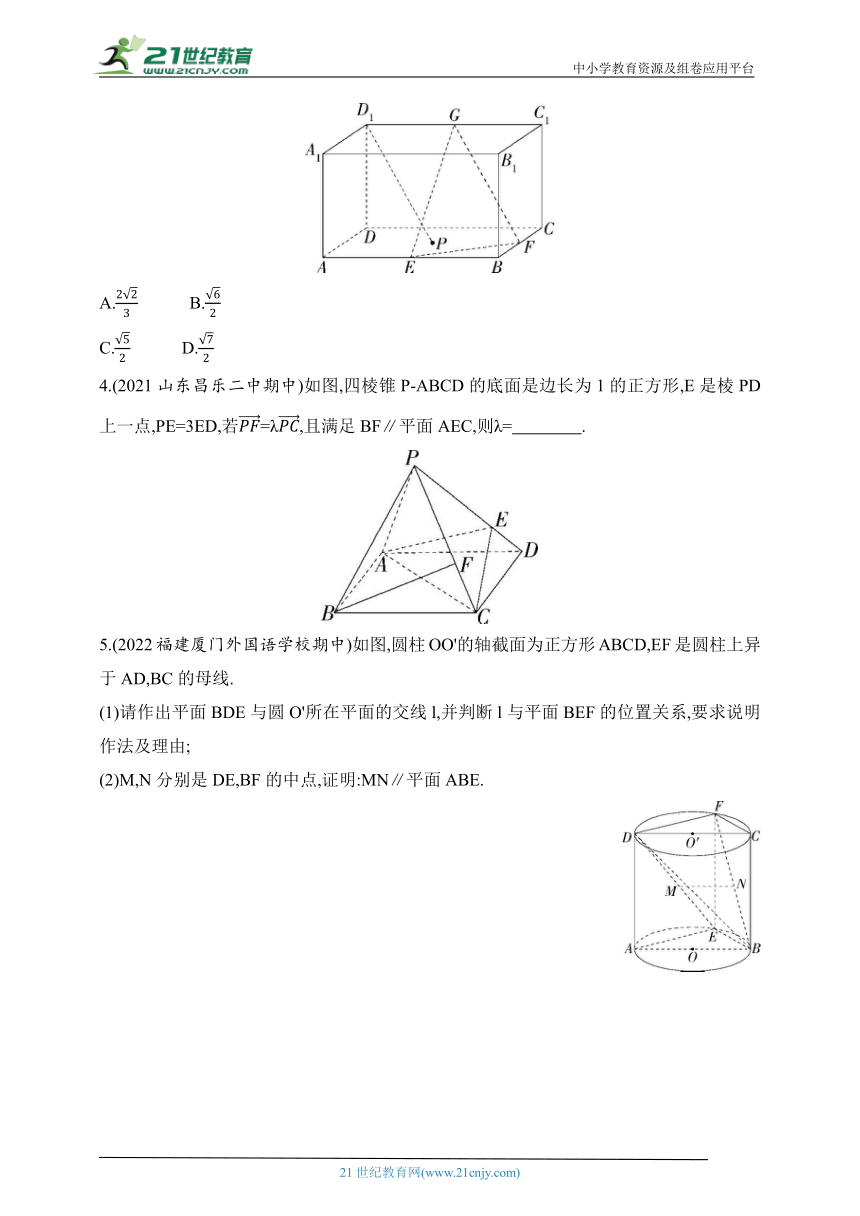
3.如图,在长方体ABCD-A1B1C1D1中,AD=DD1=1,AB=,E,F,G分别为AB,BC,C1D1的中点,点P在平面ABCD内,若直线D1P∥平面EFG,则点D1与点P的轨迹确定的平面截长方体所得截面的面积为( )
A. B.
C. D.
4.(2021山东昌乐二中期中)如图,四棱锥P-ABCD的底面是边长为1的正方形,E是棱PD上一点,PE=3ED,若=λ,且满足BF∥平面AEC,则λ= .
5.(2022福建厦门外国语学校期中)如图,圆柱OO'的轴截面为正方形ABCD,EF是圆柱上异于AD,BC的母线.
(1)请作出平面BDE与圆O'所在平面的交线l,并判断l与平面BEF的位置关系,要求说明作法及理由;
(2)M,N分别是DE,BF的中点,证明:MN∥平面ABE.
答案与分层梯度式解析
专题强化练8 空间中的平行关系
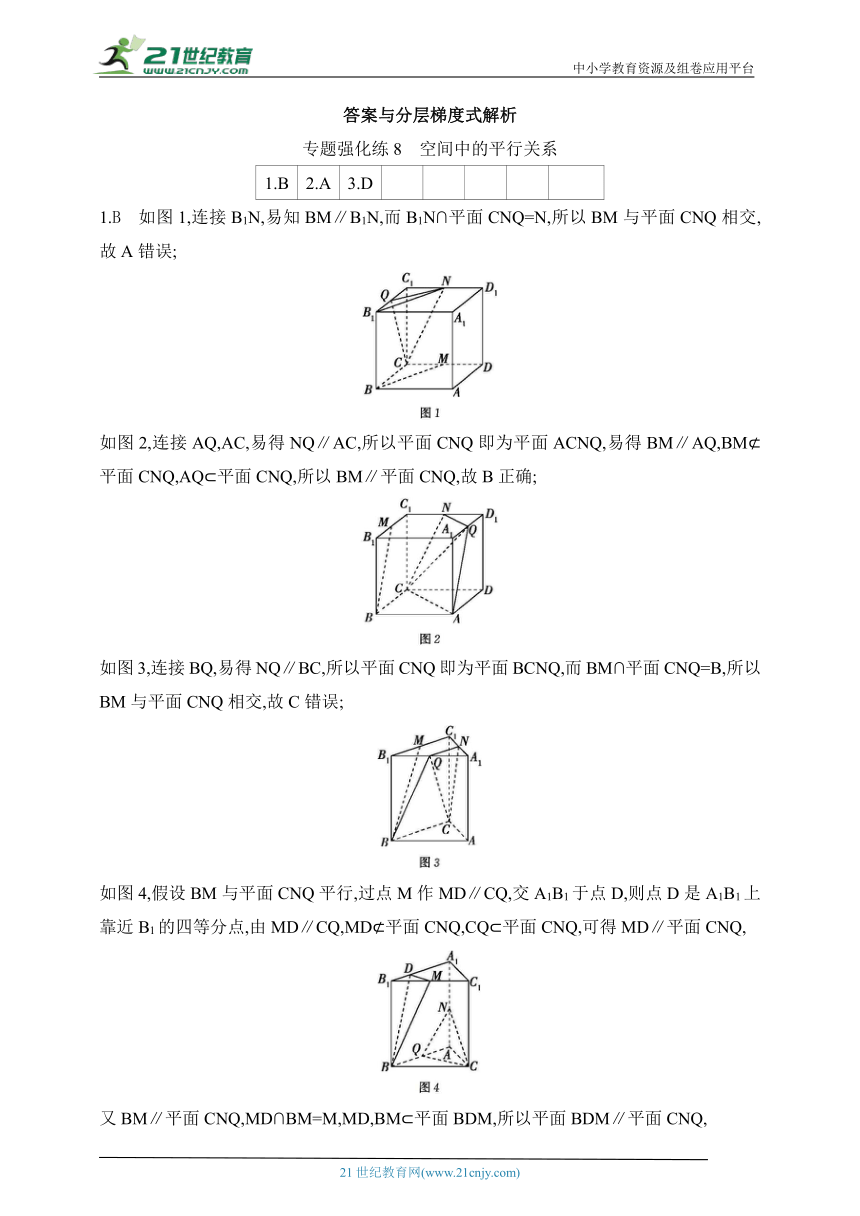
1.B 2.A 3.D
1.B 如图1,连接B1N,易知BM∥B1N,而B1N∩平面CNQ=N,所以BM与平面CNQ相交,故A错误;
如图2,连接AQ,AC,易得NQ∥AC,所以平面CNQ即为平面ACNQ,易得BM∥AQ,BM 平面CNQ,AQ 平面CNQ,所以BM∥平面CNQ,故B正确;
如图3,连接BQ,易得NQ∥BC,所以平面CNQ即为平面BCNQ,而BM∩平面CNQ=B,所以BM与平面CNQ相交,故C错误;
如图4,假设BM与平面CNQ平行,过点M作MD∥CQ,交A1B1于点D,则点D是A1B1上靠近B1的四等分点,由MD∥CQ,MD 平面CNQ,CQ 平面CNQ,可得MD∥平面CNQ,
又BM∥平面CNQ,MD∩BM=M,MD,BM 平面BDM,所以平面BDM∥平面CNQ,
而平面BDM∩平面ABB1A1=BD,平面CNQ∩平面ABB1A1=QN,则BD∥QN,
显然BD与QN不平行,故假设错误,所以BM与平面CNQ不平行,故D错误.
2.A 如图所示,连接A1B,D1C,BD,BD1,
由=2,可得EF∥A1B,且;同理可得GH∥CD1,且.
假设BD1∥GH,则由平行线的传递性,得BD1∥CD1,显然不成立,故A中说法错误;
易知BD与EF不平行,且不相交,由异面直线的定义可知,BD与EF异面,故B中说法正确;
在长方体ABCD-A1B1C1D1中,A1B∥CD1,A1B=CD1,
所以EF∥GH,EF=GH,即四边形EFGH为平行四边形,所以EH∥FG,
又BC∥FG,所以EH∥BC,因为EH 平面ABCD,BC 平面ABCD,所以EH∥平面ABCD,故C中说法正确;
由EF∥A1B,EF 平面A1BCD1,A1B 平面A1BCD1,得EF∥平面A1BCD1,
由BC∥FG,FG 平面A1BCD1,BC 平面A1BCD1,得FG∥平面A1BCD1,
又EF∩FG=F,且EF,FG 平面EFGH,
所以平面EFGH∥平面A1BCD1,故D中说法正确.
故选A.
3.D 如图,连接D1A,AC,D1C.
因为E,F分别为AB,BC的中点,
所以AC∥EF.
因为EF 平面ACD1,AC 平面ACD1,
所以EF∥平面ACD1.
因为E,G分别为AB,C1D1的中点,所以AED1G,
所以四边形AEGD1为平行四边形,所以EG∥AD1.
因为EG 平面ACD1,AD1 平面ACD1,
所以EG∥平面ACD1.
又EF∩EG=E,所以平面ACD1∥平面EFG,
所以点P在线段AC上,
则点D1与点P的轨迹确定的平面截长方体所得的截面为△ACD1及其内部,
在△ACD1中,AD1=,AC=2,CD1=2,
所以.
4.答案
解析 如图,连接BD,交AC于点O,连接OE,则BO=OD,
在线段PE上取一点G,使得GE=ED,
因为PE=3ED,所以PE=3GE,所以,
连接BG,FG,则BG∥OE,
又因为OE 平面AEC,BG 平面AEC,
所以BG∥平面AEC.
因为BF∥平面AEC,BG∩BF=B,BG,BF 平面BGF,
所以平面BGF∥平面AEC.
因为平面PCD∩平面BGF=GF,平面PCD∩平面AEC=EC,所以GF∥EC,
所以,故λ=.
5.解析 (1)交线l如图所示.
作法:在平面BDE中过D点作直线l∥BE,则直线l就是所求作的交线.
理由:在圆柱OO'中,EF,BC是母线,∴EF∥BC,EF=BC,
∴四边形EFCB是平行四边形,∴EB∥FC,
又∵EB 平面FCD,CF 平面FCD,
∴EB∥平面FCD.
∵交线l=平面FCD∩平面DBE,∴l∥EB,
∴过D作直线l∥EB,则直线l就是所求作的交线.
∵l∥EB,l 平面BEF,EB 平面BEF,
∴l∥平面BEF.
(2)证明:如图,取EF的中点G,连接MG,NG,
∵M,G分别是DE,EF的中点,∴MG∥DF,
∵MG 平面DFC,DF 平面DFC,
∴MG∥平面DFC,∴MG∥平面ABE,
同理可证GN∥平面ABE,
∵MG∩GN=G,MG,GN 平面MGN,
∴平面MGN∥平面ABE,
又∵MN 平面MGN,∴MN∥平面ABE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版高中数学必修第二册同步练习题
专题强化练8 空间中的平行关系
1.(2023河南新乡模拟)如图所示,在正方体或正三棱柱中,M,N,Q分别是所在棱的中点,则满足直线BM与平面CNQ平行的是( )
A B
C D
2.(2023新疆乌鲁木齐模拟)如图,在长方体ABCD-A1B1C1D1中,=2,则下列说法错误的是( )
A.BD1∥GH
B.BD与EF异面
C.EH∥平面ABCD
D.平面EFGH∥平面A1BCD1
3.如图,在长方体ABCD-A1B1C1D1中,AD=DD1=1,AB=,E,F,G分别为AB,BC,C1D1的中点,点P在平面ABCD内,若直线D1P∥平面EFG,则点D1与点P的轨迹确定的平面截长方体所得截面的面积为( )
A. B.
C. D.
4.(2021山东昌乐二中期中)如图,四棱锥P-ABCD的底面是边长为1的正方形,E是棱PD上一点,PE=3ED,若=λ,且满足BF∥平面AEC,则λ= .
5.(2022福建厦门外国语学校期中)如图,圆柱OO'的轴截面为正方形ABCD,EF是圆柱上异于AD,BC的母线.
(1)请作出平面BDE与圆O'所在平面的交线l,并判断l与平面BEF的位置关系,要求说明作法及理由;
(2)M,N分别是DE,BF的中点,证明:MN∥平面ABE.
答案与分层梯度式解析
专题强化练8 空间中的平行关系
1.B 2.A 3.D
1.B 如图1,连接B1N,易知BM∥B1N,而B1N∩平面CNQ=N,所以BM与平面CNQ相交,故A错误;
如图2,连接AQ,AC,易得NQ∥AC,所以平面CNQ即为平面ACNQ,易得BM∥AQ,BM 平面CNQ,AQ 平面CNQ,所以BM∥平面CNQ,故B正确;
如图3,连接BQ,易得NQ∥BC,所以平面CNQ即为平面BCNQ,而BM∩平面CNQ=B,所以BM与平面CNQ相交,故C错误;
如图4,假设BM与平面CNQ平行,过点M作MD∥CQ,交A1B1于点D,则点D是A1B1上靠近B1的四等分点,由MD∥CQ,MD 平面CNQ,CQ 平面CNQ,可得MD∥平面CNQ,
又BM∥平面CNQ,MD∩BM=M,MD,BM 平面BDM,所以平面BDM∥平面CNQ,
而平面BDM∩平面ABB1A1=BD,平面CNQ∩平面ABB1A1=QN,则BD∥QN,
显然BD与QN不平行,故假设错误,所以BM与平面CNQ不平行,故D错误.
2.A 如图所示,连接A1B,D1C,BD,BD1,
由=2,可得EF∥A1B,且;同理可得GH∥CD1,且.
假设BD1∥GH,则由平行线的传递性,得BD1∥CD1,显然不成立,故A中说法错误;
易知BD与EF不平行,且不相交,由异面直线的定义可知,BD与EF异面,故B中说法正确;
在长方体ABCD-A1B1C1D1中,A1B∥CD1,A1B=CD1,
所以EF∥GH,EF=GH,即四边形EFGH为平行四边形,所以EH∥FG,
又BC∥FG,所以EH∥BC,因为EH 平面ABCD,BC 平面ABCD,所以EH∥平面ABCD,故C中说法正确;
由EF∥A1B,EF 平面A1BCD1,A1B 平面A1BCD1,得EF∥平面A1BCD1,
由BC∥FG,FG 平面A1BCD1,BC 平面A1BCD1,得FG∥平面A1BCD1,
又EF∩FG=F,且EF,FG 平面EFGH,
所以平面EFGH∥平面A1BCD1,故D中说法正确.
故选A.
3.D 如图,连接D1A,AC,D1C.
因为E,F分别为AB,BC的中点,
所以AC∥EF.
因为EF 平面ACD1,AC 平面ACD1,
所以EF∥平面ACD1.
因为E,G分别为AB,C1D1的中点,所以AED1G,
所以四边形AEGD1为平行四边形,所以EG∥AD1.
因为EG 平面ACD1,AD1 平面ACD1,
所以EG∥平面ACD1.
又EF∩EG=E,所以平面ACD1∥平面EFG,
所以点P在线段AC上,
则点D1与点P的轨迹确定的平面截长方体所得的截面为△ACD1及其内部,
在△ACD1中,AD1=,AC=2,CD1=2,
所以.
4.答案
解析 如图,连接BD,交AC于点O,连接OE,则BO=OD,
在线段PE上取一点G,使得GE=ED,
因为PE=3ED,所以PE=3GE,所以,
连接BG,FG,则BG∥OE,
又因为OE 平面AEC,BG 平面AEC,
所以BG∥平面AEC.
因为BF∥平面AEC,BG∩BF=B,BG,BF 平面BGF,
所以平面BGF∥平面AEC.
因为平面PCD∩平面BGF=GF,平面PCD∩平面AEC=EC,所以GF∥EC,
所以,故λ=.
5.解析 (1)交线l如图所示.
作法:在平面BDE中过D点作直线l∥BE,则直线l就是所求作的交线.
理由:在圆柱OO'中,EF,BC是母线,∴EF∥BC,EF=BC,
∴四边形EFCB是平行四边形,∴EB∥FC,
又∵EB 平面FCD,CF 平面FCD,
∴EB∥平面FCD.
∵交线l=平面FCD∩平面DBE,∴l∥EB,
∴过D作直线l∥EB,则直线l就是所求作的交线.
∵l∥EB,l 平面BEF,EB 平面BEF,
∴l∥平面BEF.
(2)证明:如图,取EF的中点G,连接MG,NG,
∵M,G分别是DE,EF的中点,∴MG∥DF,
∵MG 平面DFC,DF 平面DFC,
∴MG∥平面DFC,∴MG∥平面ABE,
同理可证GN∥平面ABE,
∵MG∩GN=G,MG,GN 平面MGN,
∴平面MGN∥平面ABE,
又∵MN 平面MGN,∴MN∥平面ABE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
