2024北师版高中数学必修第二册同步练习题--专题强化练11 数学文化背景下的空间几何体问题(含解析)
文档属性
| 名称 | 2024北师版高中数学必修第二册同步练习题--专题强化练11 数学文化背景下的空间几何体问题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师版高中数学必修第二册同步练习题
专题强化练11 数学文化背景下的空间几何体问题
1.(多选题)(2023江苏连云港调研)折扇在我国已有三四千年的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它以字画的形式集中体现了我国文化的方方面面,是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若侧面展开图的两个圆弧所在圆的半径分别是1和3,且∠ABC=120°,则该圆台的( )
A.高为
B.表面积为π
C.体积为π
D.上底面面积、下底面面积和侧面积之比为1∶9∶24
2.(2021江苏无锡月考)斗拱是中国古典建筑最具装饰性的构件之一,并为中国所特有,图一、图二是北京故宫太和殿斗拱实物图,图三是斗拱构件之一的斗的几何示意图,图中的斗由棱台与长方体形凹槽(长方体去掉一个长相等,宽和高分别为原长方体一半的小长方体)组成.若棱台两底面面积分别是400 cm2,900 cm2,高为9 cm,长方体形凹槽的高为12 cm,斗的密度是0.50 g/cm3,那么这个斗的质量是( )
A.3 990 g B.3 010 g
C.6 900 g D.6 300 g
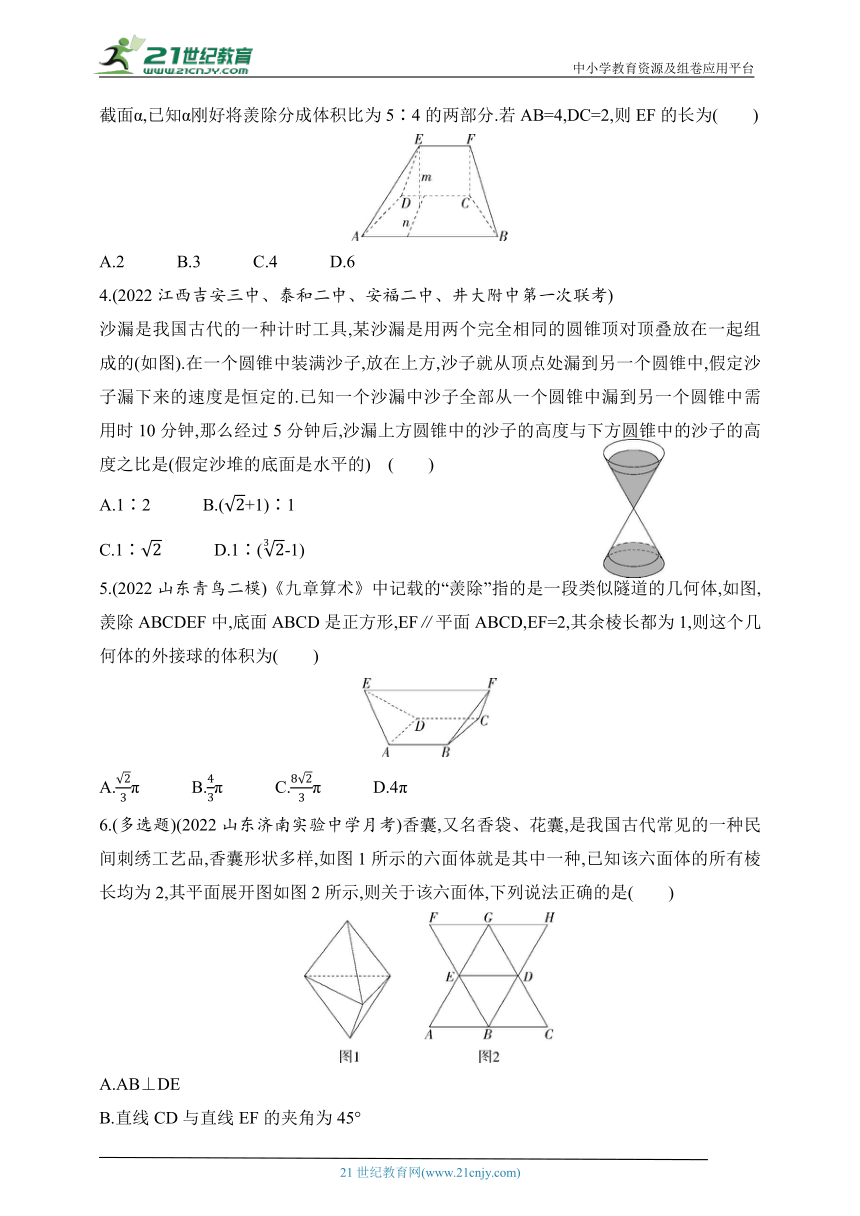
3.(2023上海四校联考)《九章算术》中所述“羡除”,是指下图所示的五面体ABCDEF,其中AB∥DC∥EF,“羡除”形似“楔体”.“广”是指“羡除”的三条平行侧棱之长a,b,c,“深”是指一条侧棱到另两条侧棱所在平面的距离m,“袤”是指这两条侧棱所在平行直线之间的距离n(如图).羡除的体积公式为V=,过线段AD,BC的中点G,H及直线EF作该羡除的一个截面α,已知α刚好将羡除分成体积比为5∶4的两部分.若AB=4,DC=2,则EF的长为( )
A.2 B.3 C.4 D.6
4.(2022江西吉安三中、泰和二中、安福二中、井大附中第一次联考)
沙漏是我国古代的一种计时工具,某沙漏是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟,那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的) ( )
A.1∶2 B.(+1)∶1
C.1∶ D.1∶(-1)
5.(2022山东青鸟二模)《九章算术》中记载的“羡除”指的是一段类似隧道的几何体,如图,羡除ABCDEF中,底面ABCD是正方形,EF∥平面ABCD,EF=2,其余棱长都为1,则这个几何体的外接球的体积为( )
A.π B.π C.π D.4π
6.(多选题)(2022山东济南实验中学月考)香囊,又名香袋、花囊,是我国古代常见的一种民间刺绣工艺品,香囊形状多样,如图1所示的六面体就是其中一种,已知该六面体的所有棱长均为2,其平面展开图如图2所示,则关于该六面体,下列说法正确的是( )
A.AB⊥DE
B.直线CD与直线EF的夹角为45°
C.该六面体的体积为
D.该六面体内切球的表面积是
7.有一传统智力玩具鲁班锁如图所示,它起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分即为榫卯结构啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六个完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁,其中每个正四棱柱的底面边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱的高为 .
8.(2022湖北华中师大一附中期中)《九章算术》中,底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马,四个面都为直角三角形的四面体称为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,E是PC的中点,连接DE,BD,BE.
(1)证明DE⊥平面PBC,并判断四面体E-BCD是不是鳖臑,若是,写出其每个面的直角,若不是,请说明理由;
(2)记阳马P-ABCD的体积为V1,四面体E-BCD的体积为V2,求.
答案与分层梯度式解析
专题强化练11 数学文化背景下的空间几何体问题
1.BCD 2.C 3.B 4.D 5.B 6.AD
1.BCD 对于A,设圆台的上底面半径为r,下底面半径为R,则2πr=×2π×3,解得r=,R=1,又圆台的母线长为3-1=2,所以圆台的高h=,故A错误;
对于B,圆台的上底面面积为π,下底面面积为π,侧面积为π×π,
所以圆台的表面积S=π,故B正确;
对于C,圆台的体积V=,故C正确;
对于D,圆台的上底面面积、下底面面积和侧面积之比为π=1∶9∶24,故D正确.
故选BCD.
2.C 信息提取 ①斗由棱台与长方体形凹槽组成;②长方体形凹槽的中空部分与原长方体的长相等,宽和高分别为原长方体的一半;③斗的密度是0.50 g/cm3.
数学建模 本题以中国所特有的古典建筑最具装饰性的构件之一斗拱为背景,以考查几何体斗的质量为载体,考查几何体斗的体积的运算,同时也跨学科考查了质量、密度与体积之间的关系.可以设长方体的长为x cm,宽为y cm,则长方体底面面积为xy=900 cm2,由长方体形凹槽的高为12 cm,可以求出长方体形凹槽的体积,进而得出几何体斗的体积,从而使问题得到解决.
解析 由题意可知,棱台的体积V台=)×9=5 700(cm3),
设长方体的长为x cm,宽为y cm,则xy=900,因为长方体形凹槽的高为12 cm,
所以长方体形凹槽的体积V=12xy-6x·y=9xy=8 100(cm3),
所以斗的体积为5 700+8 100=13 800(cm3),
因此斗的质量为13 800×0.5=6 900(g).故选C.
3.B 因为AB=4,DC=2,AB∥DC∥EF,G,H为线段AD,BC的中点,
所以GH∥AB∥CD,GH=(AB+CD)=3,
所以V五面体GHCDEF=,V五面体ABHGEF=,
因为,即,所以EF=3.
4.D 5分钟刚好是总用时的一半,而沙子漏下来的速度是恒定的,所以漏下来的沙子是全部沙子的一半,下方圆锥的空白部分就是上方圆锥中的沙子占的部分,所以可以单独研究下方圆锥.下方圆锥被沙子的上底面分成体积相等的两部分,所以,所以,所以 .故选D.
5.B 连接AC,BD交于点M,取EF的中点O,连接OA,OM,易得OM⊥平面ABCD,取BC的中点G,连接FG,过点G作GH⊥EF于点H,
由题意可得HF=,则HG=,
易得OM=HG=,则OA==1,
由对称的性质得OB=OC=OD=OA=1,
又OE=OF=1,所以这个几何体的外接球的球心为O,半径为1,
所以这个几何体的外接球的体积为π,故选B.
6.AD 由题知所给六面体由两个同底面的正四面体组成,将题图2的平面展开图还原为六面体后如图所示,其中A,C,F,H四点重合.
对于A,取DE的中点M,连接AM,BM,则AM⊥DE,BM⊥DE.∵AM∩BM=M,∴DE⊥平面ABM.又AB 平面ABM,∴AB⊥DE,故A中说法正确.
对于B,由图可知,CD与EF分别为正三角形ADE的边AD,AE,其夹角为60°,故B中说法错误.
对于C,连接GM,过点G作GO⊥平面ADE,垂足为O,则O在AM上且为正三角形ADE的中心,又AM=GM=,∴该六面体的体积V=2V四面体G-ADE=2×,故C中说法错误.
对于D,∵该六面体的各棱长均相等,∴其内切球的球心必在面ADE上,又∵△ADE为正三角形,∴点O即为该六面体内切球的球心,且该球与GM相切,过点O作ON⊥GM于点N,则ON就是此内切球的半径.在Rt△GOM中,GO·OM=GM·ON,∴ON=,∴该内切球的表面积为4π×,故D中说法正确.故选AD.
7.答案 5
解析 由题意知球形容器外接于一个长、宽、高分别为2,1,h的长方体,其中h为正四棱柱的高,该长方体的外接球半径R=,据此可得S=4πR2=(22+12+h2)π=30π,所以h=5,即正四棱柱的高为5.
8.解析 (1)因为PD⊥底面ABCD,BC 平面ABCD,所以PD⊥BC,由底面ABCD为矩形,得BC⊥CD,而PD∩CD=D,所以BC⊥平面PCD,又DE 平面PCD,所以BC⊥DE.因为PD=CD,E是PC的中点,所以DE⊥PC,而PC∩BC=C,所以DE⊥平面PBC.
由BC⊥平面PCD,DE⊥平面PBC可知四面体E-BCD的四个面都是直角三角形,即四面体E-BCD是鳖臑,其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB.
(2)由已知得,PD是阳马P-ABCD的高,所以V1=S四边形ABCD·PD=BC·CD·PD.
由(1)知,DE是鳖臑E-BCD的高,BC⊥CE,
所以V2=S△BCE·DE=BC·CE·DE.
在Rt△PDC中,因为PD=CD,E是PC的中点,所以DE=CE=CD,
于是=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版高中数学必修第二册同步练习题
专题强化练11 数学文化背景下的空间几何体问题
1.(多选题)(2023江苏连云港调研)折扇在我国已有三四千年的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它以字画的形式集中体现了我国文化的方方面面,是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若侧面展开图的两个圆弧所在圆的半径分别是1和3,且∠ABC=120°,则该圆台的( )
A.高为
B.表面积为π
C.体积为π
D.上底面面积、下底面面积和侧面积之比为1∶9∶24
2.(2021江苏无锡月考)斗拱是中国古典建筑最具装饰性的构件之一,并为中国所特有,图一、图二是北京故宫太和殿斗拱实物图,图三是斗拱构件之一的斗的几何示意图,图中的斗由棱台与长方体形凹槽(长方体去掉一个长相等,宽和高分别为原长方体一半的小长方体)组成.若棱台两底面面积分别是400 cm2,900 cm2,高为9 cm,长方体形凹槽的高为12 cm,斗的密度是0.50 g/cm3,那么这个斗的质量是( )
A.3 990 g B.3 010 g
C.6 900 g D.6 300 g
3.(2023上海四校联考)《九章算术》中所述“羡除”,是指下图所示的五面体ABCDEF,其中AB∥DC∥EF,“羡除”形似“楔体”.“广”是指“羡除”的三条平行侧棱之长a,b,c,“深”是指一条侧棱到另两条侧棱所在平面的距离m,“袤”是指这两条侧棱所在平行直线之间的距离n(如图).羡除的体积公式为V=,过线段AD,BC的中点G,H及直线EF作该羡除的一个截面α,已知α刚好将羡除分成体积比为5∶4的两部分.若AB=4,DC=2,则EF的长为( )
A.2 B.3 C.4 D.6
4.(2022江西吉安三中、泰和二中、安福二中、井大附中第一次联考)
沙漏是我国古代的一种计时工具,某沙漏是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟,那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的) ( )
A.1∶2 B.(+1)∶1
C.1∶ D.1∶(-1)
5.(2022山东青鸟二模)《九章算术》中记载的“羡除”指的是一段类似隧道的几何体,如图,羡除ABCDEF中,底面ABCD是正方形,EF∥平面ABCD,EF=2,其余棱长都为1,则这个几何体的外接球的体积为( )
A.π B.π C.π D.4π
6.(多选题)(2022山东济南实验中学月考)香囊,又名香袋、花囊,是我国古代常见的一种民间刺绣工艺品,香囊形状多样,如图1所示的六面体就是其中一种,已知该六面体的所有棱长均为2,其平面展开图如图2所示,则关于该六面体,下列说法正确的是( )
A.AB⊥DE
B.直线CD与直线EF的夹角为45°
C.该六面体的体积为
D.该六面体内切球的表面积是
7.有一传统智力玩具鲁班锁如图所示,它起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分即为榫卯结构啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六个完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁,其中每个正四棱柱的底面边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱的高为 .
8.(2022湖北华中师大一附中期中)《九章算术》中,底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马,四个面都为直角三角形的四面体称为鳖臑.在如图所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,E是PC的中点,连接DE,BD,BE.
(1)证明DE⊥平面PBC,并判断四面体E-BCD是不是鳖臑,若是,写出其每个面的直角,若不是,请说明理由;
(2)记阳马P-ABCD的体积为V1,四面体E-BCD的体积为V2,求.
答案与分层梯度式解析
专题强化练11 数学文化背景下的空间几何体问题
1.BCD 2.C 3.B 4.D 5.B 6.AD
1.BCD 对于A,设圆台的上底面半径为r,下底面半径为R,则2πr=×2π×3,解得r=,R=1,又圆台的母线长为3-1=2,所以圆台的高h=,故A错误;
对于B,圆台的上底面面积为π,下底面面积为π,侧面积为π×π,
所以圆台的表面积S=π,故B正确;
对于C,圆台的体积V=,故C正确;
对于D,圆台的上底面面积、下底面面积和侧面积之比为π=1∶9∶24,故D正确.
故选BCD.
2.C 信息提取 ①斗由棱台与长方体形凹槽组成;②长方体形凹槽的中空部分与原长方体的长相等,宽和高分别为原长方体的一半;③斗的密度是0.50 g/cm3.
数学建模 本题以中国所特有的古典建筑最具装饰性的构件之一斗拱为背景,以考查几何体斗的质量为载体,考查几何体斗的体积的运算,同时也跨学科考查了质量、密度与体积之间的关系.可以设长方体的长为x cm,宽为y cm,则长方体底面面积为xy=900 cm2,由长方体形凹槽的高为12 cm,可以求出长方体形凹槽的体积,进而得出几何体斗的体积,从而使问题得到解决.
解析 由题意可知,棱台的体积V台=)×9=5 700(cm3),
设长方体的长为x cm,宽为y cm,则xy=900,因为长方体形凹槽的高为12 cm,
所以长方体形凹槽的体积V=12xy-6x·y=9xy=8 100(cm3),
所以斗的体积为5 700+8 100=13 800(cm3),
因此斗的质量为13 800×0.5=6 900(g).故选C.
3.B 因为AB=4,DC=2,AB∥DC∥EF,G,H为线段AD,BC的中点,
所以GH∥AB∥CD,GH=(AB+CD)=3,
所以V五面体GHCDEF=,V五面体ABHGEF=,
因为,即,所以EF=3.
4.D 5分钟刚好是总用时的一半,而沙子漏下来的速度是恒定的,所以漏下来的沙子是全部沙子的一半,下方圆锥的空白部分就是上方圆锥中的沙子占的部分,所以可以单独研究下方圆锥.下方圆锥被沙子的上底面分成体积相等的两部分,所以,所以,所以 .故选D.
5.B 连接AC,BD交于点M,取EF的中点O,连接OA,OM,易得OM⊥平面ABCD,取BC的中点G,连接FG,过点G作GH⊥EF于点H,
由题意可得HF=,则HG=,
易得OM=HG=,则OA==1,
由对称的性质得OB=OC=OD=OA=1,
又OE=OF=1,所以这个几何体的外接球的球心为O,半径为1,
所以这个几何体的外接球的体积为π,故选B.
6.AD 由题知所给六面体由两个同底面的正四面体组成,将题图2的平面展开图还原为六面体后如图所示,其中A,C,F,H四点重合.
对于A,取DE的中点M,连接AM,BM,则AM⊥DE,BM⊥DE.∵AM∩BM=M,∴DE⊥平面ABM.又AB 平面ABM,∴AB⊥DE,故A中说法正确.
对于B,由图可知,CD与EF分别为正三角形ADE的边AD,AE,其夹角为60°,故B中说法错误.
对于C,连接GM,过点G作GO⊥平面ADE,垂足为O,则O在AM上且为正三角形ADE的中心,又AM=GM=,∴该六面体的体积V=2V四面体G-ADE=2×,故C中说法错误.
对于D,∵该六面体的各棱长均相等,∴其内切球的球心必在面ADE上,又∵△ADE为正三角形,∴点O即为该六面体内切球的球心,且该球与GM相切,过点O作ON⊥GM于点N,则ON就是此内切球的半径.在Rt△GOM中,GO·OM=GM·ON,∴ON=,∴该内切球的表面积为4π×,故D中说法正确.故选AD.
7.答案 5
解析 由题意知球形容器外接于一个长、宽、高分别为2,1,h的长方体,其中h为正四棱柱的高,该长方体的外接球半径R=,据此可得S=4πR2=(22+12+h2)π=30π,所以h=5,即正四棱柱的高为5.
8.解析 (1)因为PD⊥底面ABCD,BC 平面ABCD,所以PD⊥BC,由底面ABCD为矩形,得BC⊥CD,而PD∩CD=D,所以BC⊥平面PCD,又DE 平面PCD,所以BC⊥DE.因为PD=CD,E是PC的中点,所以DE⊥PC,而PC∩BC=C,所以DE⊥平面PBC.
由BC⊥平面PCD,DE⊥平面PBC可知四面体E-BCD的四个面都是直角三角形,即四面体E-BCD是鳖臑,其四个面的直角分别是∠BCD,∠BCE,∠DEC,∠DEB.
(2)由已知得,PD是阳马P-ABCD的高,所以V1=S四边形ABCD·PD=BC·CD·PD.
由(1)知,DE是鳖臑E-BCD的高,BC⊥CE,
所以V2=S△BCE·DE=BC·CE·DE.
在Rt△PDC中,因为PD=CD,E是PC的中点,所以DE=CE=CD,
于是=4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
