2024北师版高中数学必修第二册同步练习题--1.1 构成空间几何体的基本元素 1.2 简单多面体——棱柱、棱锥和棱台(含解析)
文档属性
| 名称 | 2024北师版高中数学必修第二册同步练习题--1.1 构成空间几何体的基本元素 1.2 简单多面体——棱柱、棱锥和棱台(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师版高中数学必修第二册同步练习题
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
题组一 空间几何体的基本元素
1.下列不属于构成空间几何体的基本元素的是 ( )
A.点
B.线
C.曲面
D.多边形(不包括内部的点)
2.在第二十四届冬奥会上,中国代表队创造了历史最好成绩,首都北京也成为第一座“双奥之城”.如图所示,坐落于北京的国家游泳中心(又称“水立方”)是中国健儿为国争光的地方,“水立方”可以抽象出的几何体是( )
A.圆柱 B.四棱锥
C.四棱台 D.长方体
题组二 棱柱的结构特征
3.(多选题)(2022浙江宁波六校联盟期中)下列命题为假命题的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.四棱柱的侧棱必与底面垂直
C.有两个侧面是矩形的四棱柱是直四棱柱
D.正四棱柱是平行六面体
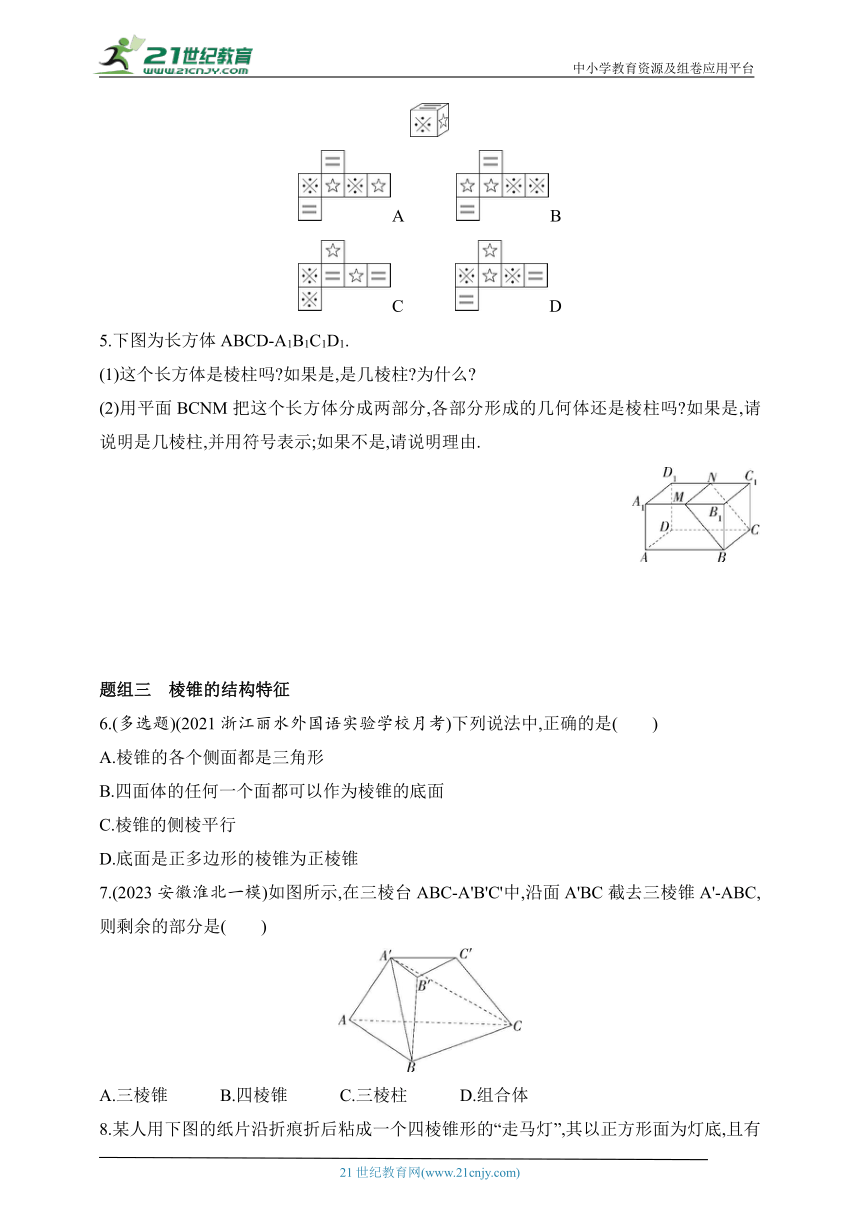
4.(2023四川眉山北外附属东坡外国语学校月考)某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A B
C D
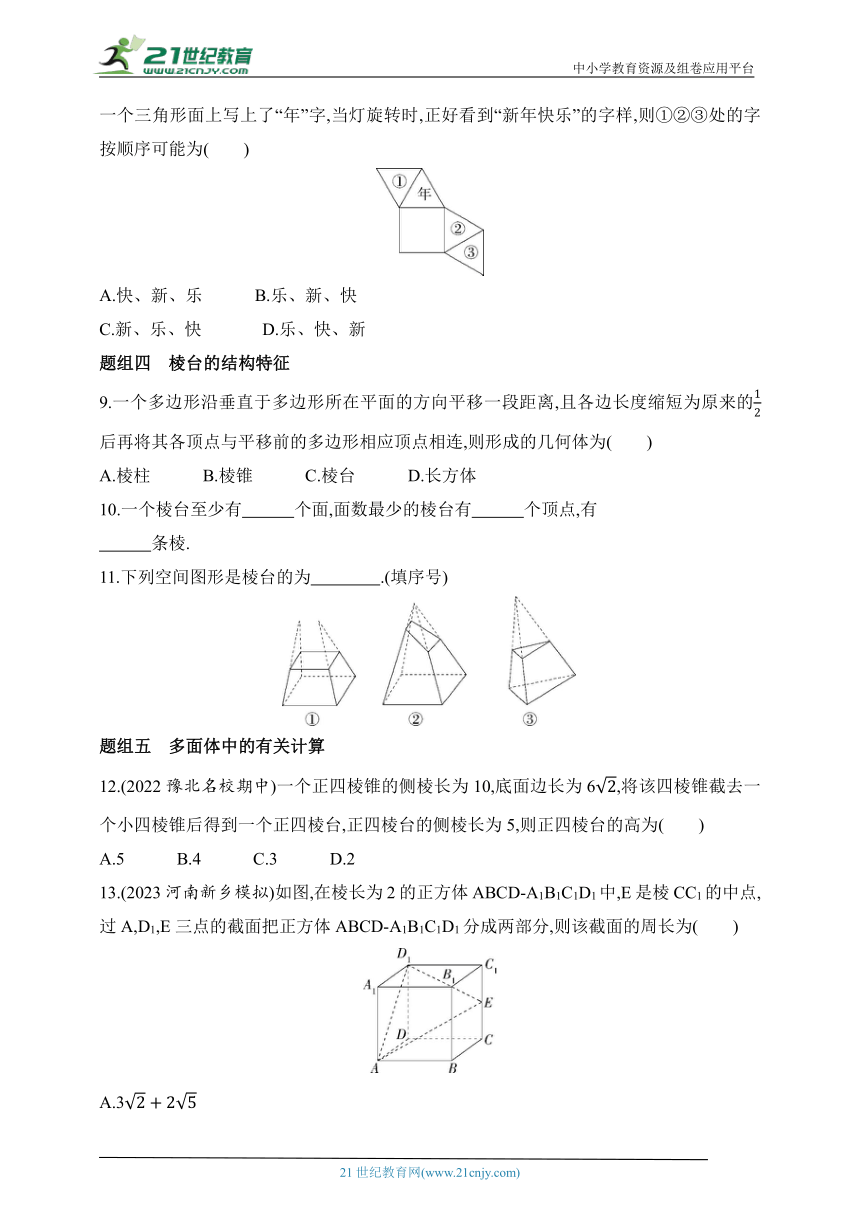
5.下图为长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗 如果是,是几棱柱 为什么
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗 如果是,请说明是几棱柱,并用符号表示;如果不是,请说明理由.
题组三 棱锥的结构特征
6.(多选题)(2021浙江丽水外国语实验学校月考)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱平行
D.底面是正多边形的棱锥为正棱锥
7.(2023安徽淮北一模)如图所示,在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
8.某人用下图的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,其以正方形面为灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则①②③处的字按顺序可能为( )
A.快、新、乐 B.乐、新、快
C.新、乐、快 D.乐、快、新
题组四 棱台的结构特征
9.一个多边形沿垂直于多边形所在平面的方向平移一段距离,且各边长度缩短为原来的后再将其各顶点与平移前的多边形相应顶点相连,则形成的几何体为( )
A.棱柱 B.棱锥 C.棱台 D.长方体
10.一个棱台至少有 个面,面数最少的棱台有 个顶点,有
条棱.
11.下列空间图形是棱台的为 .(填序号)
题组五 多面体中的有关计算
12.(2022豫北名校期中)一个正四棱锥的侧棱长为10,底面边长为6,将该四棱锥截去一个小四棱锥后得到一个正四棱台,正四棱台的侧棱长为5,则正四棱台的高为( )
A.5 B.4 C.3 D.2
13.(2023河南新乡模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,过A,D1,E三点的截面把正方体ABCD-A1B1C1D1分成两部分,则该截面的周长为( )
A.3
B.2+3
C.
D.2
14.一个直平行六面体的侧棱长是9,底面相邻的两边的长都是6,底面四边形的一个内角是60°,则此直平行六面体的体对角线长是 .
15.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .
16.正三棱台的高为3,上、下底面的边长分别为2和4,求这个棱台的侧棱长和斜高.
答案与分层梯度式解析
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
1.D 2.D 3.ABC 4.A 6.AB 7.B 8.A 9.C
12.B 13.A
1.D
2.D
3.ABC 对于A,当直四棱柱的底面不是矩形时,其不是长方体,故A是假命题;
对于B,只有直四棱柱的侧棱才与底面垂直,故B是假命题;
对于C,一组相对侧面是矩形的平行六面体不一定是直四棱柱,故C是假命题;
显然D是真命题.故选ABC.
4.A 沿该正方体礼品盒的棱剪开,无论从哪条棱剪开,剪开的相邻面在展开图中可以不相邻,但未剪开的相邻面在展开图中一定相邻,又正方体礼品盒各组对面的图案相同,所以展开后相同图案绝不会相邻.故选A.
5.解析 (1)是棱柱,并且是四棱柱,因为长方体有相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义,又因为底面是四边形,所以长方体是四棱柱.
(2)是.截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
6.AB 由棱锥的定义可知棱锥的各个侧面都是三角形,故A正确;
四面体是由四个三角形围成的封闭图形,所以四面体的任何一个面都可以作为棱锥的底面,故B正确;
棱锥的侧棱相交于一点,故C不正确;
若棱锥的顶点在底面上的射影不是正多边形的中心,则此棱锥不是正棱锥,故D不正确.故选AB.
7.B 在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC后,剩余的部分是四棱锥A'-BCC'B'.故选B.
8.A
9.C 一个多边形沿垂直于它所在平面的方向平移一段距离,各边长度缩短为原来的,平移前多边形和平移后多边形所在的平面平行,各边长度缩短后的多边形与原多边形相似,且相对应的顶点的连线所在直线能相交于一点,符合棱台的结构特征,故形成的几何体为棱台,故选C.
10.答案 5;6;9
解析 面数最少的棱台为三棱台,它有5个面,6个顶点,9条棱.
11.答案 ③
解析 由棱台的定义知,棱台的上底面必须与下底面平行,且侧棱的延长线能交于一点.
①中侧棱延长后不能交于一点,②中上底面不平行于下底面,故①和②都不是棱台.
③符合棱台的结构特征.
12.B 根据题意,正四棱台是由过原正四棱锥侧棱的中点且与底面平行的平面截得的,如图所示,PO为原正四棱锥的高,OO1为所得正四棱台的高,
原正四棱锥中,BD=BC=12,故其高PO==8,
又△PO1B1∽△POB,且其相似比为1∶2,故正四棱台的高OO1=PO=4.
13.A 如图,补全的截面为四边形AFED1,F为BC的中点,
因为正方体ABCD-A1B1C1D1的棱长为2,
所以EF=,
所以四边形AFED1的周长为3.
14.答案 3和3
解析 直平行六面体的体对角线有4条,共分长度分别相等的两对,底面菱形的对角线长分别是6和6,由勾股定理可得此直平行六面体的体对角线长分别是.
15.答案 a2
解析 不妨作截面SAC,取AC的中点O,连接SO,则SO⊥AC,如图所示.
∵正四棱锥 S-ABCD的所有棱长都等于a,
∴AC=a,
∴截面SAC的面积为a2.
16.解析 如图,在正三棱台ABC-A1B1C1中,两底面中心分别为O,O1,AB和A1B1的中点分别是E,E1,连接OO1,EE1,O1A1,OA,O1E1,OE,则四边形OAA1O1,四边形OEE1O1都是直角梯形.
在等边△ABC中,AB=4,则OA=.在等边△A1B1C1中,A1B1=2,则O1A1=.
在直角梯形OAA1O1中,OO1=3,
所以AA1=
=,
即棱台的侧棱长为.
在直角梯形OEE1O1中,EE1=
=,
即棱台的斜高为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版高中数学必修第二册同步练习题
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
题组一 空间几何体的基本元素
1.下列不属于构成空间几何体的基本元素的是 ( )
A.点
B.线
C.曲面
D.多边形(不包括内部的点)
2.在第二十四届冬奥会上,中国代表队创造了历史最好成绩,首都北京也成为第一座“双奥之城”.如图所示,坐落于北京的国家游泳中心(又称“水立方”)是中国健儿为国争光的地方,“水立方”可以抽象出的几何体是( )
A.圆柱 B.四棱锥
C.四棱台 D.长方体
题组二 棱柱的结构特征
3.(多选题)(2022浙江宁波六校联盟期中)下列命题为假命题的是( )
A.长方体是四棱柱,直四棱柱是长方体
B.四棱柱的侧棱必与底面垂直
C.有两个侧面是矩形的四棱柱是直四棱柱
D.正四棱柱是平行六面体
4.(2023四川眉山北外附属东坡外国语学校月考)某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A B
C D
5.下图为长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗 如果是,是几棱柱 为什么
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗 如果是,请说明是几棱柱,并用符号表示;如果不是,请说明理由.
题组三 棱锥的结构特征
6.(多选题)(2021浙江丽水外国语实验学校月考)下列说法中,正确的是( )
A.棱锥的各个侧面都是三角形
B.四面体的任何一个面都可以作为棱锥的底面
C.棱锥的侧棱平行
D.底面是正多边形的棱锥为正棱锥
7.(2023安徽淮北一模)如图所示,在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.组合体
8.某人用下图的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,其以正方形面为灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则①②③处的字按顺序可能为( )
A.快、新、乐 B.乐、新、快
C.新、乐、快 D.乐、快、新
题组四 棱台的结构特征
9.一个多边形沿垂直于多边形所在平面的方向平移一段距离,且各边长度缩短为原来的后再将其各顶点与平移前的多边形相应顶点相连,则形成的几何体为( )
A.棱柱 B.棱锥 C.棱台 D.长方体
10.一个棱台至少有 个面,面数最少的棱台有 个顶点,有
条棱.
11.下列空间图形是棱台的为 .(填序号)
题组五 多面体中的有关计算
12.(2022豫北名校期中)一个正四棱锥的侧棱长为10,底面边长为6,将该四棱锥截去一个小四棱锥后得到一个正四棱台,正四棱台的侧棱长为5,则正四棱台的高为( )
A.5 B.4 C.3 D.2
13.(2023河南新乡模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,过A,D1,E三点的截面把正方体ABCD-A1B1C1D1分成两部分,则该截面的周长为( )
A.3
B.2+3
C.
D.2
14.一个直平行六面体的侧棱长是9,底面相邻的两边的长都是6,底面四边形的一个内角是60°,则此直平行六面体的体对角线长是 .
15.正四棱锥S-ABCD的所有棱长都等于a,过不相邻的两条侧棱作截面,则截面的面积为 .
16.正三棱台的高为3,上、下底面的边长分别为2和4,求这个棱台的侧棱长和斜高.
答案与分层梯度式解析
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
1.D 2.D 3.ABC 4.A 6.AB 7.B 8.A 9.C
12.B 13.A
1.D
2.D
3.ABC 对于A,当直四棱柱的底面不是矩形时,其不是长方体,故A是假命题;
对于B,只有直四棱柱的侧棱才与底面垂直,故B是假命题;
对于C,一组相对侧面是矩形的平行六面体不一定是直四棱柱,故C是假命题;
显然D是真命题.故选ABC.
4.A 沿该正方体礼品盒的棱剪开,无论从哪条棱剪开,剪开的相邻面在展开图中可以不相邻,但未剪开的相邻面在展开图中一定相邻,又正方体礼品盒各组对面的图案相同,所以展开后相同图案绝不会相邻.故选A.
5.解析 (1)是棱柱,并且是四棱柱,因为长方体有相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义,又因为底面是四边形,所以长方体是四棱柱.
(2)是.截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
6.AB 由棱锥的定义可知棱锥的各个侧面都是三角形,故A正确;
四面体是由四个三角形围成的封闭图形,所以四面体的任何一个面都可以作为棱锥的底面,故B正确;
棱锥的侧棱相交于一点,故C不正确;
若棱锥的顶点在底面上的射影不是正多边形的中心,则此棱锥不是正棱锥,故D不正确.故选AB.
7.B 在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC后,剩余的部分是四棱锥A'-BCC'B'.故选B.
8.A
9.C 一个多边形沿垂直于它所在平面的方向平移一段距离,各边长度缩短为原来的,平移前多边形和平移后多边形所在的平面平行,各边长度缩短后的多边形与原多边形相似,且相对应的顶点的连线所在直线能相交于一点,符合棱台的结构特征,故形成的几何体为棱台,故选C.
10.答案 5;6;9
解析 面数最少的棱台为三棱台,它有5个面,6个顶点,9条棱.
11.答案 ③
解析 由棱台的定义知,棱台的上底面必须与下底面平行,且侧棱的延长线能交于一点.
①中侧棱延长后不能交于一点,②中上底面不平行于下底面,故①和②都不是棱台.
③符合棱台的结构特征.
12.B 根据题意,正四棱台是由过原正四棱锥侧棱的中点且与底面平行的平面截得的,如图所示,PO为原正四棱锥的高,OO1为所得正四棱台的高,
原正四棱锥中,BD=BC=12,故其高PO==8,
又△PO1B1∽△POB,且其相似比为1∶2,故正四棱台的高OO1=PO=4.
13.A 如图,补全的截面为四边形AFED1,F为BC的中点,
因为正方体ABCD-A1B1C1D1的棱长为2,
所以EF=,
所以四边形AFED1的周长为3.
14.答案 3和3
解析 直平行六面体的体对角线有4条,共分长度分别相等的两对,底面菱形的对角线长分别是6和6,由勾股定理可得此直平行六面体的体对角线长分别是.
15.答案 a2
解析 不妨作截面SAC,取AC的中点O,连接SO,则SO⊥AC,如图所示.
∵正四棱锥 S-ABCD的所有棱长都等于a,
∴AC=a,
∴截面SAC的面积为a2.
16.解析 如图,在正三棱台ABC-A1B1C1中,两底面中心分别为O,O1,AB和A1B1的中点分别是E,E1,连接OO1,EE1,O1A1,OA,O1E1,OE,则四边形OAA1O1,四边形OEE1O1都是直角梯形.
在等边△ABC中,AB=4,则OA=.在等边△A1B1C1中,A1B1=2,则O1A1=.
在直角梯形OAA1O1中,OO1=3,
所以AA1=
=,
即棱台的侧棱长为.
在直角梯形OEE1O1中,EE1=
=,
即棱台的斜高为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
