2024北师版高中数学必修第二册同步练习题--6.1 柱、锥、台的侧面展开与面积(含解析)
文档属性
| 名称 | 2024北师版高中数学必修第二册同步练习题--6.1 柱、锥、台的侧面展开与面积(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:25:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师版高中数学必修第二册同步练习题
第六章 立体几何初步
§6 简单几何体的再认识
6.1 柱、锥、台的侧面展开与面积
基础过关练
题组一 圆柱、圆锥、圆台的表(侧)面积
1.(2022河南焦作二模)已知圆柱的轴截面是面积为100的正方形,则该圆柱的侧面积为( )
A.50π B.200
C.100π D.150π
2.(2023云南昆明三中适应性考试)用一个平行于圆锥底面的平面去截圆锥,截得的圆台的上底面半径为1,下底面半径为2,且该圆台的侧面积为3π,则原圆锥的母线长为( )
A.2 B. C.4 D.2
3.(2023河北邯郸鸡泽第一中学月考)已知某等腰直角三角形的直角边长为1,现将该三角形绕其某一边所在直线旋转一周,则所形成的几何体的表面积为( )
A.π B.π或(1+)π
C.2π D.2π或(2+)π
4.(2023湖南邵阳邵东四中期中)若圆锥的侧面积与过轴的截面面积的比值为2π,则其母线与轴的夹角的大小为 .
5.(2023上海四校联考)已知圆锥的底面半径为2,底面圆心到某条母线的距离为1,则该圆锥的侧面积为 .
6.以圆柱的上底中心为顶点,下底面为底面作圆锥,假设圆柱的侧面积为6,圆锥的侧面积为5,求圆柱的底面半径.
题组二 棱柱、棱锥、棱台的表(侧)面积
7.已知某长方体同一顶点上的三条棱的长分别为1,2,3,则该长方体的表面积为( )
A.22 B.20 C.10 D.11
8.(2022重庆十一中月考)正四棱台的上底面边长a=2 cm,下底面边长b=4 cm,侧棱长l=2 cm,则棱台的侧面积为( )
A.6 cm2 B.24 cm2
C.3 cm2 D.12 cm2
9.(2022重庆渝东六校共同体期中)已知一个直四棱柱的高为2,其底面水平放置的直观图(用斜二测画法画出)是边长为1的正方形,则这个直四棱柱的表面积为( )
A.10 B.8+4
C.16+4 D.16+4
10.若正三棱锥P-ABC的高为1,AB=4,则该正三棱锥的侧面积为( )
A.6 B.18 C.6 D.6
11.(2023浙江北斗联盟期中)由华裔建筑师贝聿铭设计的巴黎卢浮宫玻璃金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),其侧面三角形底边上的高与底面正方形边长的比值为,则以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为( )
A.2 B.
C. D.4
12.(2023北京第一六六中学期中)若四面体各棱的长是1或2,且该四面体不是正四面体,则其表面积可能是 .(只需写出一个可能的值)
13.正六棱柱的一条最长的体对角线长是13,侧面积为180,求此正六棱柱的表面积.
14.(2022重庆巫山官渡中学月考)如图,在三棱锥P-ABC中,E,F分别是AB,AP的中点.
(1)求证:EF∥平面PBC;
(2)若三棱锥P-ABC的各棱长均为2,求它的表面积.
题组三 组合体的表(侧)面积
15.(2023甘肃兰州诊断)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑,兰州市著名景点三台阁的屋顶部分也是典型的攒尖结构.某研究性学习小组制作的三台阁仿真模型的屋顶部分如图所示,它可以看作正三棱柱和不含下底面的正四棱台的组合体,已知正四棱台上、下底面边长(单位:dm)分别为2,6,侧棱的长度(单位:dm)为4,正三棱柱各棱长均相等,则该结构的表面积为( )
A.(34+8)dm2 B.(34+44)dm2
C.(34+48)dm2 D.(34+8)dm2
16.有一塔形组合体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是中层正方体上底面各边的中点,中层正方体下底面的四个顶点是最底层正方体上底面各边的中点.已知最底层正方体的棱长为2,求该塔形组合体的表面积.
17.(2022湖南长沙二十一中期中)如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5 cm,BC=16 cm,AD=4 cm.求:
(1)以AB所在直线为旋转轴旋转一周所得几何体的表面积;
(2)以BC所在直线为旋转轴旋转一周所得几何体的表面积.
能力提升练
题组一 几何体的表(侧)面积
1.(2022河南焦作期末)如图所示的正方体的棱长为2,则以其所有面的中心为顶点的多面体的表面积为( )
A.3 B.4 C.8 D.12
2.若底面是菱形的棱柱的侧棱垂直于底面,且侧棱长为5,它的体对角线的长分别是9和15,则这个棱柱的侧面积是( )
A.130 B.140 C.150 D.160
3.(2021云南昆明第一中学模拟)正三棱锥S-ABC中,若三条侧棱两两垂直,且顶点S到底面ABC的距离为,则这个正三棱锥的表面积为( )
A.3+ B.
C.2(3+) D.
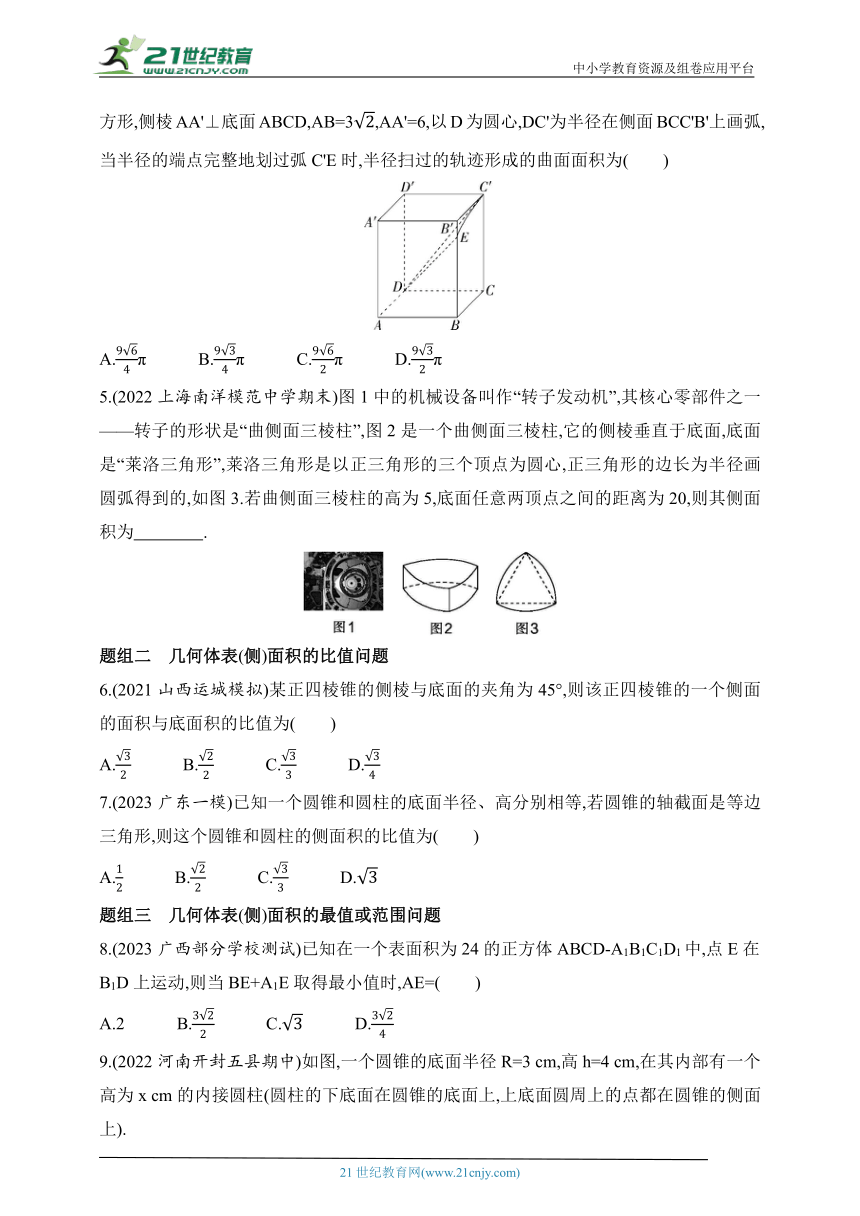
4.(2021江苏南京师范大学附属中学期中)如图,四棱柱ABCD-A'B'C'D'中,底面ABCD为正方形,侧棱AA'⊥底面ABCD,AB=3,AA'=6,以D为圆心,DC'为半径在侧面BCC'B'上画弧,当半径的端点完整地划过弧C'E时,半径扫过的轨迹形成的曲面面积为( )
A.π B.π C.π D.π
5.(2022上海南洋模范中学期末)图1中的机械设备叫作“转子发动机”,其核心零部件之一——转子的形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”,莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,如图3.若曲侧面三棱柱的高为5,底面任意两顶点之间的距离为20,则其侧面积为 .
题组二 几何体表(侧)面积的比值问题
6.(2021山西运城模拟)某正四棱锥的侧棱与底面的夹角为45°,则该正四棱锥的一个侧面的面积与底面积的比值为( )
A. B. C. D.
7.(2023广东一模)已知一个圆锥和圆柱的底面半径、高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的侧面积的比值为( )
A. B. C. D.
题组三 几何体表(侧)面积的最值或范围问题
8.(2023广西部分学校测试)已知在一个表面积为24的正方体ABCD-A1B1C1D1中,点E在B1D上运动,则当BE+A1E取得最小值时,AE=( )
A.2 B. C. D.
9.(2022河南开封五县期中)如图,一个圆锥的底面半径R=3 cm,高h=4 cm,在其内部有一个高为x cm的内接圆柱(圆柱的下底面在圆锥的底面上,上底面圆周上的点都在圆锥的侧面上).
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大 求出最大面积.
10.如图,有两个相同的直三棱柱,高均为,底面三角形的三边长分别为3a,4a,5a(a>0).用这两个三棱柱拼成一个三棱柱或四棱柱,若在所有可能的情形中,表面积最小的是一个四棱柱,求a的取值范围.
题组四 与几何体侧面展开图有关的最短路径问题
11.如图所示,圆柱的底面周长为12,高为2,矩形ABCD所在平面是该圆柱的轴截面,则在此圆柱的侧面上,从A到C的路径中,最短路径的长度为 ( )
A.2 B.2 C.3 D.2
12.(2021东北三省四市教研联合体联考)已知长方体ABCD-A1B1C1D1中,AB=2BC=4,E是C1D1的中点,且异面直线AD1与CE的夹角是60°,则在此长方体的表面上,从A1到C的路径中,最短路径的长度为 .
13.(2023上海复旦大学附属中学开学考试)如图所示,已知圆锥的底面半径r=2 m,经过旋转轴SO的截面是等边三角形SAB,Q为半圆弧的中点,P为母线SA的中点.若一只蚂蚁从Q点沿着圆锥的侧面爬至P点,你能否作出合情的假设,来估算该蚂蚁行程的最小值(精确到0.01 m).
答案与分层梯度式解析
第六章 立体几何初步
§6 简单几何体的再认识
6.1 柱、锥、台的侧面展开与面积
基础过关练
1.C 2.D 3.B 7.A 8.D 9.C 10.A 11.B
15.A
1.C 由题意得圆柱的轴截面是边长为10的正方形,所以圆柱的底面半径为5,母线长为10,
所以侧面积为2π×5×10=100π.故选C.
2.D 设圆台的母线长为l,
∵圆台的侧面积为3π,
∴πl×(1+2)=3πl=3π,解得l=,
设截去的圆锥的母线长为l',
由三角形相似可得,则2l'=l'+,解得l'=,
∴原圆锥的母线长为l'+l=.故选D.
3.B 若绕该三角形一直角边所在直线旋转一周,则所形成的几何体是圆锥,该圆锥的底面半径r=1,高h=1,母线长就是直角三角形的斜边长,记其为l,则l=,
故所形成的几何体的表面积S=πrl+πr2=π×1×)π;
若绕该三角形的斜边所在直线旋转一周,则所形成的几何体是上、下两个圆锥的组合体,上、下两个圆锥的底面半径都是直角三角形斜边上的高,记其为R,则R=,
上、下两个圆锥的母线长都是直角三角形的直角边的长,设母线长为L,则L=1,
故所形成的几何体的表面积S'=2πRL=2π×π.
综上所述,所形成的几何体的表面积为π或(1+)π.
4.答案
解析 设圆锥的底面半径为r,高为h,母线长为l,则圆锥的侧面积为πrl,过轴的截面面积为rh,∵圆锥的侧面积与过轴的截面面积的比值为2π,∴=2π,∴l=2h,
设母线与轴的夹角为θ,则cos θ=,故θ=.
5.答案
解析 如图所示,O为底面圆心,OC=2,OD⊥AC,则OD=1,
在△AOC中,由面积相等可知·AC·OD=·AO·OC,即AC=2AO,
又因为AC2=AO2+OC2,即(2AO)2=AO2+4,
所以AC=2AO=,
则该圆锥的侧面积S=π·OC·AC=π×2×.
方法总结 圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形,圆柱、圆锥、圆台的表面积包括侧面积与底面积.
6.解析 设圆柱的底面半径为R,高为h,则圆锥的底面半径为R,高为h,
设圆锥的母线长为l,则l=.
依题意,得2πRh=6,πRl=5,
所以R=,即圆柱的底面半径为.
7.A 所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22.故选A.
8.D 正四棱台的斜高h'=(cm),所以棱台的侧面积S=4×(cm2).
9.C 因为底面水平放置的直观图是边长为1的正方形,所以底面是一组邻边长分别为1与3,且长为1的边上的高为2的平行四边形,其周长是1+3+1+3=8,面积是1×2,所以直四棱柱的表面积是8×2+2.
10.A 如图,取AB的中点D,连接PD,CD.
设PO⊥底面ABC,垂足为O,则O在CD上,且OD==2.
因为PO=1,所以PD=,故该正三棱锥的侧面积为3×.故选A.
方法总结 多面体中的有关计算通常转化到平面图形(三角形或特殊的四边形)来解决,棱锥中的计算问题往往要构造直角三角形,即棱锥的高、斜高以及斜高在底面上的投影构成的直角三角形,或由棱锥的高、侧棱以及侧棱在底面上的投影构成的直角三角形.
11.B 如图所示,设该正四棱锥P-ABCD的高为h,底面边长为a,底面中心为O,侧面三角形底边上的高为h',
因为侧面三角形底边上的高与底面正方形边长的比值为,且h2+=h'2,
所以h2=h'2-.
该正四棱锥的侧面积S侧=4×h'a=2h'a,以该正四棱锥的高为边长的正方形的面积S正=h2,
所以.
故选B.
12.答案 2(答案不唯一)
解析 如图,可取三条侧棱长均为2,底面边长BC=BD=2,CD=1.
该四面体的表面积为2×.
13.解析 如图,设正六棱柱ABCDEF-A'B'C'D'E'F'的底面边长为a,侧棱长(即正六棱柱的高)为h,
易知CF'是此正六棱柱的一条最长的体对角线,
且CF'==13.①
因为正六棱柱的侧面积为180,
所以S侧=6a·h=180.②
联立①②,解得负值均舍去.
当a=6时,正六棱柱的底面积S底=6×,
所以S表=180+2×54.
当a=时,正六棱柱的底面积S底=6×,
所以S表=180+2×.
综上,此正六棱柱的表面积为180+108或180+.
14.解析 (1)证明:因为E,F分别是AB,AP的中点,
所以EF是△ABP的中位线,所以EF∥PB,
因为EF 平面PBC,PB 平面PBC,
所以EF∥平面PBC.
(2)若三棱锥P-ABC的各棱长均为2,则该三棱锥为正四面体,四个面是全等的等边三角形,
故它的表面积为4×.
15.A 由已知得,正三棱柱的一个底面积为×2×2×sin 60°=(dm2),
正三棱柱的外露表面积为2×(dm2),
正四棱台侧面梯形的高为(dm),
正四棱台的外露表面积为4×(dm2),
故该结构的表面积为32+8)dm2.
16.解析 易知由下到上三个正方体的棱长依次为2,,1.
考虑该几何体在水平面上的投影,可知其在水平面上的投影面积与最大正方体的一个底面的面积相等,∴S表=2×22+4×[22+()2+12]=36.
∴该塔形组合体的表面积为36.
17.解析 (1)以AB所在直线为旋转轴旋转一周所得几何体是圆台,其上底面半径是4 cm,下底面半径是16 cm,母线DC的长为=13(cm).
∴该几何体的表面积为π×(4+16)×13+π×42+π×162=532π(cm2).
(2)以BC所在直线为旋转轴旋转一周所得几何体是圆柱和圆锥的组合体,如图所示.其中圆锥的高为16-4=12(cm),由(1)可知圆锥的母线DC的长为13 cm,又圆柱的母线AD的长为4 cm,故该几何体的表面积为2π×5×4+π×52+π×5×13=130π(cm2).
方法总结 三类几何体表面积的求法
(1)多面体的表面积:只需将它们沿着某条棱“剪开”,展开成平面图形,利用求平面图形面积的方法求多面体的表面积;
(2)求旋转体的表面积:可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要弄清其底面半径、母线长与对应侧面展开图中的边长关系;
(3)不规则几何体的表面积:通常将不规则几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出不规则几何体的表面积.
能力提升练
1.B 2.D 3.D 4.A 6.D 7.C 8.A 11.A
1.B 由题意知,该几何体是一个由8个全等的正三角形围成的多面体,且正三角形的边长为,
所以一个正三角形的面积为,
所以多面体的表面积为8×.
2.D 如图,设直四棱柱ABCD-A1B1C1D1中,底面对角线AC=a,BD=b,交点为O,体对角线A1C=15,B1D=9,∴a2+52=152,b2+52=92,
∴a2=200,b2=56.∵该直四棱柱的底面是菱形,∴AB2==64,∴AB=8.
∴此直四棱柱的侧面积S=4×8×5=160.
3.D 设正三棱锥S-ABC的侧棱长为a,顶点S在底面ABC上的射影为O,则O为等边△ABC的中心.
因为SA,SB,SC两两垂直,且SA=SB=SC=a,所以AB=AC=BC=a,
等边△ABC的外接圆的半径为OC=a,
由勾股定理可得SO2+OC2=SC2,
即3+a2=a2,
解得a=3(负值舍去),
所以正三棱锥S-ABC的表面积为3×.故选D.
4.A 连接EC,由题意得半径扫过的轨迹形成的曲面是以D为顶点,C为底面圆心,DC'为母线的圆锥的侧面的一部分,则CE=CC'=AA'=6,DE=DC'=,
连接BD,则BD⊥BE,又四边形ABCD是正方形,所以BD=AB=6,所以BE==BC,所以∠BCE=,所以∠ECC'=,
又,所以曲面面积是该圆锥的侧面积的,
又圆锥的侧面积S=π×CC'×DC'=π×6×3π,
所以曲面面积为18π.故选A.
5.答案 100π
解析 如图所示,由题意得△ABC为等边三角形,且边长为20,
所以弧的长度l=,
曲侧面三棱柱的三个侧面展开后均是长为,宽为5的矩形,
所以曲侧面三棱柱的侧面积为3××5=100π.
6.D 如图,PO是正四棱锥P-ABCD的高,
设底面边长为a,则底面积S1=a2,
因为正四棱锥的侧棱与底面的夹角为45°,所以∠PAO=45°,又AO=a,所以PA=a=a,
所以PA=PB=AB,
所以△PAB是正三角形,其面积S2=a2,
所以正四棱锥的一个侧面的面积与底面积的比值为.故选D.
7.C 设圆锥和圆柱的底面半径均为r,
因为圆锥的轴截面是等边三角形,所以圆锥的母线长l=2r,
则圆锥和圆柱的高h=r,
所以圆锥的侧面积S1=πrl=2πr2,
圆柱的侧面积S2=2πrh=2πr2,
所以这个圆锥和圆柱的侧面积的比值为.
8.A 作出图形如下:
依题意知6AB2=24,故AB=2.
连接A1D,BD,
易得△A1B1D≌△BB1D,所以过A1作B1D的垂线交B1D的点与过B作B1D的垂线交B1D的点重合,
所以当A1E⊥B1D且BE⊥B1D时,BE+A1E取得最小值,此时.
过点E作平面ABCD的垂线,垂足为F,易知F在BD上,连接AF,在△ABF中,由余弦定理得,AF2=AB2+BF2-2AB·BF·cos 45°=4+,
则AE==2.
9.解析 (1)圆锥的母线长l==5(cm),
所以圆锥的侧面积S侧=πRl=π×3×5=15π(cm2).
(2)设圆柱的底面半径为r cm,圆柱的侧面积为S cm2,
由题意得,即,所以r=3-x(0所以S=2πr·x=·(-x2+4x)=·[-(x-2)2+4](0即当x=2时,圆柱的侧面积最大,最大面积为6π cm2.
10.解析 所给直三棱柱的底面积为6a2,侧面的面积分别为6,8,10.当拼成三棱柱时有三种情况,分别如图①、图②、图③所示,表面积分别为S1=2×6a2+2×(10+8+6)=12a2+48,S2=4×6a2+2×(10+8)=24a2+36,S3=4×6a2+2×(10+6)=24a2+32.
当拼成四棱柱时有四种情况,分别如图④、图⑤、图⑥、图⑦所示,表面积分别为S4=S7=24a2+2×(8+6)=24a2+28,S5=24a2+2×(10+8)=24a2+36,S6=24a2+2×(10+6)=24a2+32.
由题意得24a2+28<12a2+48,
所以011.A 如图,圆柱的侧面展开图是矩形,且矩形的长为12,宽为2,则在此圆柱的侧面上从A到C的最短路径为线段AC,易得AC=.故选A.
12.答案 4
解析 如图,取CD的中点F,连接D1F,AF,
易得D1E∥CF且D1E=CF,则四边形D1ECF为平行四边形,所以D1F∥CE,则∠AD1F(或其补角)即为异面直线AD1与CE的夹角,易知
∠AD1F为锐角,则∠AD1F=60°.
设AA1=a,则A,
则cos∠AD1F=,
所以a=2(负值舍去).
(1)将面ABB1A1和面BCC1B1展开如图,
此时从A1到C的路径中,最短路径的长度为.
(2)将面A1B1C1D1和面B1BCC1展开如图,
此时从A1到C的路径中,最短路径的长度为.
(3)将面A1B1C1D1和面D1C1CD展开如图,
此时从A1到C的路径中,最短路径的长度为.
综上,从A1到C的路径中,最短路径的长度为4.
13.解析 将母线SQ,SA及劣弧围成的曲面展开,如图,连接PQ,
则l ×2πr=π,∠ASQ=,
在△SPQ中,由余弦定理可得,
PQ2=SP2+SQ2-2SP·SQcos∠ASQ=20-8,
所以PQ=≈2.95(m).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版高中数学必修第二册同步练习题
第六章 立体几何初步
§6 简单几何体的再认识
6.1 柱、锥、台的侧面展开与面积
基础过关练
题组一 圆柱、圆锥、圆台的表(侧)面积
1.(2022河南焦作二模)已知圆柱的轴截面是面积为100的正方形,则该圆柱的侧面积为( )
A.50π B.200
C.100π D.150π
2.(2023云南昆明三中适应性考试)用一个平行于圆锥底面的平面去截圆锥,截得的圆台的上底面半径为1,下底面半径为2,且该圆台的侧面积为3π,则原圆锥的母线长为( )
A.2 B. C.4 D.2
3.(2023河北邯郸鸡泽第一中学月考)已知某等腰直角三角形的直角边长为1,现将该三角形绕其某一边所在直线旋转一周,则所形成的几何体的表面积为( )
A.π B.π或(1+)π
C.2π D.2π或(2+)π
4.(2023湖南邵阳邵东四中期中)若圆锥的侧面积与过轴的截面面积的比值为2π,则其母线与轴的夹角的大小为 .
5.(2023上海四校联考)已知圆锥的底面半径为2,底面圆心到某条母线的距离为1,则该圆锥的侧面积为 .
6.以圆柱的上底中心为顶点,下底面为底面作圆锥,假设圆柱的侧面积为6,圆锥的侧面积为5,求圆柱的底面半径.
题组二 棱柱、棱锥、棱台的表(侧)面积
7.已知某长方体同一顶点上的三条棱的长分别为1,2,3,则该长方体的表面积为( )
A.22 B.20 C.10 D.11
8.(2022重庆十一中月考)正四棱台的上底面边长a=2 cm,下底面边长b=4 cm,侧棱长l=2 cm,则棱台的侧面积为( )
A.6 cm2 B.24 cm2
C.3 cm2 D.12 cm2
9.(2022重庆渝东六校共同体期中)已知一个直四棱柱的高为2,其底面水平放置的直观图(用斜二测画法画出)是边长为1的正方形,则这个直四棱柱的表面积为( )
A.10 B.8+4
C.16+4 D.16+4
10.若正三棱锥P-ABC的高为1,AB=4,则该正三棱锥的侧面积为( )
A.6 B.18 C.6 D.6
11.(2023浙江北斗联盟期中)由华裔建筑师贝聿铭设计的巴黎卢浮宫玻璃金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),其侧面三角形底边上的高与底面正方形边长的比值为,则以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为( )
A.2 B.
C. D.4
12.(2023北京第一六六中学期中)若四面体各棱的长是1或2,且该四面体不是正四面体,则其表面积可能是 .(只需写出一个可能的值)
13.正六棱柱的一条最长的体对角线长是13,侧面积为180,求此正六棱柱的表面积.
14.(2022重庆巫山官渡中学月考)如图,在三棱锥P-ABC中,E,F分别是AB,AP的中点.
(1)求证:EF∥平面PBC;
(2)若三棱锥P-ABC的各棱长均为2,求它的表面积.
题组三 组合体的表(侧)面积
15.(2023甘肃兰州诊断)攒尖是中国古建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多见于亭阁式建筑,兰州市著名景点三台阁的屋顶部分也是典型的攒尖结构.某研究性学习小组制作的三台阁仿真模型的屋顶部分如图所示,它可以看作正三棱柱和不含下底面的正四棱台的组合体,已知正四棱台上、下底面边长(单位:dm)分别为2,6,侧棱的长度(单位:dm)为4,正三棱柱各棱长均相等,则该结构的表面积为( )
A.(34+8)dm2 B.(34+44)dm2
C.(34+48)dm2 D.(34+8)dm2
16.有一塔形组合体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是中层正方体上底面各边的中点,中层正方体下底面的四个顶点是最底层正方体上底面各边的中点.已知最底层正方体的棱长为2,求该塔形组合体的表面积.
17.(2022湖南长沙二十一中期中)如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5 cm,BC=16 cm,AD=4 cm.求:
(1)以AB所在直线为旋转轴旋转一周所得几何体的表面积;
(2)以BC所在直线为旋转轴旋转一周所得几何体的表面积.
能力提升练
题组一 几何体的表(侧)面积
1.(2022河南焦作期末)如图所示的正方体的棱长为2,则以其所有面的中心为顶点的多面体的表面积为( )
A.3 B.4 C.8 D.12
2.若底面是菱形的棱柱的侧棱垂直于底面,且侧棱长为5,它的体对角线的长分别是9和15,则这个棱柱的侧面积是( )
A.130 B.140 C.150 D.160
3.(2021云南昆明第一中学模拟)正三棱锥S-ABC中,若三条侧棱两两垂直,且顶点S到底面ABC的距离为,则这个正三棱锥的表面积为( )
A.3+ B.
C.2(3+) D.
4.(2021江苏南京师范大学附属中学期中)如图,四棱柱ABCD-A'B'C'D'中,底面ABCD为正方形,侧棱AA'⊥底面ABCD,AB=3,AA'=6,以D为圆心,DC'为半径在侧面BCC'B'上画弧,当半径的端点完整地划过弧C'E时,半径扫过的轨迹形成的曲面面积为( )
A.π B.π C.π D.π
5.(2022上海南洋模范中学期末)图1中的机械设备叫作“转子发动机”,其核心零部件之一——转子的形状是“曲侧面三棱柱”,图2是一个曲侧面三棱柱,它的侧棱垂直于底面,底面是“莱洛三角形”,莱洛三角形是以正三角形的三个顶点为圆心,正三角形的边长为半径画圆弧得到的,如图3.若曲侧面三棱柱的高为5,底面任意两顶点之间的距离为20,则其侧面积为 .
题组二 几何体表(侧)面积的比值问题
6.(2021山西运城模拟)某正四棱锥的侧棱与底面的夹角为45°,则该正四棱锥的一个侧面的面积与底面积的比值为( )
A. B. C. D.
7.(2023广东一模)已知一个圆锥和圆柱的底面半径、高分别相等,若圆锥的轴截面是等边三角形,则这个圆锥和圆柱的侧面积的比值为( )
A. B. C. D.
题组三 几何体表(侧)面积的最值或范围问题
8.(2023广西部分学校测试)已知在一个表面积为24的正方体ABCD-A1B1C1D1中,点E在B1D上运动,则当BE+A1E取得最小值时,AE=( )
A.2 B. C. D.
9.(2022河南开封五县期中)如图,一个圆锥的底面半径R=3 cm,高h=4 cm,在其内部有一个高为x cm的内接圆柱(圆柱的下底面在圆锥的底面上,上底面圆周上的点都在圆锥的侧面上).
(1)求圆锥的侧面积;
(2)当x为何值时,圆柱的侧面积最大 求出最大面积.
10.如图,有两个相同的直三棱柱,高均为,底面三角形的三边长分别为3a,4a,5a(a>0).用这两个三棱柱拼成一个三棱柱或四棱柱,若在所有可能的情形中,表面积最小的是一个四棱柱,求a的取值范围.
题组四 与几何体侧面展开图有关的最短路径问题
11.如图所示,圆柱的底面周长为12,高为2,矩形ABCD所在平面是该圆柱的轴截面,则在此圆柱的侧面上,从A到C的路径中,最短路径的长度为 ( )
A.2 B.2 C.3 D.2
12.(2021东北三省四市教研联合体联考)已知长方体ABCD-A1B1C1D1中,AB=2BC=4,E是C1D1的中点,且异面直线AD1与CE的夹角是60°,则在此长方体的表面上,从A1到C的路径中,最短路径的长度为 .
13.(2023上海复旦大学附属中学开学考试)如图所示,已知圆锥的底面半径r=2 m,经过旋转轴SO的截面是等边三角形SAB,Q为半圆弧的中点,P为母线SA的中点.若一只蚂蚁从Q点沿着圆锥的侧面爬至P点,你能否作出合情的假设,来估算该蚂蚁行程的最小值(精确到0.01 m).
答案与分层梯度式解析
第六章 立体几何初步
§6 简单几何体的再认识
6.1 柱、锥、台的侧面展开与面积
基础过关练
1.C 2.D 3.B 7.A 8.D 9.C 10.A 11.B
15.A
1.C 由题意得圆柱的轴截面是边长为10的正方形,所以圆柱的底面半径为5,母线长为10,
所以侧面积为2π×5×10=100π.故选C.
2.D 设圆台的母线长为l,
∵圆台的侧面积为3π,
∴πl×(1+2)=3πl=3π,解得l=,
设截去的圆锥的母线长为l',
由三角形相似可得,则2l'=l'+,解得l'=,
∴原圆锥的母线长为l'+l=.故选D.
3.B 若绕该三角形一直角边所在直线旋转一周,则所形成的几何体是圆锥,该圆锥的底面半径r=1,高h=1,母线长就是直角三角形的斜边长,记其为l,则l=,
故所形成的几何体的表面积S=πrl+πr2=π×1×)π;
若绕该三角形的斜边所在直线旋转一周,则所形成的几何体是上、下两个圆锥的组合体,上、下两个圆锥的底面半径都是直角三角形斜边上的高,记其为R,则R=,
上、下两个圆锥的母线长都是直角三角形的直角边的长,设母线长为L,则L=1,
故所形成的几何体的表面积S'=2πRL=2π×π.
综上所述,所形成的几何体的表面积为π或(1+)π.
4.答案
解析 设圆锥的底面半径为r,高为h,母线长为l,则圆锥的侧面积为πrl,过轴的截面面积为rh,∵圆锥的侧面积与过轴的截面面积的比值为2π,∴=2π,∴l=2h,
设母线与轴的夹角为θ,则cos θ=,故θ=.
5.答案
解析 如图所示,O为底面圆心,OC=2,OD⊥AC,则OD=1,
在△AOC中,由面积相等可知·AC·OD=·AO·OC,即AC=2AO,
又因为AC2=AO2+OC2,即(2AO)2=AO2+4,
所以AC=2AO=,
则该圆锥的侧面积S=π·OC·AC=π×2×.
方法总结 圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形,圆柱、圆锥、圆台的表面积包括侧面积与底面积.
6.解析 设圆柱的底面半径为R,高为h,则圆锥的底面半径为R,高为h,
设圆锥的母线长为l,则l=.
依题意,得2πRh=6,πRl=5,
所以R=,即圆柱的底面半径为.
7.A 所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22.故选A.
8.D 正四棱台的斜高h'=(cm),所以棱台的侧面积S=4×(cm2).
9.C 因为底面水平放置的直观图是边长为1的正方形,所以底面是一组邻边长分别为1与3,且长为1的边上的高为2的平行四边形,其周长是1+3+1+3=8,面积是1×2,所以直四棱柱的表面积是8×2+2.
10.A 如图,取AB的中点D,连接PD,CD.
设PO⊥底面ABC,垂足为O,则O在CD上,且OD==2.
因为PO=1,所以PD=,故该正三棱锥的侧面积为3×.故选A.
方法总结 多面体中的有关计算通常转化到平面图形(三角形或特殊的四边形)来解决,棱锥中的计算问题往往要构造直角三角形,即棱锥的高、斜高以及斜高在底面上的投影构成的直角三角形,或由棱锥的高、侧棱以及侧棱在底面上的投影构成的直角三角形.
11.B 如图所示,设该正四棱锥P-ABCD的高为h,底面边长为a,底面中心为O,侧面三角形底边上的高为h',
因为侧面三角形底边上的高与底面正方形边长的比值为,且h2+=h'2,
所以h2=h'2-.
该正四棱锥的侧面积S侧=4×h'a=2h'a,以该正四棱锥的高为边长的正方形的面积S正=h2,
所以.
故选B.
12.答案 2(答案不唯一)
解析 如图,可取三条侧棱长均为2,底面边长BC=BD=2,CD=1.
该四面体的表面积为2×.
13.解析 如图,设正六棱柱ABCDEF-A'B'C'D'E'F'的底面边长为a,侧棱长(即正六棱柱的高)为h,
易知CF'是此正六棱柱的一条最长的体对角线,
且CF'==13.①
因为正六棱柱的侧面积为180,
所以S侧=6a·h=180.②
联立①②,解得负值均舍去.
当a=6时,正六棱柱的底面积S底=6×,
所以S表=180+2×54.
当a=时,正六棱柱的底面积S底=6×,
所以S表=180+2×.
综上,此正六棱柱的表面积为180+108或180+.
14.解析 (1)证明:因为E,F分别是AB,AP的中点,
所以EF是△ABP的中位线,所以EF∥PB,
因为EF 平面PBC,PB 平面PBC,
所以EF∥平面PBC.
(2)若三棱锥P-ABC的各棱长均为2,则该三棱锥为正四面体,四个面是全等的等边三角形,
故它的表面积为4×.
15.A 由已知得,正三棱柱的一个底面积为×2×2×sin 60°=(dm2),
正三棱柱的外露表面积为2×(dm2),
正四棱台侧面梯形的高为(dm),
正四棱台的外露表面积为4×(dm2),
故该结构的表面积为32+8)dm2.
16.解析 易知由下到上三个正方体的棱长依次为2,,1.
考虑该几何体在水平面上的投影,可知其在水平面上的投影面积与最大正方体的一个底面的面积相等,∴S表=2×22+4×[22+()2+12]=36.
∴该塔形组合体的表面积为36.
17.解析 (1)以AB所在直线为旋转轴旋转一周所得几何体是圆台,其上底面半径是4 cm,下底面半径是16 cm,母线DC的长为=13(cm).
∴该几何体的表面积为π×(4+16)×13+π×42+π×162=532π(cm2).
(2)以BC所在直线为旋转轴旋转一周所得几何体是圆柱和圆锥的组合体,如图所示.其中圆锥的高为16-4=12(cm),由(1)可知圆锥的母线DC的长为13 cm,又圆柱的母线AD的长为4 cm,故该几何体的表面积为2π×5×4+π×52+π×5×13=130π(cm2).
方法总结 三类几何体表面积的求法
(1)多面体的表面积:只需将它们沿着某条棱“剪开”,展开成平面图形,利用求平面图形面积的方法求多面体的表面积;
(2)求旋转体的表面积:可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要弄清其底面半径、母线长与对应侧面展开图中的边长关系;
(3)不规则几何体的表面积:通常将不规则几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出不规则几何体的表面积.
能力提升练
1.B 2.D 3.D 4.A 6.D 7.C 8.A 11.A
1.B 由题意知,该几何体是一个由8个全等的正三角形围成的多面体,且正三角形的边长为,
所以一个正三角形的面积为,
所以多面体的表面积为8×.
2.D 如图,设直四棱柱ABCD-A1B1C1D1中,底面对角线AC=a,BD=b,交点为O,体对角线A1C=15,B1D=9,∴a2+52=152,b2+52=92,
∴a2=200,b2=56.∵该直四棱柱的底面是菱形,∴AB2==64,∴AB=8.
∴此直四棱柱的侧面积S=4×8×5=160.
3.D 设正三棱锥S-ABC的侧棱长为a,顶点S在底面ABC上的射影为O,则O为等边△ABC的中心.
因为SA,SB,SC两两垂直,且SA=SB=SC=a,所以AB=AC=BC=a,
等边△ABC的外接圆的半径为OC=a,
由勾股定理可得SO2+OC2=SC2,
即3+a2=a2,
解得a=3(负值舍去),
所以正三棱锥S-ABC的表面积为3×.故选D.
4.A 连接EC,由题意得半径扫过的轨迹形成的曲面是以D为顶点,C为底面圆心,DC'为母线的圆锥的侧面的一部分,则CE=CC'=AA'=6,DE=DC'=,
连接BD,则BD⊥BE,又四边形ABCD是正方形,所以BD=AB=6,所以BE==BC,所以∠BCE=,所以∠ECC'=,
又,所以曲面面积是该圆锥的侧面积的,
又圆锥的侧面积S=π×CC'×DC'=π×6×3π,
所以曲面面积为18π.故选A.
5.答案 100π
解析 如图所示,由题意得△ABC为等边三角形,且边长为20,
所以弧的长度l=,
曲侧面三棱柱的三个侧面展开后均是长为,宽为5的矩形,
所以曲侧面三棱柱的侧面积为3××5=100π.
6.D 如图,PO是正四棱锥P-ABCD的高,
设底面边长为a,则底面积S1=a2,
因为正四棱锥的侧棱与底面的夹角为45°,所以∠PAO=45°,又AO=a,所以PA=a=a,
所以PA=PB=AB,
所以△PAB是正三角形,其面积S2=a2,
所以正四棱锥的一个侧面的面积与底面积的比值为.故选D.
7.C 设圆锥和圆柱的底面半径均为r,
因为圆锥的轴截面是等边三角形,所以圆锥的母线长l=2r,
则圆锥和圆柱的高h=r,
所以圆锥的侧面积S1=πrl=2πr2,
圆柱的侧面积S2=2πrh=2πr2,
所以这个圆锥和圆柱的侧面积的比值为.
8.A 作出图形如下:
依题意知6AB2=24,故AB=2.
连接A1D,BD,
易得△A1B1D≌△BB1D,所以过A1作B1D的垂线交B1D的点与过B作B1D的垂线交B1D的点重合,
所以当A1E⊥B1D且BE⊥B1D时,BE+A1E取得最小值,此时.
过点E作平面ABCD的垂线,垂足为F,易知F在BD上,连接AF,在△ABF中,由余弦定理得,AF2=AB2+BF2-2AB·BF·cos 45°=4+,
则AE==2.
9.解析 (1)圆锥的母线长l==5(cm),
所以圆锥的侧面积S侧=πRl=π×3×5=15π(cm2).
(2)设圆柱的底面半径为r cm,圆柱的侧面积为S cm2,
由题意得,即,所以r=3-x(0
10.解析 所给直三棱柱的底面积为6a2,侧面的面积分别为6,8,10.当拼成三棱柱时有三种情况,分别如图①、图②、图③所示,表面积分别为S1=2×6a2+2×(10+8+6)=12a2+48,S2=4×6a2+2×(10+8)=24a2+36,S3=4×6a2+2×(10+6)=24a2+32.
当拼成四棱柱时有四种情况,分别如图④、图⑤、图⑥、图⑦所示,表面积分别为S4=S7=24a2+2×(8+6)=24a2+28,S5=24a2+2×(10+8)=24a2+36,S6=24a2+2×(10+6)=24a2+32.
由题意得24a2+28<12a2+48,
所以0
12.答案 4
解析 如图,取CD的中点F,连接D1F,AF,
易得D1E∥CF且D1E=CF,则四边形D1ECF为平行四边形,所以D1F∥CE,则∠AD1F(或其补角)即为异面直线AD1与CE的夹角,易知
∠AD1F为锐角,则∠AD1F=60°.
设AA1=a,则A,
则cos∠AD1F=,
所以a=2(负值舍去).
(1)将面ABB1A1和面BCC1B1展开如图,
此时从A1到C的路径中,最短路径的长度为.
(2)将面A1B1C1D1和面B1BCC1展开如图,
此时从A1到C的路径中,最短路径的长度为.
(3)将面A1B1C1D1和面D1C1CD展开如图,
此时从A1到C的路径中,最短路径的长度为.
综上,从A1到C的路径中,最短路径的长度为4.
13.解析 将母线SQ,SA及劣弧围成的曲面展开,如图,连接PQ,
则l ×2πr=π,∠ASQ=,
在△SPQ中,由余弦定理可得,
PQ2=SP2+SQ2-2SP·SQcos∠ASQ=20-8,
所以PQ=≈2.95(m).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
