2024北师版高中数学必修第二册同步练习题--6.2 平面向量在几何、物理中的应用举例(含解析)
文档属性
| 名称 | 2024北师版高中数学必修第二册同步练习题--6.2 平面向量在几何、物理中的应用举例(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 21:26:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师版高中数学必修第二册同步练习题
第二章 平面向量及其应用
6.2 平面向量在几何、物理中的应用举例
基础过关练
题组一 向量在几何证明中的应用
1.如图,平行四边形ABCD中,M是AB的中点,点N在BD上,且BN=BD,求证:M,N,C三点共线.
2.(2022山西晋中平遥第二中学校月考)用向量法证明:以A(1,0),B(5,
-2),C(8,4),D(4,6)为顶点的四边形是一个矩形.
题组二 向量在物理中的应用
3.(2023福建厦门第二中学阶段考试)某种礼物降落伞的示意图如图所示,其中有8根绳子和伞面连接,每根绳子和水平面的法线的夹角都为30°.已知该礼物的质量为10 kg,降落伞自身的质量为2 kg,每根绳子的拉力大小相同,则降落伞在匀速下落的过程中每根绳子拉力的大小为(重力加速度g取9.8 N/kg,≈1.732,计算结果精确到0.01 N)( )
A.1.41 N B.1.56 N C.16.97 N D.17.04 N
4.(2022浙江精诚联盟联考)甲、乙两人提起重量为8 N的物体,两人用力方向的夹角为θ,用力大小分别为6 N,7 N,则cos θ的值为( )
A.- B. C. D.-
5.(多选题)(2022浙江北斗联盟联考)在水流速度为4 km/h的河水中,一艘船以12 km/h的实际航行速度垂直于对岸行驶,则下列关于这艘船的航行速度的大小和方向的说法中,正确的是( )
A.这艘船航行速度的大小为12 km/h
B.这艘船航行速度的大小为8 km/h
C.这艘船航行速度的方向与水流方向的夹角为150°
D.这艘船航行速度的方向与水流方向的夹角为120°
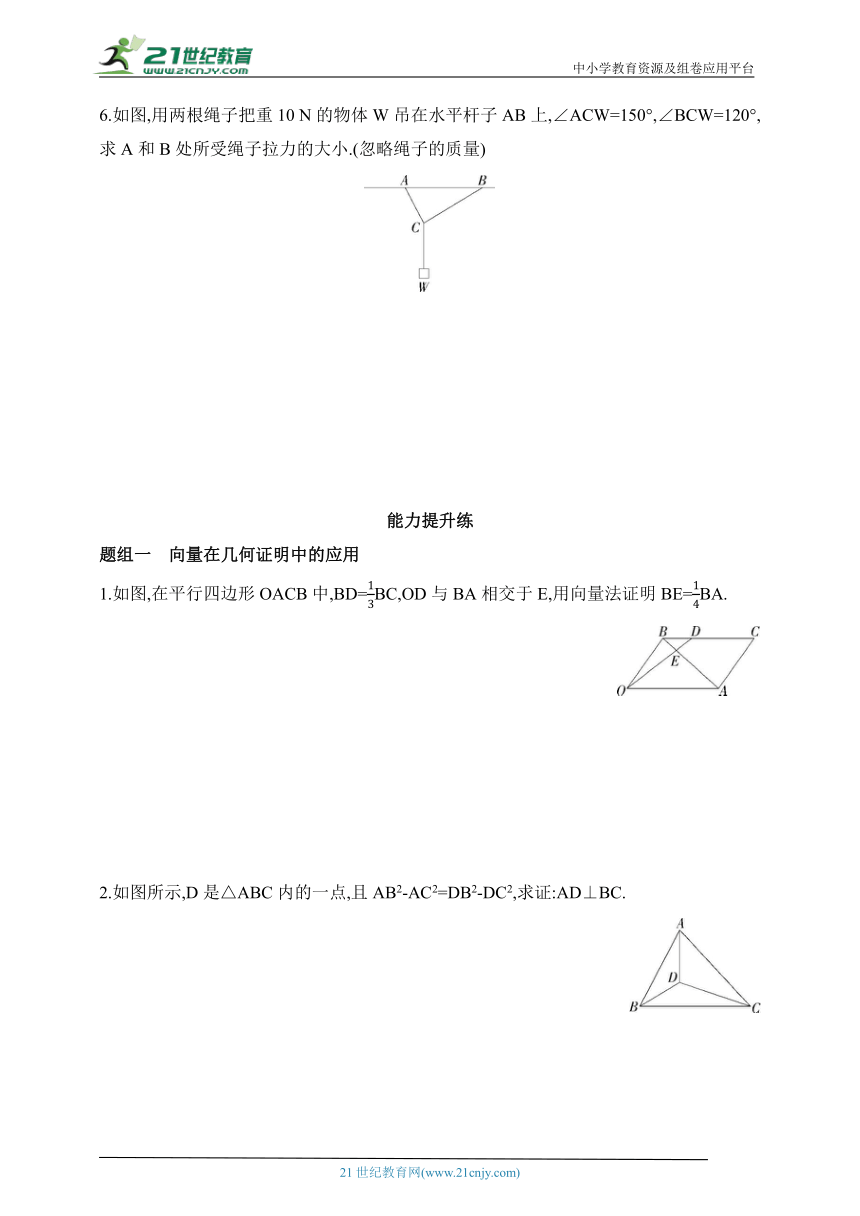
6.如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受绳子拉力的大小.(忽略绳子的质量)
能力提升练
题组一 向量在几何证明中的应用
1.如图,在平行四边形OACB中,BD=BC,OD与BA相交于E,用向量法证明BE=BA.
2.如图所示,D是△ABC内的一点,且AB2-AC2=DB2-DC2,求证:AD⊥BC.
3.已知矩形ABCD中,AB=3,BC=2,E为线段BC的中点,P为线段AB上一点.
(1)利用向量知识判断点P在什么位置时,∠PED=45°;
(2)若∠PED=45°,求证:D,P,E,C四点共圆.
题组二 向量在物理中的应用
4.(2022山东烟台第二中学期中)一条东西方向的河流两岸平行,河宽250 m,河水自西向东流,速度为3 km/h.一艘小货船准备从河南岸的码头P处出发,航行到河对岸的Q(PQ与河流的方向垂直)的正西方向并且与Q相距250 m的码头M处卸货,若水流的速度与小货船航行的速度的合速度的大小为5 km/h,则当小货船的航程最短时,小货船航行速度的大小为( )
A.3 km/h B.6 km/h
C.7 km/h D.3 km/h
5.当两人同提重|G|的书包时,用力大小都为|F|,两力的夹角为θ,且|F|,|G|,θ之间的关系为|F|=.当θ= 时,|F|取得最小值;当|F|=|G|时,θ= .
6.如图,在同一平面内,一个质点O受三个力F1,F2,F3的作用保持平衡,其中F3与F2的夹角为α,F3与F1的夹角为β.
(1)若α=120°,β=150°,|F3|=10,求力F1,F2的大小;
(2)若|F1|∶|F2|∶|F3|=1∶,求α与β的余弦值.
答案与分层梯度式解析
第二章 平面向量及其应用
6.2 平面向量在几何、物理中的应用举例
基础过关练
3.C 4.A 5.BD
1.证明 设=x,=y,
则y+y+(x-y)=(2x+y),
y+x=(2x+y),
∴,又MC与MN有公共点M,
∴M,N,C三点共线.
2.证明 由已知得=(4,-2),故,
又=(3,6)不为零向量,且不与平行,所以以A,B,C,D为顶点的四边形是平行四边形.又=4×3-2×6=0,所以,故以A,B,C,D为顶点的四边形是一个矩形.
3.C 设每根绳子拉力的大小为T N,礼物降落伞的总质量为m,
根据平衡条件可得,8T·cos 30°=mg,
解得T=≈16.97,
所以降落伞在匀速下落的过程中每根绳子拉力的大小约为16.97 N.故选C.
4.A 如图,设||=7,
合力的大小即为||=8,
将两边平方可得(,
即||2,
∴62+2×6×7×cos θ+72=82,解得cos θ=-.
5.BD 设船的实际航行速度为v1,水流速度为v2,船的航行速度为v3,
根据题意得|v3|= km/h,
设船的航行方向和水流方向的夹角为θ,90°<θ<180°,
则tan(180°-θ)=,
所以θ=120°,故选BD.
6.解析 设A,B处所受绳子的拉力分别为f1,f2,10 N的重力用f表示,则f1+f2=f.
如图,以重力作用点C为f1,f2的始点,作平行四边形CEWF,使CW为对角线,则=f1,=f2,=f,则∠FCW=180°-150°=30°,∠ECW=180°-120°=60°,
∴∠FCE=90°,∴四边形CEWF为矩形.
∴|f1|=||cos 30°=10×,
|f2|=||cos 60°=10×=5,
即A处受绳子拉力的大小为5 N,B处受绳子拉力的大小为5 N.
能力提升练
1.证明 设=a,=b,
则a,=b+a.
∵共线,
∴存在实数λ,使,
∴-b=a+(λ-1)b.
∵共线,
∴存在实数μ,使)=μ(a-b).
于是a+(λ-1)b=μ(a-b),
即a=(1-λ-μ)b.
∵a与b不共线,
∴
∴,即BE=BA.
2.证明 设=a,=b,=c,=d,=e,
则a=e+c,b=e+d,
所以a2-b2=(e+c)2-(e+d)2=c2+2e·c-2e·d-d2,
由题意得a2-b2=c2-d2,
所以e·c-e·d=0,即e·(c-d)=0,
即=0,所以,
所以AD⊥BC.
3.解析 (1)如图,建立平面直角坐标系,
则D(2,3),E(1,0),设P(0,y),0≤y≤3,
则=(-1,y),
∴|=3y-1,
∴cos 45°=,
解得y=2(负值舍去),
∴点P为线段AB上靠近点A的三等分点时,∠PED=45°.
(2)证明:连接DP,由(1)知当∠PED=45°时,P(0,2),
则=(-1,2),
∴=0,∴∠DPE=90°,
又∠DCE=90°,∴D,P,E,C四点在以DE为直径的圆上,即D,P,E,C四点共圆.
4.C 由题意知,当小货船的航程最短时,航线为线段PM,设小货船航行速度为v,水流的速度为v1,水流速度与小货船航行速度的合速度为v2,作出示意图如下:
由题知,PQ=250 m,QM=250 m,在Rt△PQM中,tan∠PMQ=,所以∠PMQ=,
所以∠MPQ=,=,
又v=v2-v1,
所以|v|==7,
所以小货船航行速度的大小为7 km/h,故选C.
5.答案 0;
解析 因为|F| =,
所以当cos =1,即θ=0时,|F|取得最小值.
当|F|=|G|时,cos ,此时θ=.
6.解析 (1)因为质点在F1,F2,F3的作用下保持平衡,所以F1+F2+F3=0,所以F3=-(F1+F2),
又α=120°,β=150°,
所以F1与F2的夹角为90°,所以F1·F2=0,
则|F3|2=[-(F1+F2)]2=+2F1·F2+,
将|F3|=10代入可得=100.
如图.
易得∠1=30°, 所以|F1|=|F3|×cos 30°=10×,
|F2|=|F3|×sin 30°=10×=5.
(2)因为|F1|∶|F2|∶|F3|=1∶,且质点处于平衡状态,
所以以|F1|,|F2|,|F3|为边长的三角形为直角三角形,如图所示,
则cos∠3=,cos∠2=,
所以cos β=cos(π-∠3)=-cos∠3=-,
cos α=cos(π-∠2)=-cos∠2=-.
方法总结 用数学知识解决物理问题时,首先要把物理问题转化为数学问题,也就是将物理量之间的关系抽象成数学模型,然后通过对这个数学模型的研究解释相关的物理现象.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版高中数学必修第二册同步练习题
第二章 平面向量及其应用
6.2 平面向量在几何、物理中的应用举例
基础过关练
题组一 向量在几何证明中的应用
1.如图,平行四边形ABCD中,M是AB的中点,点N在BD上,且BN=BD,求证:M,N,C三点共线.
2.(2022山西晋中平遥第二中学校月考)用向量法证明:以A(1,0),B(5,
-2),C(8,4),D(4,6)为顶点的四边形是一个矩形.
题组二 向量在物理中的应用
3.(2023福建厦门第二中学阶段考试)某种礼物降落伞的示意图如图所示,其中有8根绳子和伞面连接,每根绳子和水平面的法线的夹角都为30°.已知该礼物的质量为10 kg,降落伞自身的质量为2 kg,每根绳子的拉力大小相同,则降落伞在匀速下落的过程中每根绳子拉力的大小为(重力加速度g取9.8 N/kg,≈1.732,计算结果精确到0.01 N)( )
A.1.41 N B.1.56 N C.16.97 N D.17.04 N
4.(2022浙江精诚联盟联考)甲、乙两人提起重量为8 N的物体,两人用力方向的夹角为θ,用力大小分别为6 N,7 N,则cos θ的值为( )
A.- B. C. D.-
5.(多选题)(2022浙江北斗联盟联考)在水流速度为4 km/h的河水中,一艘船以12 km/h的实际航行速度垂直于对岸行驶,则下列关于这艘船的航行速度的大小和方向的说法中,正确的是( )
A.这艘船航行速度的大小为12 km/h
B.这艘船航行速度的大小为8 km/h
C.这艘船航行速度的方向与水流方向的夹角为150°
D.这艘船航行速度的方向与水流方向的夹角为120°
6.如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW=150°,∠BCW=120°,求A和B处所受绳子拉力的大小.(忽略绳子的质量)
能力提升练
题组一 向量在几何证明中的应用
1.如图,在平行四边形OACB中,BD=BC,OD与BA相交于E,用向量法证明BE=BA.
2.如图所示,D是△ABC内的一点,且AB2-AC2=DB2-DC2,求证:AD⊥BC.
3.已知矩形ABCD中,AB=3,BC=2,E为线段BC的中点,P为线段AB上一点.
(1)利用向量知识判断点P在什么位置时,∠PED=45°;
(2)若∠PED=45°,求证:D,P,E,C四点共圆.
题组二 向量在物理中的应用
4.(2022山东烟台第二中学期中)一条东西方向的河流两岸平行,河宽250 m,河水自西向东流,速度为3 km/h.一艘小货船准备从河南岸的码头P处出发,航行到河对岸的Q(PQ与河流的方向垂直)的正西方向并且与Q相距250 m的码头M处卸货,若水流的速度与小货船航行的速度的合速度的大小为5 km/h,则当小货船的航程最短时,小货船航行速度的大小为( )
A.3 km/h B.6 km/h
C.7 km/h D.3 km/h
5.当两人同提重|G|的书包时,用力大小都为|F|,两力的夹角为θ,且|F|,|G|,θ之间的关系为|F|=.当θ= 时,|F|取得最小值;当|F|=|G|时,θ= .
6.如图,在同一平面内,一个质点O受三个力F1,F2,F3的作用保持平衡,其中F3与F2的夹角为α,F3与F1的夹角为β.
(1)若α=120°,β=150°,|F3|=10,求力F1,F2的大小;
(2)若|F1|∶|F2|∶|F3|=1∶,求α与β的余弦值.
答案与分层梯度式解析
第二章 平面向量及其应用
6.2 平面向量在几何、物理中的应用举例
基础过关练
3.C 4.A 5.BD
1.证明 设=x,=y,
则y+y+(x-y)=(2x+y),
y+x=(2x+y),
∴,又MC与MN有公共点M,
∴M,N,C三点共线.
2.证明 由已知得=(4,-2),故,
又=(3,6)不为零向量,且不与平行,所以以A,B,C,D为顶点的四边形是平行四边形.又=4×3-2×6=0,所以,故以A,B,C,D为顶点的四边形是一个矩形.
3.C 设每根绳子拉力的大小为T N,礼物降落伞的总质量为m,
根据平衡条件可得,8T·cos 30°=mg,
解得T=≈16.97,
所以降落伞在匀速下落的过程中每根绳子拉力的大小约为16.97 N.故选C.
4.A 如图,设||=7,
合力的大小即为||=8,
将两边平方可得(,
即||2,
∴62+2×6×7×cos θ+72=82,解得cos θ=-.
5.BD 设船的实际航行速度为v1,水流速度为v2,船的航行速度为v3,
根据题意得|v3|= km/h,
设船的航行方向和水流方向的夹角为θ,90°<θ<180°,
则tan(180°-θ)=,
所以θ=120°,故选BD.
6.解析 设A,B处所受绳子的拉力分别为f1,f2,10 N的重力用f表示,则f1+f2=f.
如图,以重力作用点C为f1,f2的始点,作平行四边形CEWF,使CW为对角线,则=f1,=f2,=f,则∠FCW=180°-150°=30°,∠ECW=180°-120°=60°,
∴∠FCE=90°,∴四边形CEWF为矩形.
∴|f1|=||cos 30°=10×,
|f2|=||cos 60°=10×=5,
即A处受绳子拉力的大小为5 N,B处受绳子拉力的大小为5 N.
能力提升练
1.证明 设=a,=b,
则a,=b+a.
∵共线,
∴存在实数λ,使,
∴-b=a+(λ-1)b.
∵共线,
∴存在实数μ,使)=μ(a-b).
于是a+(λ-1)b=μ(a-b),
即a=(1-λ-μ)b.
∵a与b不共线,
∴
∴,即BE=BA.
2.证明 设=a,=b,=c,=d,=e,
则a=e+c,b=e+d,
所以a2-b2=(e+c)2-(e+d)2=c2+2e·c-2e·d-d2,
由题意得a2-b2=c2-d2,
所以e·c-e·d=0,即e·(c-d)=0,
即=0,所以,
所以AD⊥BC.
3.解析 (1)如图,建立平面直角坐标系,
则D(2,3),E(1,0),设P(0,y),0≤y≤3,
则=(-1,y),
∴|=3y-1,
∴cos 45°=,
解得y=2(负值舍去),
∴点P为线段AB上靠近点A的三等分点时,∠PED=45°.
(2)证明:连接DP,由(1)知当∠PED=45°时,P(0,2),
则=(-1,2),
∴=0,∴∠DPE=90°,
又∠DCE=90°,∴D,P,E,C四点在以DE为直径的圆上,即D,P,E,C四点共圆.
4.C 由题意知,当小货船的航程最短时,航线为线段PM,设小货船航行速度为v,水流的速度为v1,水流速度与小货船航行速度的合速度为v2,作出示意图如下:
由题知,PQ=250 m,QM=250 m,在Rt△PQM中,tan∠PMQ=,所以∠PMQ=,
所以∠MPQ=,
又v=v2-v1,
所以|v|==7,
所以小货船航行速度的大小为7 km/h,故选C.
5.答案 0;
解析 因为|F| =,
所以当cos =1,即θ=0时,|F|取得最小值.
当|F|=|G|时,cos ,此时θ=.
6.解析 (1)因为质点在F1,F2,F3的作用下保持平衡,所以F1+F2+F3=0,所以F3=-(F1+F2),
又α=120°,β=150°,
所以F1与F2的夹角为90°,所以F1·F2=0,
则|F3|2=[-(F1+F2)]2=+2F1·F2+,
将|F3|=10代入可得=100.
如图.
易得∠1=30°, 所以|F1|=|F3|×cos 30°=10×,
|F2|=|F3|×sin 30°=10×=5.
(2)因为|F1|∶|F2|∶|F3|=1∶,且质点处于平衡状态,
所以以|F1|,|F2|,|F3|为边长的三角形为直角三角形,如图所示,
则cos∠3=,cos∠2=,
所以cos β=cos(π-∠3)=-cos∠3=-,
cos α=cos(π-∠2)=-cos∠2=-.
方法总结 用数学知识解决物理问题时,首先要把物理问题转化为数学问题,也就是将物理量之间的关系抽象成数学模型,然后通过对这个数学模型的研究解释相关的物理现象.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
