7.1.2 平面直角坐标系
文档属性
| 名称 | 7.1.2 平面直角坐标系 |
|
|
| 格式 | zip | ||
| 文件大小 | 252.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-22 00:00:00 | ||
图片预览

文档简介
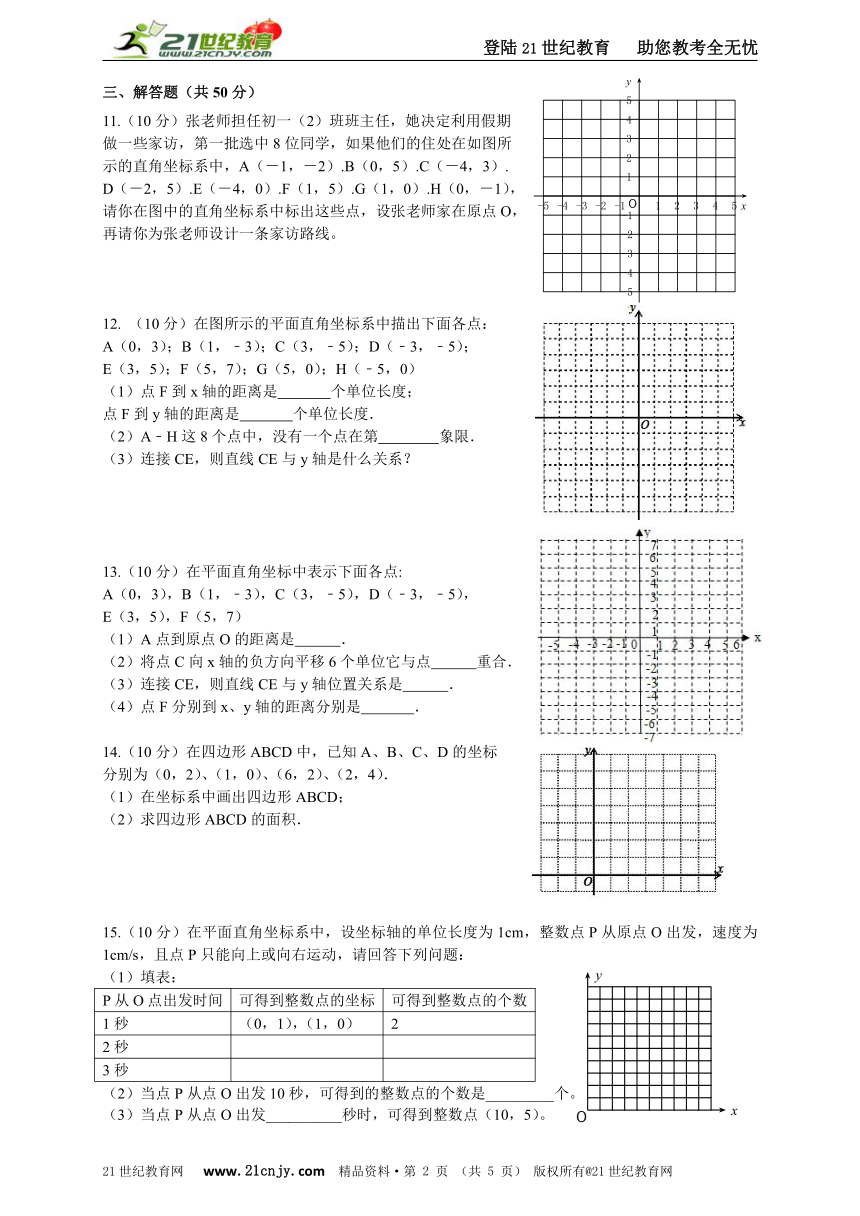
八年级数学(下)课时卷
7.1.2平面直角坐标系
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.点A(-2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图所示,在平面直角坐标系中,坐标是(0,-3)的点是( )
A.点A B.点B C.点C D.点D
第2题图 第3题图 第5题图
3.如图所示,小明用手盖住的点的坐标可能为( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
4.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标可能是( )
A.(1,2) B.(-1,-2) C.(1,-2) D.(-2,1)
5.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )21cnjy.com
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
二、填空题(每题5分,共25分)
6.如图所示,△ABC三个顶点的坐标分别是A(____,____)、B(____,____)、C(____,____).
第6题图 第8题图
7.如果点P在第二象限内,点P到轴的距离是4,到轴的距离是3,那么点P的坐标为 .
8.如图所示,是象棋棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4, -1)上,则“炮”所在的点的坐标是___________ .21·cn·jy·com
9.在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .2·1·c·n·j·y
10.在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,则端点B的坐标是 .【来源:21·世纪·教育·网】
三、解答题(共50分)
11.(10分)张老师担任初一(2)班班主任,她决定利用假期
做一些家访,第一批选中8位同学,如果他们的住处在如图所
示的直角坐标系中,A(-1,-2).B(0,5).C(-4,3).
D(-2,5).E(-4,0).F(1,5).G(1,0).H(0,-1),
请你在图中的直角坐标系中标出这些点,设张老师家在原点O,
再请你为张老师设计一条家访路线。
12. (10分)在图所示的平面直角坐标系中描出下面各点:
A(0,3);B(1,﹣3);C(3,﹣5);D(﹣3,﹣5);
E(3,5);F(5,7);G(5,0);H(﹣5,0)
(1)点F到x轴的距离是 个单位长度;
点F到y轴的距离是 个单位长度.
(2)A﹣H这8个点中,没有一个点在第 象限.
(3)连接CE,则直线CE与y轴是什么关系?
13.(10分)在平面直角坐标中表示下面各点:
A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),
E(3,5),F(5,7)
(1)A点到原点O的距离是 .
(2)将点C向x轴的负方向平移6个单位它与点 重合.
(3)连接CE,则直线CE与y轴位置关系是 .
(4)点F分别到x、y轴的距离分别是 .
14.(10分)在四边形ABCD中,已知A、B、C、D的坐标
分别为(0,2)、(1,0)、(6,2)、(2,4).
(1)在坐标系中画出四边形ABCD;
(2)求四边形ABCD的面积.
15.(10分)在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:21世纪教育网版权所有
(1)填表:
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1),(1,0)
2
2秒
3秒
(2)当点P从点O出发10秒,可得到的整数点的个数是_________个。
(3)当点P从点O出发__________秒时,可得到整数点(10,5)。
参考答案
7.1.2平面直角坐标系
【解析】∵点M到x轴的距离为1,到y轴的距离为2,∴点M的横坐标为2或-2,纵坐标是1或-1,∴点M的坐标为(2,1)或(2,-1)或(-2,1)或(-2,-1).故选D.
5.A
【解析】3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);63秒到了(7,0);∴那么第63秒后质点所在位置的坐标是(7,0).21教育网
6.-2,3;2,0;-1,-1
【解析】根据平面直角坐标系写出点的坐标即可.
7.(-3,4).
【解析】∵点P到x轴的距离是4,到y轴的距离是3,∴点P的纵坐标是4,横坐标是3.
又∵点P位于第二象限,∴P(﹣3,4).故答案是:(﹣3,4).
8.(-1,2)
【解析】∵帅位于点(2,-1)上,相位于点(4,-1)上,∴帅、相的横坐标分别为2,4,所以y轴在帅的左侧第2条竖线上,再根据纵坐标都为-1,可知x轴在这两点上方第1条线上,∴原点如图所示,∴炮的坐标为(-1,2).故答案为:(-1,2)www.21-cn-jy.com
9.(9,81).
【解析】首先观察各点坐标,找出一般规律,然后根据规律确定点A9的坐标.
10.(﹣5,4)或(3,4)
【解析】∵线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,
∴点B可能在A点右侧或左侧,
则端点B的坐标是:(﹣5,4)或(3,4).
故答案为:(﹣5,4)或(3,4).
11.答案见解析
【解析】
描出各点,如下图所示。设计家访路线时,以路程较短为原则,如:O→G→H→A→E→C→D→B→F。
13. (1)3;(2)D;(3)平行;(4)7,5.
【解析】如图所示(1)A点到原点O的距离是3﹣0=3.
(2)将点C向x轴的负方向平移6个单位它与点D重合.
(3)连接CE,则直线CE与y轴位置关系是平行.
(4)点F分别到x、y轴的距离分别是7,5.
故答案为:3;D;平行;7,5.
14.(1)如图所示.
(2)根据图示知( )
S△ABC+S△ADC=S四边形ABCD,
∵S△ABC=AC?BE=×6×2=6,
S△ADC=AC?DF=×6×2=6;
∴S四边形ABCD=6+6=12.
7.1.2平面直角坐标系
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.点A(-2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图所示,在平面直角坐标系中,坐标是(0,-3)的点是( )
A.点A B.点B C.点C D.点D
第2题图 第3题图 第5题图
3.如图所示,小明用手盖住的点的坐标可能为( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
4.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标可能是( )
A.(1,2) B.(-1,-2) C.(1,-2) D.(-2,1)
5.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )21cnjy.com
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
二、填空题(每题5分,共25分)
6.如图所示,△ABC三个顶点的坐标分别是A(____,____)、B(____,____)、C(____,____).
第6题图 第8题图
7.如果点P在第二象限内,点P到轴的距离是4,到轴的距离是3,那么点P的坐标为 .
8.如图所示,是象棋棋盘的一部分,若“帅”位于点(2,-1)上,“相”位于点(4, -1)上,则“炮”所在的点的坐标是___________ .21·cn·jy·com
9.在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .2·1·c·n·j·y
10.在平面直角坐标系中,已知线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,则端点B的坐标是 .【来源:21·世纪·教育·网】
三、解答题(共50分)
11.(10分)张老师担任初一(2)班班主任,她决定利用假期
做一些家访,第一批选中8位同学,如果他们的住处在如图所
示的直角坐标系中,A(-1,-2).B(0,5).C(-4,3).
D(-2,5).E(-4,0).F(1,5).G(1,0).H(0,-1),
请你在图中的直角坐标系中标出这些点,设张老师家在原点O,
再请你为张老师设计一条家访路线。
12. (10分)在图所示的平面直角坐标系中描出下面各点:
A(0,3);B(1,﹣3);C(3,﹣5);D(﹣3,﹣5);
E(3,5);F(5,7);G(5,0);H(﹣5,0)
(1)点F到x轴的距离是 个单位长度;
点F到y轴的距离是 个单位长度.
(2)A﹣H这8个点中,没有一个点在第 象限.
(3)连接CE,则直线CE与y轴是什么关系?
13.(10分)在平面直角坐标中表示下面各点:
A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),
E(3,5),F(5,7)
(1)A点到原点O的距离是 .
(2)将点C向x轴的负方向平移6个单位它与点 重合.
(3)连接CE,则直线CE与y轴位置关系是 .
(4)点F分别到x、y轴的距离分别是 .
14.(10分)在四边形ABCD中,已知A、B、C、D的坐标
分别为(0,2)、(1,0)、(6,2)、(2,4).
(1)在坐标系中画出四边形ABCD;
(2)求四边形ABCD的面积.
15.(10分)在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:21世纪教育网版权所有
(1)填表:
P从O点出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
(0,1),(1,0)
2
2秒
3秒
(2)当点P从点O出发10秒,可得到的整数点的个数是_________个。
(3)当点P从点O出发__________秒时,可得到整数点(10,5)。
参考答案
7.1.2平面直角坐标系
【解析】∵点M到x轴的距离为1,到y轴的距离为2,∴点M的横坐标为2或-2,纵坐标是1或-1,∴点M的坐标为(2,1)或(2,-1)或(-2,1)或(-2,-1).故选D.
5.A
【解析】3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);63秒到了(7,0);∴那么第63秒后质点所在位置的坐标是(7,0).21教育网
6.-2,3;2,0;-1,-1
【解析】根据平面直角坐标系写出点的坐标即可.
7.(-3,4).
【解析】∵点P到x轴的距离是4,到y轴的距离是3,∴点P的纵坐标是4,横坐标是3.
又∵点P位于第二象限,∴P(﹣3,4).故答案是:(﹣3,4).
8.(-1,2)
【解析】∵帅位于点(2,-1)上,相位于点(4,-1)上,∴帅、相的横坐标分别为2,4,所以y轴在帅的左侧第2条竖线上,再根据纵坐标都为-1,可知x轴在这两点上方第1条线上,∴原点如图所示,∴炮的坐标为(-1,2).故答案为:(-1,2)www.21-cn-jy.com
9.(9,81).
【解析】首先观察各点坐标,找出一般规律,然后根据规律确定点A9的坐标.
10.(﹣5,4)或(3,4)
【解析】∵线段AB∥x轴,端点A的坐标是(﹣1,4)且AB=4,
∴点B可能在A点右侧或左侧,
则端点B的坐标是:(﹣5,4)或(3,4).
故答案为:(﹣5,4)或(3,4).
11.答案见解析
【解析】
描出各点,如下图所示。设计家访路线时,以路程较短为原则,如:O→G→H→A→E→C→D→B→F。
13. (1)3;(2)D;(3)平行;(4)7,5.
【解析】如图所示(1)A点到原点O的距离是3﹣0=3.
(2)将点C向x轴的负方向平移6个单位它与点D重合.
(3)连接CE,则直线CE与y轴位置关系是平行.
(4)点F分别到x、y轴的距离分别是7,5.
故答案为:3;D;平行;7,5.
14.(1)如图所示.
(2)根据图示知( )
S△ABC+S△ADC=S四边形ABCD,
∵S△ABC=AC?BE=×6×2=6,
S△ADC=AC?DF=×6×2=6;
∴S四边形ABCD=6+6=12.
