第五单元第4课时组合图形面积的计算课件(共32张PPT)2023-2024学年五年级上册数学同步备课(青岛版)
文档属性
| 名称 | 第五单元第4课时组合图形面积的计算课件(共32张PPT)2023-2024学年五年级上册数学同步备课(青岛版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 07:06:54 | ||
图片预览










文档简介
(共32张PPT)
5.4合作探索:组合图形面积的计算
青岛版五年级数学上册素养达标课件
核心素养
结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
通过找一找、分一分、拼一拼,培养识图的能力和综合运用有关知识的能力,能合理地运用“割”“补”等方法来计算组合图形的面积。
培养合作、探索意识以及创新精神,养成积极参与数学学习活动的好习惯。
01
02
03
探索并掌握组合图形的面积计算方法。
理解并掌握组合图形的组合及分解方法。
能运用所学知识,解决生活中组合图形的实际问题。
课时目标
知识链接,感受文化素养。
学习任务一
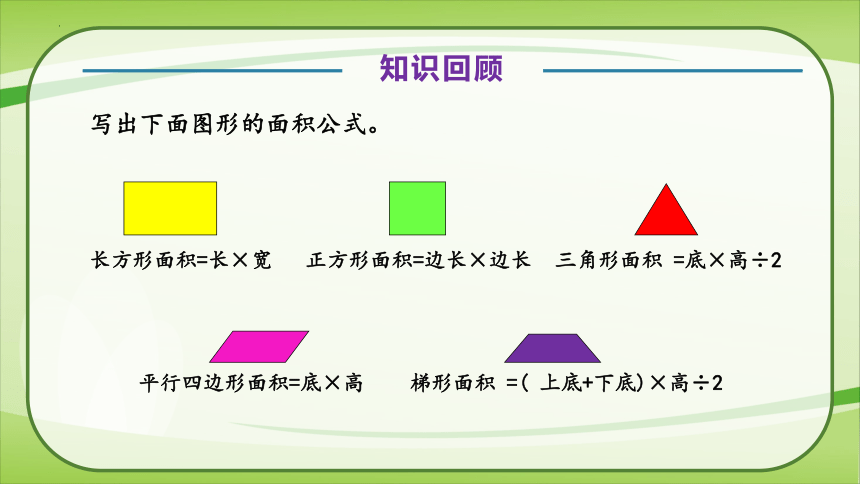
知识回顾
写出下面图形的面积公式。
长方形面积=长×宽
正方形面积=边长×边长
三角形面积 =底×高÷2
平行四边形面积=底×高
梯形面积 =( 上底+下底)×高÷2
知识链接
4
你能提出什么问题?
知识链接
虾池的面积是多少平方米?
虾池示意图
由多个基本图形组成的图形叫作组合图形。
知识链接
它是由一个梯形和一个长方形组成的,面积是......
40×80=3200(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
80米
30米
40米
90米
虾池示意图
=110×50÷2
梯形的面积:
(30+80)×(90-40)÷2
=2750(平方米)
长方形的面积:
组合图形的面积:
2750+3200=5950(平方米)
分割法一
知识链接
还可以分割成什么图形?
分割法二
80 米
30 米
40 米
90 米
虾池示意图
90×30=2700(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
=130×(80-30)÷2
梯形的面积:
(40+90)×(80-30)÷2
=3250(平方米)
长方形的面积:
组合图形的面积:
3250+2700=5950(平方米)
知识链接
分割法三
40×80=3200(平方米)
答:这个虾池的面积是5950平方米。
=30×50
长方形的面积:
30×(90-40)
=1500(平方米)
长方形的面积:
组合图形的面积:
1250+1500+3200=5950(平方米)
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
知识链接
分割法四
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
长方形的面积:
长方形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
30×90=2700(平方米)
40×(80-30)=2000(平方米)
组合图形的面积:
1250+2700+2000=5950(平方米)
答:这个虾池的面积是5950平方米。
知识链接
左上角补上一个三角形可以组成一个长方形......
S组合图形=S长方形 - S三角形
80 米
30 米
40 米
90 米
虾池示意图
90×80=7200(平方米)
答:这个虾池的面积是5950平方米。
长方形的面积:
组合图形的面积:
7200-1250=5950(平方米)
三角形的面积:
(90-40)×(80-30)÷2
=50×50÷2
=1250(平方米)
添补法
学习任务二
新知构建,完善核心素养。
学习活动
S组合图形 = S平行四边形+ S长方形
= 480(平方厘米)
15×12 - 5×5
S组合图形 = S长方形-S正方形
= 155(平方分米)
= 180 - 25
添补法
分割法
30×6 +30×10
= 180 +300
你会求下面图形的面积吗?
学习活动
S组合图形 = S梯形 + S三角形
(24+36)×8÷2 + 36×30÷2
= 780(cm2)
= 60×8÷2 + 1080÷2
= 240 + 540
分割法
计算组合图形的面积,要看清图形组合的特点,再确定用哪种方法计算。如果有多种解法时,要善于多中选优,选择最简便的方法。
学习活动
分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
学习任务三
学以致用,检验目标达成。
学习活动
1. 求下面图形的面积。
S组合图形 = S长方形-S三角形
8×12-8×7÷2=68(dm2)
S组合图形 = S正方形 + S梯形
8×8+(8+12)×4÷2=104(cm2)
学习活动
2.有一块五边形的沙发巾(如右图),制作这样一个沙发巾需要多少平方厘米的布料?
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料。
学习活动
3. 求下面图形的面积。
S组合图形 = S长方形 + 2×S正方形
6×3+2×2×2=26(cm2)
S组合图形 = S梯形 + 2×S三角形
(7+10)×8÷2+2×5×10÷2=118(cm2)
学习活动
4. 学校举办歌咏比赛,要制作一些锦旗(样式如右图)。做12面锦旗需要多少平方厘米布?
S组合图形 = S长方形 - S三角形
12×(60×30-30×15÷2)= 18900(cm2)
答:需要 18900 平方厘米的布。
学习活动
5. 下面图形的面积各是多少?(单位:cm)。
S组合图形 = S长方形 - S长方形
26×36-16×26=520(cm2)
S组合图形 = S正方形 -2× S三角形
30×30-2×10×12÷2=780(cm2)
学习活动
6.草坪占地多少平方米?
S组合图形 = S梯形 - S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
学习活动
7.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平方米需要用0.5千克涂料。如果涂料的价钱是每千克10 元,粉刷这面墙需要多少钱?
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
学习总结
今天你学会了什么?
你是怎么学会的?
素养评价
自我评价
内容 评价等级 A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级 A B C
学习态度
学习自信
学习合作
5.4合作探索:组合图形面积的计算
青岛版五年级数学上册素养达标课件
核心素养
结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
通过找一找、分一分、拼一拼,培养识图的能力和综合运用有关知识的能力,能合理地运用“割”“补”等方法来计算组合图形的面积。
培养合作、探索意识以及创新精神,养成积极参与数学学习活动的好习惯。
01
02
03
探索并掌握组合图形的面积计算方法。
理解并掌握组合图形的组合及分解方法。
能运用所学知识,解决生活中组合图形的实际问题。
课时目标
知识链接,感受文化素养。
学习任务一
知识回顾
写出下面图形的面积公式。
长方形面积=长×宽
正方形面积=边长×边长
三角形面积 =底×高÷2
平行四边形面积=底×高
梯形面积 =( 上底+下底)×高÷2
知识链接
4
你能提出什么问题?
知识链接
虾池的面积是多少平方米?
虾池示意图
由多个基本图形组成的图形叫作组合图形。
知识链接
它是由一个梯形和一个长方形组成的,面积是......
40×80=3200(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
80米
30米
40米
90米
虾池示意图
=110×50÷2
梯形的面积:
(30+80)×(90-40)÷2
=2750(平方米)
长方形的面积:
组合图形的面积:
2750+3200=5950(平方米)
分割法一
知识链接
还可以分割成什么图形?
分割法二
80 米
30 米
40 米
90 米
虾池示意图
90×30=2700(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
=130×(80-30)÷2
梯形的面积:
(40+90)×(80-30)÷2
=3250(平方米)
长方形的面积:
组合图形的面积:
3250+2700=5950(平方米)
知识链接
分割法三
40×80=3200(平方米)
答:这个虾池的面积是5950平方米。
=30×50
长方形的面积:
30×(90-40)
=1500(平方米)
长方形的面积:
组合图形的面积:
1250+1500+3200=5950(平方米)
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
知识链接
分割法四
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
长方形的面积:
长方形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
30×90=2700(平方米)
40×(80-30)=2000(平方米)
组合图形的面积:
1250+2700+2000=5950(平方米)
答:这个虾池的面积是5950平方米。
知识链接
左上角补上一个三角形可以组成一个长方形......
S组合图形=S长方形 - S三角形
80 米
30 米
40 米
90 米
虾池示意图
90×80=7200(平方米)
答:这个虾池的面积是5950平方米。
长方形的面积:
组合图形的面积:
7200-1250=5950(平方米)
三角形的面积:
(90-40)×(80-30)÷2
=50×50÷2
=1250(平方米)
添补法
学习任务二
新知构建,完善核心素养。
学习活动
S组合图形 = S平行四边形+ S长方形
= 480(平方厘米)
15×12 - 5×5
S组合图形 = S长方形-S正方形
= 155(平方分米)
= 180 - 25
添补法
分割法
30×6 +30×10
= 180 +300
你会求下面图形的面积吗?
学习活动
S组合图形 = S梯形 + S三角形
(24+36)×8÷2 + 36×30÷2
= 780(cm2)
= 60×8÷2 + 1080÷2
= 240 + 540
分割法
计算组合图形的面积,要看清图形组合的特点,再确定用哪种方法计算。如果有多种解法时,要善于多中选优,选择最简便的方法。
学习活动
分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
学习任务三
学以致用,检验目标达成。
学习活动
1. 求下面图形的面积。
S组合图形 = S长方形-S三角形
8×12-8×7÷2=68(dm2)
S组合图形 = S正方形 + S梯形
8×8+(8+12)×4÷2=104(cm2)
学习活动
2.有一块五边形的沙发巾(如右图),制作这样一个沙发巾需要多少平方厘米的布料?
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料。
学习活动
3. 求下面图形的面积。
S组合图形 = S长方形 + 2×S正方形
6×3+2×2×2=26(cm2)
S组合图形 = S梯形 + 2×S三角形
(7+10)×8÷2+2×5×10÷2=118(cm2)
学习活动
4. 学校举办歌咏比赛,要制作一些锦旗(样式如右图)。做12面锦旗需要多少平方厘米布?
S组合图形 = S长方形 - S三角形
12×(60×30-30×15÷2)= 18900(cm2)
答:需要 18900 平方厘米的布。
学习活动
5. 下面图形的面积各是多少?(单位:cm)。
S组合图形 = S长方形 - S长方形
26×36-16×26=520(cm2)
S组合图形 = S正方形 -2× S三角形
30×30-2×10×12÷2=780(cm2)
学习活动
6.草坪占地多少平方米?
S组合图形 = S梯形 - S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
学习活动
7.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平方米需要用0.5千克涂料。如果涂料的价钱是每千克10 元,粉刷这面墙需要多少钱?
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
学习总结
今天你学会了什么?
你是怎么学会的?
素养评价
自我评价
内容 评价等级 A B C
学习态度
学习自信
学习合作
小组互评
内容 评价等级 A B C
学习态度
学习自信
学习合作
