陕西2008年中考数学备考策略--数与代数
文档属性
| 名称 | 陕西2008年中考数学备考策略--数与代数 |  | |
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-04 21:16:00 | ||
图片预览






文档简介
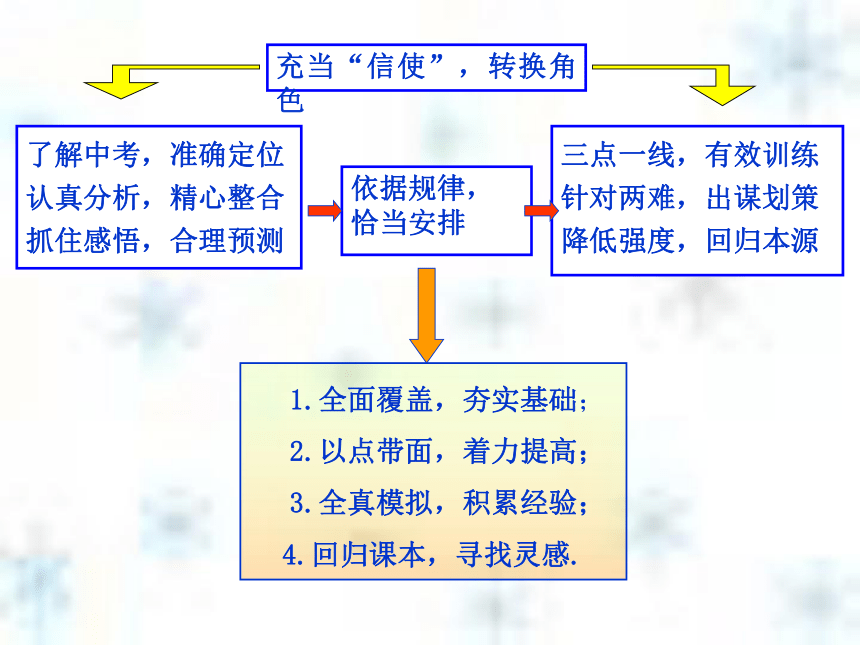
课件44张PPT。2008中考备考建议西安铁一中学王丽莉数与代数了解中考,准确定位
认真分析,精心整合
抓住感悟,合理预测
依据规律,
恰当安排三点一线,有效训练
针对两难,出谋划策
降低强度,回归本源 充当“信使”,转换角色 1.全面覆盖,夯实基础;
2.以点带面,着力提高;
3.全真模拟,积累经验;
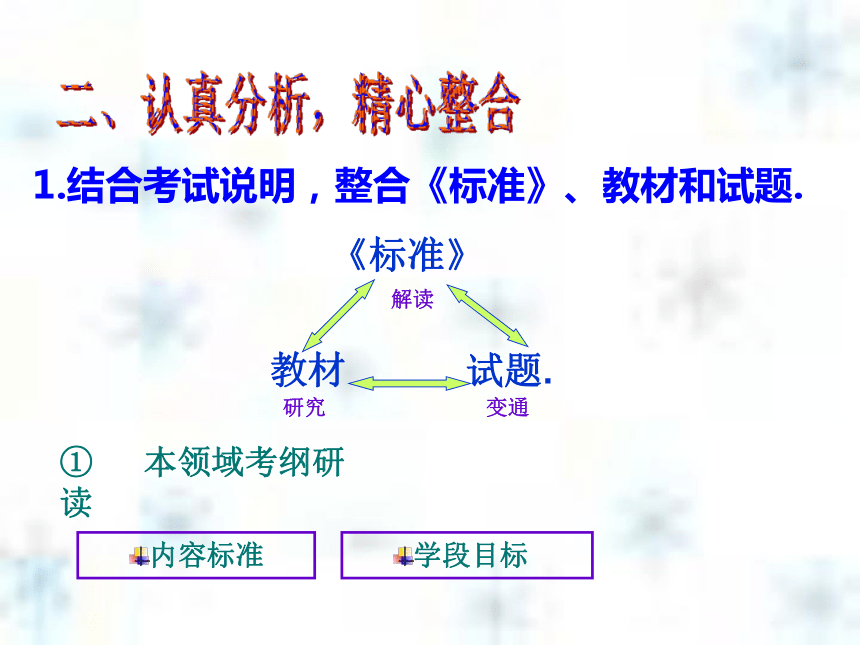
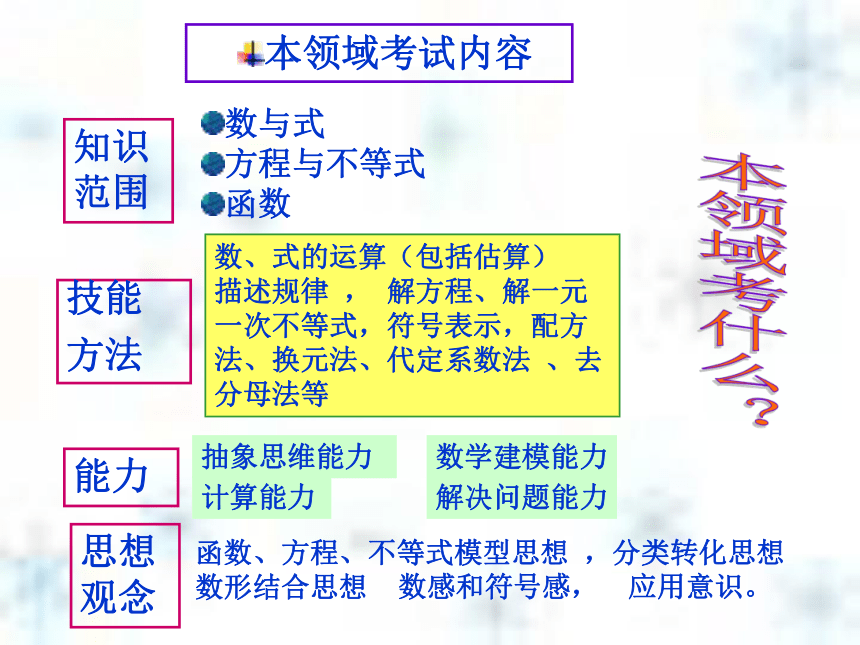
4.回归课本,寻找灵感.一、了解中考,准确定位1. 考试性质 2.命题依据3.准确定位两试兼容毕业升学依标靠本二、认真分析,精心整合结合考试说明,整合《标准》、教材和试题.《标准》教材试题.解读 研究 变通 本领域考纲研读 内容标准学段目标本领域考什么?本领域考试内容② 本领域内容教材呈现特点知识零碎分散
分段达标
螺旋上升
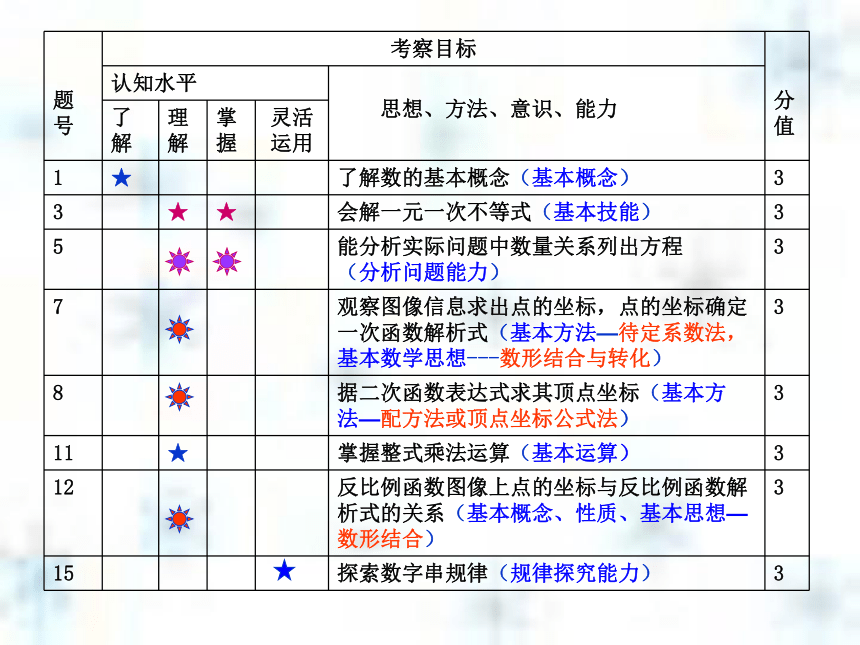
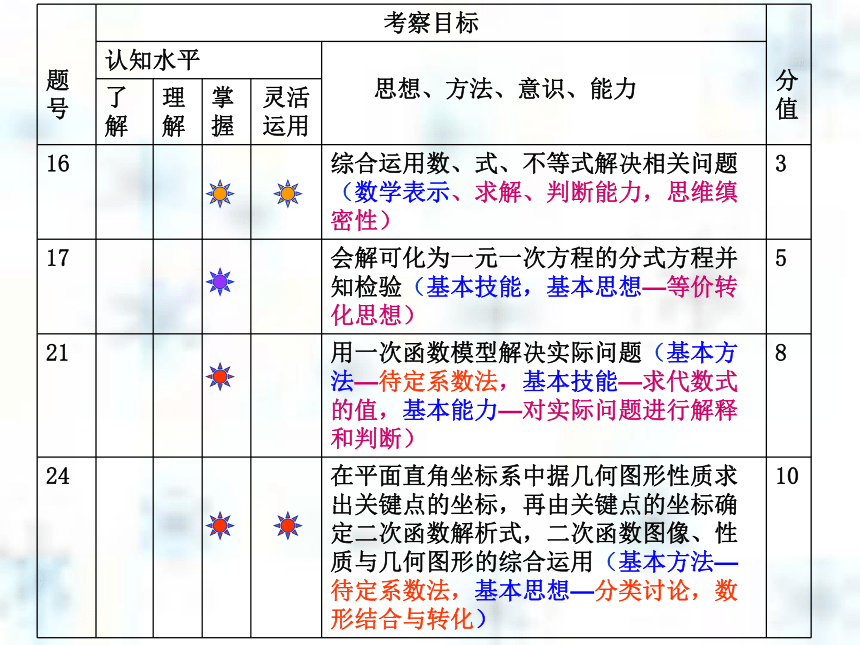
内容展开模式:问题情景—建立模型—解释、应用与拓展③我省07年本领域中考试题特点07我省中考中对“数与代数”领域的考察情况分值比例: 在分值上本对领域内容的考察约占全卷的42%,与07年考试说明基本吻合, “数与式”、“方程与不等式”、 “函数”所占分值比为8﹕11﹕22,呈逐步递增趋势;另有3分的探索数字串规律的试题.
考察目标:在考试要求的难度分布上,从“数与式”到“方程与不等式”再到“函数”也呈递增趋势;考察了基础知识、基本技能,基本方法、基本数学思想,淡化了特殊技巧,注重再对核心知识和核心技能的考察中;考察通性、通法(三次考到用待定系数法确定函数解析式); 考察方式:在现实、有趣的问题情境中,以本学段数与代数领域的知识技能目标为基础,考察学生对基础知识和基本技能、基本数学思想方法的理解和掌握程度;
试题立意:命题以数学思想和能力立意,体现了对学生综合运用能力和创新精神的考察.
怎么考?立足考察四基,着重考察能力;试题背景现实、新颖、有趣;关注核心内容,体现创新精神2.在专家组、教研组和备课组之间进行资源整合成立备考领导小组潜心研究,科学组织,统一规划,有序实施
扎实展开工作.三、抓住感悟,合理预测继续关注核心内容中通性、通法的考察2.继续体现对学生数学应用能力的考查?3.关注归纳与表示立足考察基础,着眼考察能力,
加强综合应用,关注变化发展.①在探索并表示规律的过程中,归纳起着重要的作用② 利用一个恰当的模型表示数量关系或变化规律4.试题将更加注重数学思想立意5.更加关注对学生活动过程的考察四、依据规律,恰当安排(一)全面覆盖,夯实基础;
(二)以点带面,着力提高;
(三)全真模拟,积累经验;
(四)回归课本,寻找灵感.1. 本领域备考方案 2.本领域复习建议第一阶段复习建议注意三点①知识梳理应有“路”基础过关,紧扣考点 用框图整理“函数”的内容: 用树图归纳“方程”的内容:方程方程(组)、方程(组)的解、解方程(组)、解的检验.应用审----设----列----解---验---答概念:分类:一元方程二元方程(组)二次一次一次二次解法思想:消元、降次,化未知为已知 方法:代入消元、加减消元法,去分母 法,换元法,已知量所求量各量关系直接设元间接设元列代数式列方程②技能训练应有“度”③着重在概念的运用中理解概念,在明确算理的基础上,适当追求算法的多样化第二阶段复习建议三点一线,有效训练三点注重①注重本领域知识之间的综合 ②注重本领域与其他领域之间的综合 ③注重在不断反思、感悟的过程中培养能力第三阶段复习建议针对“两难”,出谋划策一条捷径①紧扣课表评价目录,结合学生情况,精心选编模拟试题②不断调整模拟试题区分度两处策划成题改编第四阶段复习建议降低强度,回归本源一点提醒:动态静息五、把握策略,转换角色,一个策略:“信使”谢谢! 再见! 本领域核心知识为函数,
本领域基本技能:数、式的运算,解方程(组)、不等式,确定函数解析式,构建简单的代数式、方程或函数模型,运用方程、不等式知识和函数基本性质解决实际问题.
本领域几个核心理念:
①数感;②符号感;⑤应用意识
主要的方法有:方程中的消元法、换元法、去分母法,配方法、公式法,
函数中的待定系数法等
主要的数学思想有:估算思想、整体思想、模型思想,数形结合思想,分类与转化思想等AAAAA4×3+1=4×4-34×4+1=4×5-34×(n-1)+1=4×n-307陕西第5题
中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金x元,则所列方程正确的是( )
A.
B.
C.
D.C例5. (本题满分8分)根据以下10个乘积,回答问题:
11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.
(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;
(2)将以上10个乘积按照从小到大的顺序排列起来;
(3)试由(1)、(2)猜测一个一般性的结论.(不要求证明) 11×29=202-92;12×28=202-82;13×27=202-72;…20×20=202-02. 例如,11×29;假设11×29=□2-○2,
因为□2-○2=(□+○)(□-○);
所以,可以令□-○=11,□+○=29.
解得,□=20,○=9.故(或11×29=(20-9)(20+9)=202-92 … ① 若,a,b是自然数,则ab≤202=400.
② 若a+b=40,则ab≤202=400.
③ 若a+b=m,a,b是自然数,则ab≤ .
④ 若a+b=m,则ab≤ .
⑤ 若a,b的和为定值,则ab的最大值为 .
⑥ 若a1+b1=a2+b2=a3+b3=…=an+bn=40.
且| a1-b1|≥|a2-b2|≥|a3-b3|≥…≥| an-bn|,
则 a1b1≤a2b2 ≤ a3b3 ≤…≤ anbn .
⑦ 若a1+b1=a2+b2=a3+b3=…=an+bn=m.
且| a1-b1|≥|a2-b2|≥|a3-b3|≥…≥| an-bn|,
则 a1b1≤a2b2 ≤ a3b3 ≤…≤ anbn .
⑧ 若a+b=m,a,b差的绝对值越大,则它们的积就越小. 例.根据以下10个乘积,回答问题:
11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.
(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;
(2)将以上10个乘积按照从小到大的顺序排列起来;
(3)试由(1)、(2)猜测一个一般性的结论.(不要求证明) 例8. 07武汉25题
25.如图①,在平面直角坐标系中,Rt△AOB≌Rt△CDA,且
A(-1,0)、B(0,2),抛物线y=ax2+ax-2经过点C.
(1)求抛物线的解析式;
(2)在抛物线(对称轴的右侧)上是否存在两点P、Q,使四边形ABPQ是正方形?若存在,求点P、Q的坐标,若不存在,请说明理由;
例1 .(2007年兰州市)
某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现在两种方案:①围成一个矩形(如下左图);②围成一个半圆形(如下右图).设矩形的面积为S1平方米,宽为x米,半圆形的面积为S2平方米,半径为x米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(π=3).??是 .本题呈现方式:采用“数字转换器”的形式,
其特点是:表述形象、简洁,富有趣味性,学生易懂
考察内容丰富.
①建立y与x的两个不同的关系式,
②再依据y>100得到两个不等式,并求出这两个不等式的最小正整数解;×4+3×5③关键是最后还要比较这两个不等式的最小正整数解,确定这两者间的最小值,
④考察了学生灵活运用数、式和不等式的有关知识解决问题的能力和等价转化能力.同时也考察了学生思维的缜密性.王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.例4.(2006年陕西省考题 回头看)25题 (1)求FC的长;图形运动中的函数关系利用数据的特殊性:
用简单的运算
考核基本知识(1)求FC的长;
(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x为多少时,矩形的面积y最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.命题特征第(2)问探求图形运动中两个变量间(面积与线段)的关系,并写出定义域;第(1)问先求一个关键量,为下面作好暗示和铺垫;第(3)问探求特殊性,一般用方程的思想。试题背景:以社会生产中常见的问题为背景,命题方式:以学生熟悉的图形裁剪为载体,将数学溶于操作之中,搭建探究的平台,考查内容:函数、方程、相似三角形等知识.以及考生在实际问题中运用数学思想和数学方法解决实际问题的能力.不同程度学生的思维品质 题目蕴含有从实际问题→几何模型→函数模型和方程模型的逐步数学化的过程,考生需要同时具备模型思想和分类意识,并且需要用心体察文字和图形信息,充分利用图形性质建立函数关系,灵活进行几何—函数—方程—实际问题之间的结合与转化.因此,本题对学生的阅读理解能力、数形结合能力、实践探究能力和分类讨论能力均有较高的要求,学生易产生对题意揣摸不透、解题过程不完整、甚至直接用直观猜测替换逻辑推理的错误.造成难度上升07年河北25题7.如图,一次函数图象经过点 ,且与正比例函数 的图象交于点 ,则该一次函数的表达式为( )15.小说《达芬奇密码》中的一个故事里出现了一串神密排列的数,将这串令人费解的数按从小到大的顺序排列为: ,则这列数的第8个数是 .21.(本题满分8分)
为了迎接暑期旅游,某旅行社推出了一种价格优惠方案:从现在开始,各条旅游线路的价格每人(元)是原来价格每人(元)的一次函数.现知道其中两条旅游线路原来旅游价格分别为每人2100元和2800元,而现在旅游的价格分别为每人1800元和2300元.
(1)求与的函数关系式(不要求写出x的取值范围);
(2)王老师想参加该旅行社原价格为5600元的一条线路的暑期旅游,请帮王老师算出这条线路的价格.07陕西24.(本题满分10分)
如图,在直角梯形 中,
(1)求 两点的坐标;
(2)若线段 上存在点 ,使,求过
三点的抛物线的表达式.例10.有一长为24m的篱笆,一面利用墙(墙的最大长度为10m)围成中间隔有一道篱笆的长方形花圃(如图),设花圃宽AB为xm,面积为Sm??
(1)求S与x的函数关系式,并确定x的取值范围
(2)若要围成面积为45m2的花圃,AB的长应为多少??
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,如果不能,请说明理由.?人教社老教材代数第三册P126第4题新教材北师版九年级下P74第6题 本题从提问方式上看属于决策型试题的一种,虽然背景不太复杂,但“墙的可用长度最大为10米”这一条件约束了x的取值,如果考虑不全面,会直接影响后面的求解,许多解题者易忽视这一点,故从实际问题中构建的函数模型,应关注自变量的取值范围,本例综合了矩形周长、面积、方程、二次函数、不等式组等知识,考生需运用图形性质建立函数模型,综合运用数学知识和方法找到答案,并检验解的合理性,对实际问题并作出评判.?
认真分析,精心整合
抓住感悟,合理预测
依据规律,
恰当安排三点一线,有效训练
针对两难,出谋划策
降低强度,回归本源 充当“信使”,转换角色 1.全面覆盖,夯实基础;
2.以点带面,着力提高;
3.全真模拟,积累经验;
4.回归课本,寻找灵感.一、了解中考,准确定位1. 考试性质 2.命题依据3.准确定位两试兼容毕业升学依标靠本二、认真分析,精心整合结合考试说明,整合《标准》、教材和试题.《标准》教材试题.解读 研究 变通 本领域考纲研读 内容标准学段目标本领域考什么?本领域考试内容② 本领域内容教材呈现特点知识零碎分散
分段达标
螺旋上升
内容展开模式:问题情景—建立模型—解释、应用与拓展③我省07年本领域中考试题特点07我省中考中对“数与代数”领域的考察情况分值比例: 在分值上本对领域内容的考察约占全卷的42%,与07年考试说明基本吻合, “数与式”、“方程与不等式”、 “函数”所占分值比为8﹕11﹕22,呈逐步递增趋势;另有3分的探索数字串规律的试题.
考察目标:在考试要求的难度分布上,从“数与式”到“方程与不等式”再到“函数”也呈递增趋势;考察了基础知识、基本技能,基本方法、基本数学思想,淡化了特殊技巧,注重再对核心知识和核心技能的考察中;考察通性、通法(三次考到用待定系数法确定函数解析式); 考察方式:在现实、有趣的问题情境中,以本学段数与代数领域的知识技能目标为基础,考察学生对基础知识和基本技能、基本数学思想方法的理解和掌握程度;
试题立意:命题以数学思想和能力立意,体现了对学生综合运用能力和创新精神的考察.
怎么考?立足考察四基,着重考察能力;试题背景现实、新颖、有趣;关注核心内容,体现创新精神2.在专家组、教研组和备课组之间进行资源整合成立备考领导小组潜心研究,科学组织,统一规划,有序实施
扎实展开工作.三、抓住感悟,合理预测继续关注核心内容中通性、通法的考察2.继续体现对学生数学应用能力的考查?3.关注归纳与表示立足考察基础,着眼考察能力,
加强综合应用,关注变化发展.①在探索并表示规律的过程中,归纳起着重要的作用② 利用一个恰当的模型表示数量关系或变化规律4.试题将更加注重数学思想立意5.更加关注对学生活动过程的考察四、依据规律,恰当安排(一)全面覆盖,夯实基础;
(二)以点带面,着力提高;
(三)全真模拟,积累经验;
(四)回归课本,寻找灵感.1. 本领域备考方案 2.本领域复习建议第一阶段复习建议注意三点①知识梳理应有“路”基础过关,紧扣考点 用框图整理“函数”的内容: 用树图归纳“方程”的内容:方程方程(组)、方程(组)的解、解方程(组)、解的检验.应用审----设----列----解---验---答概念:分类:一元方程二元方程(组)二次一次一次二次解法思想:消元、降次,化未知为已知 方法:代入消元、加减消元法,去分母 法,换元法,已知量所求量各量关系直接设元间接设元列代数式列方程②技能训练应有“度”③着重在概念的运用中理解概念,在明确算理的基础上,适当追求算法的多样化第二阶段复习建议三点一线,有效训练三点注重①注重本领域知识之间的综合 ②注重本领域与其他领域之间的综合 ③注重在不断反思、感悟的过程中培养能力第三阶段复习建议针对“两难”,出谋划策一条捷径①紧扣课表评价目录,结合学生情况,精心选编模拟试题②不断调整模拟试题区分度两处策划成题改编第四阶段复习建议降低强度,回归本源一点提醒:动态静息五、把握策略,转换角色,一个策略:“信使”谢谢! 再见! 本领域核心知识为函数,
本领域基本技能:数、式的运算,解方程(组)、不等式,确定函数解析式,构建简单的代数式、方程或函数模型,运用方程、不等式知识和函数基本性质解决实际问题.
本领域几个核心理念:
①数感;②符号感;⑤应用意识
主要的方法有:方程中的消元法、换元法、去分母法,配方法、公式法,
函数中的待定系数法等
主要的数学思想有:估算思想、整体思想、模型思想,数形结合思想,分类与转化思想等AAAAA4×3+1=4×4-34×4+1=4×5-34×(n-1)+1=4×n-307陕西第5题
中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金x元,则所列方程正确的是( )
A.
B.
C.
D.C例5. (本题满分8分)根据以下10个乘积,回答问题:
11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.
(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;
(2)将以上10个乘积按照从小到大的顺序排列起来;
(3)试由(1)、(2)猜测一个一般性的结论.(不要求证明) 11×29=202-92;12×28=202-82;13×27=202-72;…20×20=202-02. 例如,11×29;假设11×29=□2-○2,
因为□2-○2=(□+○)(□-○);
所以,可以令□-○=11,□+○=29.
解得,□=20,○=9.故(或11×29=(20-9)(20+9)=202-92 … ① 若,a,b是自然数,则ab≤202=400.
② 若a+b=40,则ab≤202=400.
③ 若a+b=m,a,b是自然数,则ab≤ .
④ 若a+b=m,则ab≤ .
⑤ 若a,b的和为定值,则ab的最大值为 .
⑥ 若a1+b1=a2+b2=a3+b3=…=an+bn=40.
且| a1-b1|≥|a2-b2|≥|a3-b3|≥…≥| an-bn|,
则 a1b1≤a2b2 ≤ a3b3 ≤…≤ anbn .
⑦ 若a1+b1=a2+b2=a3+b3=…=an+bn=m.
且| a1-b1|≥|a2-b2|≥|a3-b3|≥…≥| an-bn|,
则 a1b1≤a2b2 ≤ a3b3 ≤…≤ anbn .
⑧ 若a+b=m,a,b差的绝对值越大,则它们的积就越小. 例.根据以下10个乘积,回答问题:
11×29; 12×28; 13×27; 14×26; 15×25;16×24; 17×23; 18×22; 19×21; 20×20.
(1)试将以上各乘积分别写成一个“□2-○2”(两数平方差)的形式,并写出其中一个的思考过程;
(2)将以上10个乘积按照从小到大的顺序排列起来;
(3)试由(1)、(2)猜测一个一般性的结论.(不要求证明) 例8. 07武汉25题
25.如图①,在平面直角坐标系中,Rt△AOB≌Rt△CDA,且
A(-1,0)、B(0,2),抛物线y=ax2+ax-2经过点C.
(1)求抛物线的解析式;
(2)在抛物线(对称轴的右侧)上是否存在两点P、Q,使四边形ABPQ是正方形?若存在,求点P、Q的坐标,若不存在,请说明理由;
例1 .(2007年兰州市)
某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现在两种方案:①围成一个矩形(如下左图);②围成一个半圆形(如下右图).设矩形的面积为S1平方米,宽为x米,半圆形的面积为S2平方米,半径为x米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(π=3).??是 .本题呈现方式:采用“数字转换器”的形式,
其特点是:表述形象、简洁,富有趣味性,学生易懂
考察内容丰富.
①建立y与x的两个不同的关系式,
②再依据y>100得到两个不等式,并求出这两个不等式的最小正整数解;×4+3×5③关键是最后还要比较这两个不等式的最小正整数解,确定这两者间的最小值,
④考察了学生灵活运用数、式和不等式的有关知识解决问题的能力和等价转化能力.同时也考察了学生思维的缜密性.王师傅有两块板材边角料,其中一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①),王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②),由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.例4.(2006年陕西省考题 回头看)25题 (1)求FC的长;图形运动中的函数关系利用数据的特殊性:
用简单的运算
考核基本知识(1)求FC的长;
(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x为多少时,矩形的面积y最大?最大面积是多少?(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.命题特征第(2)问探求图形运动中两个变量间(面积与线段)的关系,并写出定义域;第(1)问先求一个关键量,为下面作好暗示和铺垫;第(3)问探求特殊性,一般用方程的思想。试题背景:以社会生产中常见的问题为背景,命题方式:以学生熟悉的图形裁剪为载体,将数学溶于操作之中,搭建探究的平台,考查内容:函数、方程、相似三角形等知识.以及考生在实际问题中运用数学思想和数学方法解决实际问题的能力.不同程度学生的思维品质 题目蕴含有从实际问题→几何模型→函数模型和方程模型的逐步数学化的过程,考生需要同时具备模型思想和分类意识,并且需要用心体察文字和图形信息,充分利用图形性质建立函数关系,灵活进行几何—函数—方程—实际问题之间的结合与转化.因此,本题对学生的阅读理解能力、数形结合能力、实践探究能力和分类讨论能力均有较高的要求,学生易产生对题意揣摸不透、解题过程不完整、甚至直接用直观猜测替换逻辑推理的错误.造成难度上升07年河北25题7.如图,一次函数图象经过点 ,且与正比例函数 的图象交于点 ,则该一次函数的表达式为( )15.小说《达芬奇密码》中的一个故事里出现了一串神密排列的数,将这串令人费解的数按从小到大的顺序排列为: ,则这列数的第8个数是 .21.(本题满分8分)
为了迎接暑期旅游,某旅行社推出了一种价格优惠方案:从现在开始,各条旅游线路的价格每人(元)是原来价格每人(元)的一次函数.现知道其中两条旅游线路原来旅游价格分别为每人2100元和2800元,而现在旅游的价格分别为每人1800元和2300元.
(1)求与的函数关系式(不要求写出x的取值范围);
(2)王老师想参加该旅行社原价格为5600元的一条线路的暑期旅游,请帮王老师算出这条线路的价格.07陕西24.(本题满分10分)
如图,在直角梯形 中,
(1)求 两点的坐标;
(2)若线段 上存在点 ,使,求过
三点的抛物线的表达式.例10.有一长为24m的篱笆,一面利用墙(墙的最大长度为10m)围成中间隔有一道篱笆的长方形花圃(如图),设花圃宽AB为xm,面积为Sm??
(1)求S与x的函数关系式,并确定x的取值范围
(2)若要围成面积为45m2的花圃,AB的长应为多少??
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,如果不能,请说明理由.?人教社老教材代数第三册P126第4题新教材北师版九年级下P74第6题 本题从提问方式上看属于决策型试题的一种,虽然背景不太复杂,但“墙的可用长度最大为10米”这一条件约束了x的取值,如果考虑不全面,会直接影响后面的求解,许多解题者易忽视这一点,故从实际问题中构建的函数模型,应关注自变量的取值范围,本例综合了矩形周长、面积、方程、二次函数、不等式组等知识,考生需运用图形性质建立函数模型,综合运用数学知识和方法找到答案,并检验解的合理性,对实际问题并作出评判.?
同课章节目录
