4.8 图形的位似 课件(共24张PPT)九年级数学上册(北师大版)
文档属性
| 名称 | 4.8 图形的位似 课件(共24张PPT)九年级数学上册(北师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 22:14:43 | ||
图片预览






文档简介
(共24张PPT)
第四章 图形的相似
4.8 图形的位似
学习目标
1)了解位似多边形的有关概念.
2)通过图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化规律.
重点
掌握位似图像的性质,会画位似图形.
难点
理解位似图形的坐标变换规律.
观察下面四组图形有哪些相似点?
下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O.
, ,,,,有什么关系?
如果两个相似多边形一组对应顶点P,P 所在的直线都过同一点O,且
OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
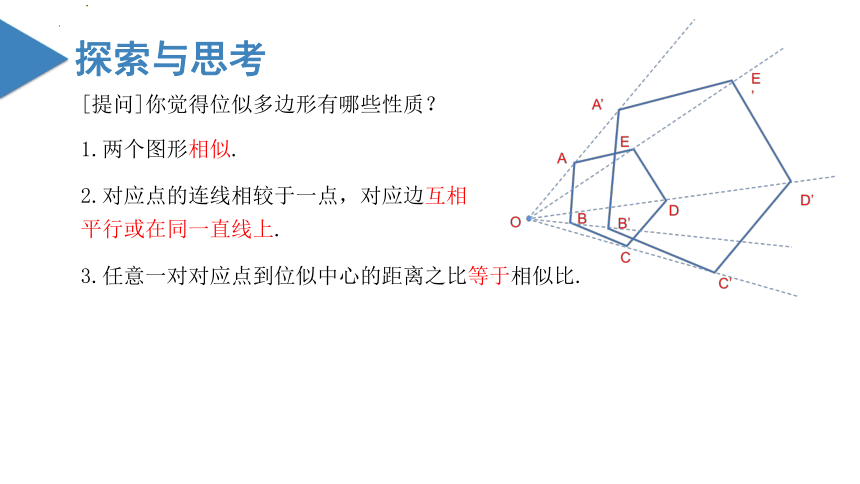
[提问]你觉得位似多边形有哪些性质?
1.两个图形相似.
2.对应点的连线相较于一点,对应边互相
平行或在同一直线上.
3.任意一对对应点到位似中心的距离之比等于相似比.
如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC上分别取点D,E,F,
使OD=2OA,OE=2OB,OF=2OC;
3)顺序连接D,E,F,则△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
你还有别的方法吗?
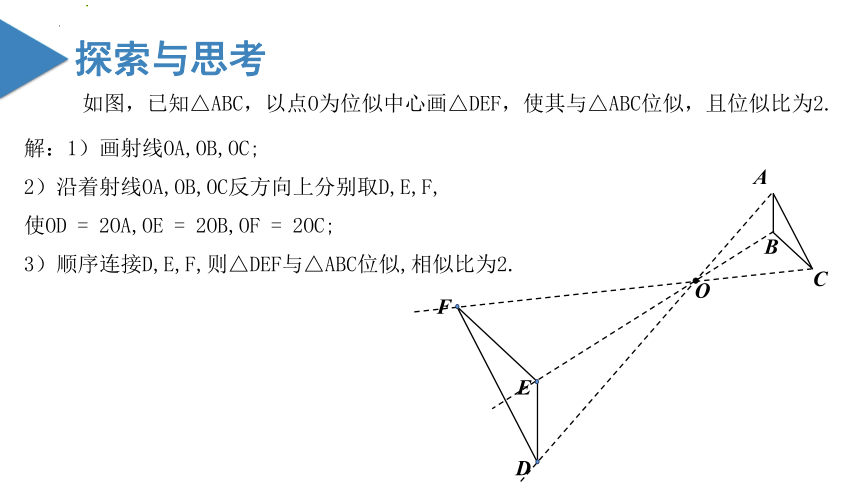
如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:1)画射线OA,OB,OC;
2)沿着射线OA,OB,OC反方向上分别取D,E,F,
使OD = 2OA,OE = 2OB,OF = 2OC;
3)顺序连接D,E,F,则△DEF与△ABC位似,相似比为2.
A
B
C
O
E
F
D
[提问]简述位似多边形的画法?
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
例1 已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法一:△ABC与△DEF在同侧
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC上分别取点D,E,F,
使OA = 2OD,OB = 2OE,OC = 2OF;
3)顺序连接D,E,F,则△DEF与△ABC位似,位似比为1:2.
D
E
F
例1 已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法二: △ABC与△DEF在异侧
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;
3)顺序连接D,E,F,则△DEF与△ABC位似,位似比为1:2.
D
F
E
1. 下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点到位似中心的距离之比等于相比.其中正确的序号是( )
A.② B.①② C.③④ D.②③④
【详解】③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,但没有对应边平行(或在同一条直线上),那么这两个图形不一定位似图形,此项错误;
2.下列各组图形中不是位似图形的是()
3.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
4.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0), A(3,0), B(2,3)
(1)将点O,A,B的横坐标、纵坐标都乘2,得到三个点,以这三个点位为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比.
x
y
O
2
4
-2
-4
2
4
A
B
A '
B '
6
位似,
位似中心为:原点O,
位似比为:1:2
在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0), A(3,0), B(2,3)
(2)将点O,A,B的横坐标、纵坐标都乘-2,得到三个点,以这三个点位为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比.
x
y
O
2
4
-2
-4
2
4
-2
-4
A
B
A '
B '
位似,
位似中心为:原点O,
位似比为:1:2
在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比位|k|.
例2 在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),
B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使它
与四边形OABC的相似是2:3.
画法一:如右图所示,
解:将四边形OABC各顶点的坐标都乘 ;
在平面直角坐标系中描点O(0,0), A'(4,0),B'(2,4)C'(-2, 2);
在平面直角坐标系中描点A',B',C',用线段顺次连接O,A',B',C'.
例2 在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),
B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使它
与四边形OABC的相似是2:3.
画法二:如右图所示,
解:将四边形OABC各顶点的坐标都乘-;
在平面直角坐标系中描点O(0,0), A''(-4,0),
B''(-2,-4),C''(-2,-2);
在平面直角坐标系中描点A'',B'',C'',用线段顺次连接O,A'',B'',C''.
1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2)当位似图形在原点同侧时,相似比为 k,与它对应的点的坐标为 (kx,ky) ;
当位似图形在原点两侧时,相似比为-k,与它对应的点的坐标为 (-kx,-ky) .
3)当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的k倍.
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【详解】根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以2或-2,
所以点E′的坐标为(8,-4)或(-8,4).故选B.
2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
3.如图,正方形OABC 与正方形ODEF是位似图,点O为位似中心,位似比为 2:3 ,点A的坐标为(0,2),则点E的坐标是 ____.
【详解】解:∵正方形OABC 与正方形ODEF是位似图,位似比为 2:3 ,
∴OA:OD=2:3,
∵点A 的坐标为(0,2),即OA=2,
∴OD=3,DE=EF=3,
故点E的坐标是(3,3).
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若DE=7.5,则AB=_____.
【详解】解:∵A(1.5,0),D(4.5,0)∴==,
∵△ABC与△DEF位似,原点O是位似中心,
∴==, ∴AB=DE=×7.5=2.5.
5.如图,△ ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点O为位似中心,画出一个三角形,使它与△ ABO的位似比为.
第四章 图形的相似
4.8 图形的位似
学习目标
1)了解位似多边形的有关概念.
2)通过图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化规律.
重点
掌握位似图像的性质,会画位似图形.
难点
理解位似图形的坐标变换规律.
观察下面四组图形有哪些相似点?
下面两个多边形相似,将两个图形的顶点相连,观察发现连接的直线相交于点O.
, ,,,,有什么关系?
如果两个相似多边形一组对应顶点P,P 所在的直线都过同一点O,且
OP =k· OP (k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心.其中k为相似多边形的相似比.
[提问]你觉得位似多边形有哪些性质?
1.两个图形相似.
2.对应点的连线相较于一点,对应边互相
平行或在同一直线上.
3.任意一对对应点到位似中心的距离之比等于相似比.
如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC上分别取点D,E,F,
使OD=2OA,OE=2OB,OF=2OC;
3)顺序连接D,E,F,则△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
你还有别的方法吗?
如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:1)画射线OA,OB,OC;
2)沿着射线OA,OB,OC反方向上分别取D,E,F,
使OD = 2OA,OE = 2OB,OF = 2OC;
3)顺序连接D,E,F,则△DEF与△ABC位似,相似比为2.
A
B
C
O
E
F
D
[提问]简述位似多边形的画法?
1) 确定位似中心.
2) 确定原图形的关键点(每对对应点都在位似中心的同侧或在位似中心的异侧).
3) 确定位似比.
4) 根据对应点所在直线经过位似中心且到位似中心的距离之比等于位似比,作出关键点的对应点,再按照原图的顺序连接各点.
例1 已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法一:△ABC与△DEF在同侧
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC上分别取点D,E,F,
使OA = 2OD,OB = 2OE,OC = 2OF;
3)顺序连接D,E,F,则△DEF与△ABC位似,位似比为1:2.
D
E
F
例1 已知点O在△ABC内,以点O为位似中心画一个三角形,使它与△ABC位似,且位似比为1:2.
A
B
C
画法二: △ABC与△DEF在异侧
解:1)画射线OA,OB,OC;
2)在射线OA,OB,OC反向延长线上分别取点D,E,F,使OA = 2OD,OB = 2OE,OC = 2OF;
3)顺序连接D,E,F,则△DEF与△ABC位似,位似比为1:2.
D
F
E
1. 下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点到位似中心的距离之比等于相比.其中正确的序号是( )
A.② B.①② C.③④ D.②③④
【详解】③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,但没有对应边平行(或在同一条直线上),那么这两个图形不一定位似图形,此项错误;
2.下列各组图形中不是位似图形的是()
3.如图,以点为位似中心,将△OAB放大后得到△OCD,,则____.
4.如图,在△ABC中,DE∥AB,DE分别与AC,BC交于D,E两点.若,AC=3,则DC=_____.
在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0), A(3,0), B(2,3)
(1)将点O,A,B的横坐标、纵坐标都乘2,得到三个点,以这三个点位为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比.
x
y
O
2
4
-2
-4
2
4
A
B
A '
B '
6
位似,
位似中心为:原点O,
位似比为:1:2
在平面直角坐标系中,△OAB三个顶点的坐标分别为O(0,0), A(3,0), B(2,3)
(2)将点O,A,B的横坐标、纵坐标都乘-2,得到三个点,以这三个点位为顶点的三角形与△OAB位似吗?如果位似,指出位似中心和相似比.
x
y
O
2
4
-2
-4
2
4
-2
-4
A
B
A '
B '
位似,
位似中心为:原点O,
位似比为:1:2
在平面直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k(k≠0),所对应的图形与原图形位似,位似中心是坐标原点,它们的相似比位|k|.
例2 在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),
B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使它
与四边形OABC的相似是2:3.
画法一:如右图所示,
解:将四边形OABC各顶点的坐标都乘 ;
在平面直角坐标系中描点O(0,0), A'(4,0),B'(2,4)C'(-2, 2);
在平面直角坐标系中描点A',B',C',用线段顺次连接O,A',B',C'.
例2 在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(6,0),
B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使它
与四边形OABC的相似是2:3.
画法二:如右图所示,
解:将四边形OABC各顶点的坐标都乘-;
在平面直角坐标系中描点O(0,0), A''(-4,0),
B''(-2,-4),C''(-2,-2);
在平面直角坐标系中描点A'',B'',C'',用线段顺次连接O,A'',B'',C''.
1)在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2)当位似图形在原点同侧时,相似比为 k,与它对应的点的坐标为 (kx,ky) ;
当位似图形在原点两侧时,相似比为-k,与它对应的点的坐标为 (-kx,-ky) .
3)当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的k倍.
1.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点E′的坐标为( )
A.(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
【详解】根据题意可知,点E的对应点E′的坐标是E(﹣4,2)的坐标同时乘以2或-2,
所以点E′的坐标为(8,-4)或(-8,4).故选B.
2.如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,
在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
A.(2,1) B.(2,0) C.(3,3) D.(3,1)
【详解】由题意得,△ODC∽△OBA,相似比是∴
又OB=6,AB=3,∴OD=2,CD=1,∴点C的坐标为:(2,1),故选A.
3.如图,正方形OABC 与正方形ODEF是位似图,点O为位似中心,位似比为 2:3 ,点A的坐标为(0,2),则点E的坐标是 ____.
【详解】解:∵正方形OABC 与正方形ODEF是位似图,位似比为 2:3 ,
∴OA:OD=2:3,
∵点A 的坐标为(0,2),即OA=2,
∴OD=3,DE=EF=3,
故点E的坐标是(3,3).
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若DE=7.5,则AB=_____.
【详解】解:∵A(1.5,0),D(4.5,0)∴==,
∵△ABC与△DEF位似,原点O是位似中心,
∴==, ∴AB=DE=×7.5=2.5.
5.如图,△ ABO三个顶点的坐标分别为A(﹣2,4),B(﹣4,0),O(0,0),以原点O为位似中心,画出一个三角形,使它与△ ABO的位似比为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
