2.2基本不等式 课件(共25张PPT)
文档属性
| 名称 | 2.2基本不等式 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 15:58:54 | ||
图片预览







文档简介
(共25张PPT)
2.2基本不等式
一
二
三
教学目标
掌握基本不等式,了解基本不等式的证明过程
理解基本不等式的取最值成立条件
(一正二定三相等)
利用基本不等式解决简单的最值问题
教学目标
难点
重点
易错点
会标
2002年在北京召开的第24届国际数学家大会会标
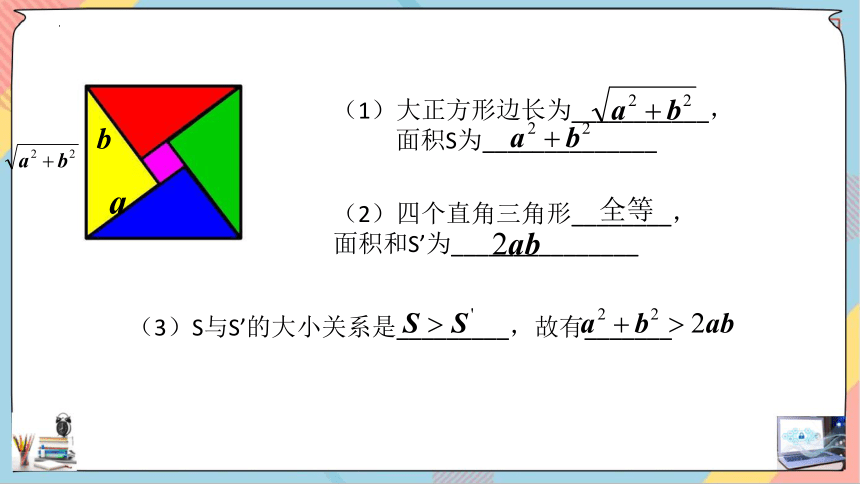
思考1:这图案中含有哪些几何图形?
思考2:你能发现图案中的相等关系或不等关系吗?
(1)大正方形边长为___________,
面积S为______________
(2)四个直角三角形________,
面积和S’为_______________
(3)S与S’的大小关系是_________,故有_______
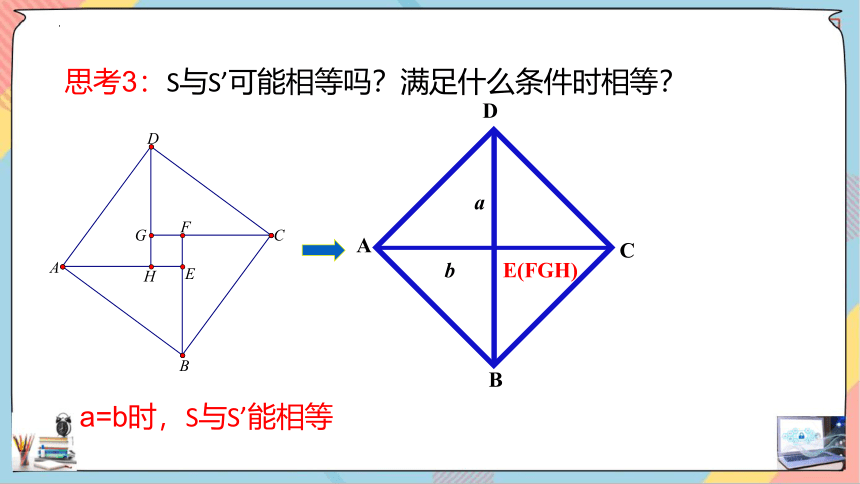
思考3:S与S’可能相等吗?满足什么条件时相等?
A
D
C
B
H
F
G
E
A
B
C
D
E(FGH)
a
b
a=b时,S与S’能相等
重要不等式: 一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立。
文字叙述为:
两数的平方和不小于它们积的2倍.
我们知道,乘法公式在代数式的运算中有重要作用。那么,是否也有一些不等式,它们在解决不等式问题时有着与乘法公式类似的重要作用呢?本节就来研究这个问题。
新课讲授
新课讲授
通常称不等式(1)为基本不等式,其中,叫做正数a,b的算术平均数,正数a,b的几何平均数。
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
即:
上面通过考察的特殊情形获得了基本不等式.能否直接利用不等式的性质推导出基本不等式呢?下面我们来分析一下.
要证 ,①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤成立,当且仅当时,⑤中的等号成立.
只要把上述过程倒过来,就能直接推出基本不等式了.
基本不等式的证明
代数法
基本不等式
基本不等式的证明
用圆的性质证明
B
C
A
D
E
a
b
O
AB为圆O的直径。用,b表示线段AC,BC
OD=______
CD=______
OD_____CD
≥
“半径不小于半弦”
例1 已知求的最小值.
解:∵∴
当且仅当即时,等号成立,因此所求的最小值为2.
在本题的解答中,我们不仅明确了有而且给出了“当且仅当即时,等号成立”,这是为了说明2是的一个取值.想一想,当时,成立吗?这时能说是的最小值吗?
例2 已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值
证明:∵都是正数,∴
(1)当积等于定值时,∴当且仅当时,上式等号成立.
于是,当时,和有最小值.
积定和最小
例2 已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值
证明:∵都是正数,∴
(2)当和等于定值时,
∴
当且仅当上式等号成立.
于是,当时,积有最大值
和定积最大
【例】已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
【证明】所以
(1)等于定值P时, ,所以
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,所以
,当且仅当时,上式等号成立,此时有最大值
最值定理及其应用
①当时,,,
当且仅当时,等号成立.
②当时,,
当且仅当时,等号成立.
最值定理及其应用
常见题型分类
题型一:对基本不等式的理解
例1 不等式+中,等式成立的条件是( )
A. B. C. D.
D
变1 (多选)已知且,则下列不等式成立的是( )
A. B.C. D.
BC
题型二:利用基本不等式比较大小
例2 设(、为互不相等的正实数),,则与的大小关系是( )
A. B. C. D.
A
题型二:利用基本不等式比较大小
变2 若,,且,则,,,中最大的是( ).
A. B. C. D.
D
∵,,且,
∴
∴四个数中最大的应从,中选择.
而
又∵,,∴
∴即
∴最大
题型三:利用基本不等式证明不等式
例3 已知均为正数且求证:.
证明:
∴
当且仅当时,等号成立.
∴.
题型三:利用基本不等式证明不等式
变3-1 已知且求证:.
题型三:利用基本不等式证明不等式
变3-2 已知求证:.
题型三:利用基本不等式证明不等式
变3-3 已知求证:.
证明:∵
∴利用基本不等式有:
∴
∴.
当且仅当时等号成立.
课堂小结
1、利用基本不等式求最值时,要注意
2、已知 x, y 都是正数, P, S 是常数.
(1) xy=P x+y≥2 P (当且仅当 x=y 时, 取“=”号).
(2) x+y=S xy≤ S2(当且仅当 x=y 时, 取“=”号).
1
4
一正二定三相等
知识像一艘船让它载着我们驶向理想的
……
谢谢
再 见
2.2基本不等式
一
二
三
教学目标
掌握基本不等式,了解基本不等式的证明过程
理解基本不等式的取最值成立条件
(一正二定三相等)
利用基本不等式解决简单的最值问题
教学目标
难点
重点
易错点
会标
2002年在北京召开的第24届国际数学家大会会标
思考1:这图案中含有哪些几何图形?
思考2:你能发现图案中的相等关系或不等关系吗?
(1)大正方形边长为___________,
面积S为______________
(2)四个直角三角形________,
面积和S’为_______________
(3)S与S’的大小关系是_________,故有_______
思考3:S与S’可能相等吗?满足什么条件时相等?
A
D
C
B
H
F
G
E
A
B
C
D
E(FGH)
a
b
a=b时,S与S’能相等
重要不等式: 一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立。
文字叙述为:
两数的平方和不小于它们积的2倍.
我们知道,乘法公式在代数式的运算中有重要作用。那么,是否也有一些不等式,它们在解决不等式问题时有着与乘法公式类似的重要作用呢?本节就来研究这个问题。
新课讲授
新课讲授
通常称不等式(1)为基本不等式,其中,叫做正数a,b的算术平均数,正数a,b的几何平均数。
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
即:
上面通过考察的特殊情形获得了基本不等式.能否直接利用不等式的性质推导出基本不等式呢?下面我们来分析一下.
要证 ,①
只要证 ②
要证②,只要证 ③
要证③,只要证 ④
要证④,只要证 ⑤
显然,⑤成立,当且仅当时,⑤中的等号成立.
只要把上述过程倒过来,就能直接推出基本不等式了.
基本不等式的证明
代数法
基本不等式
基本不等式的证明
用圆的性质证明
B
C
A
D
E
a
b
O
AB为圆O的直径。用,b表示线段AC,BC
OD=______
CD=______
OD_____CD
≥
“半径不小于半弦”
例1 已知求的最小值.
解:∵∴
当且仅当即时,等号成立,因此所求的最小值为2.
在本题的解答中,我们不仅明确了有而且给出了“当且仅当即时,等号成立”,这是为了说明2是的一个取值.想一想,当时,成立吗?这时能说是的最小值吗?
例2 已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值
证明:∵都是正数,∴
(1)当积等于定值时,∴当且仅当时,上式等号成立.
于是,当时,和有最小值.
积定和最小
例2 已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值
证明:∵都是正数,∴
(2)当和等于定值时,
∴
当且仅当上式等号成立.
于是,当时,积有最大值
和定积最大
【例】已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
【证明】所以
(1)等于定值P时, ,所以
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,所以
,当且仅当时,上式等号成立,此时有最大值
最值定理及其应用
①当时,,,
当且仅当时,等号成立.
②当时,,
当且仅当时,等号成立.
最值定理及其应用
常见题型分类
题型一:对基本不等式的理解
例1 不等式+中,等式成立的条件是( )
A. B. C. D.
D
变1 (多选)已知且,则下列不等式成立的是( )
A. B.C. D.
BC
题型二:利用基本不等式比较大小
例2 设(、为互不相等的正实数),,则与的大小关系是( )
A. B. C. D.
A
题型二:利用基本不等式比较大小
变2 若,,且,则,,,中最大的是( ).
A. B. C. D.
D
∵,,且,
∴
∴四个数中最大的应从,中选择.
而
又∵,,∴
∴即
∴最大
题型三:利用基本不等式证明不等式
例3 已知均为正数且求证:.
证明:
∴
当且仅当时,等号成立.
∴.
题型三:利用基本不等式证明不等式
变3-1 已知且求证:.
题型三:利用基本不等式证明不等式
变3-2 已知求证:.
题型三:利用基本不等式证明不等式
变3-3 已知求证:.
证明:∵
∴利用基本不等式有:
∴
∴.
当且仅当时等号成立.
课堂小结
1、利用基本不等式求最值时,要注意
2、已知 x, y 都是正数, P, S 是常数.
(1) xy=P x+y≥2 P (当且仅当 x=y 时, 取“=”号).
(2) x+y=S xy≤ S2(当且仅当 x=y 时, 取“=”号).
1
4
一正二定三相等
知识像一艘船让它载着我们驶向理想的
……
谢谢
再 见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
