2.2基本不等式 课件(共20张PPT)
文档属性
| 名称 | 2.2基本不等式 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
2.2.1 基本不等式
学习目标
1.能够推导并掌握基本不等式,理解基本不等式的几何意义,并掌握不等式中“≥”取等号的条件;
2.掌握基本不等式 ;会应
用基本不等式求一些函数的最值能够解决一些简单的实际问题
3.核心素养:数学抽象、逻辑推理、数学运算.
复习导入
重要不等式:一般地,
当且仅当a=b时,等号成立
特别地,如果a>0,b>0,我们用,,可得
当且仅当a=b时,等号成立
当通常把上式称为基本不等式
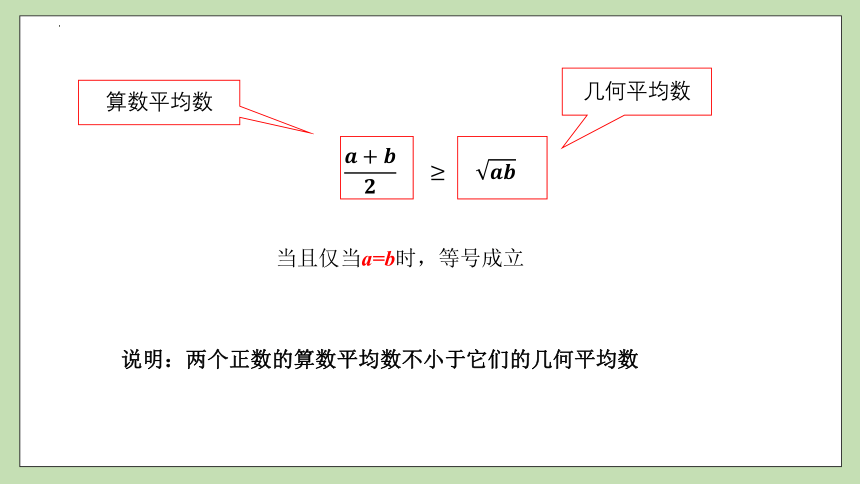
说明:两个正数的算数平均数不小于它们的几何平均数
复习导入
当且仅当a=b时,等号成立
说明:两个正数的算数平均数不小于它们的几何平均数
算数平均数
几何平均数
重要不等式与基本不等式的比较
适用范围
文字叙述
“=”成立条件
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
分析法
问题
证明不等式:
探究点 利用基本不等式证明简单不等式
求证:
探究点 利用基本不等式证明简单不等式
试一试:能否从几何的角度解释基本不等式?
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
几何意义:半径不小于半弦长
当点C在什么位置时OD=CD?
此时a与b的关系是?
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
A
B
C
D
E
a
b
O
例1.已知求的最小值.
解:∵∴
当且仅当即时,等号成立,因此所求的最小值为2.
在本题的解答中,我们不仅明确了有而且给出了“当且仅当即时,等号成立”,这是为了说明2是的一个取值.
想一想,当时,成立吗?这时能说是的最小值吗?
例2.已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
证明:∵都是正数,∴
(1)当积等于定值时,∴
积定和最小
当且仅当时,上式等号成立.
于是,当时,和有最小值.
已知都是正数,求证:
(2)如果和等于定值,那么当时,积有最大值
和定积最大
当且仅当上式等号成立.
于是,当时,积有最大值
证明:(2)当和等于定值时,
∴
1.已知a,b,c都是正数,求证:
(1) (a+b)(b+c)(c+a)≥8abc;
(2) (a+b+c)(++)≥9.
方
法
总结
数学思想 之 转化与化归
问
题
分
析
(1) 提示: (a+b)≥2; (b+c)≥2; (c+a)≥2
(2) (a+b+c)(++)=++
=3+()+()+()≥3+2+2+2=9.
基本不等式从一侧到另一侧,本质上是一种放大或缩小;当一侧为定值时,即为另一侧的一个最值;当然,先要满足取等条件.
2. (1) 已知x>0,则y=的最小值为 ;
(2) 已知x>1,则y=x+的最小值为 ;
(3) 已知0方
法
总结
数学思想 之 转化与化归
问
题
解
析
(1) y=3+(x+) ≥3+4=7 (2)y=(x-1)+ +1 ≥3
(3) y=x(3-2x) =≤=
(1)变形后局部可用基本不等式;
(2)与 (3)根据和或积的结构特征,可先配凑,再用基本不等式.
3.已知a>0,b>0,若不等式+≥恒成立,求m的
最大值.
方
法
总结
数学思想 之 极端思想 + 转化与化归
问
题
分
析
由+≥恒成立得m≤()(a+4b)恒成立;
而()(a+4b)=8+(+)≥8+8=16(当a=4b时取等号)
所以, m的最大值为16.
先将恒成立问题转化为求最值问题,再根据目标式的结构特点,局部使用基本不等式求得最值.
4.已知a+b=2,b>0,求+的最小值.
方
法
总结
数学思想 之 分类讨论 + 逆向思维
问
题
分
析
1)当02)当a<02时, ==+()≥-+1=;
所以, m的最小值为.
1.目标式含有绝对值的,要分类讨论; 2. 根据结构的需要,对常数1可以作逆向代换,以迎合基本不等式一侧积为常数的需要.
常用变形和结论
1.所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,达到放缩的效果。
2.要先观察题中要证明不等式的结构特征,若不能直接使用基本不等式证明,则考虑对代数式进行拆项、变形、配凑等,使之转化为能使用基本不等式的形式.
3.累加法是不等式性质的应用,也是证明不等式的一种常用方法。注意多次运用基本不等式时是否能同时取等号.
利用基本不等式证明不等式的方法
课堂小结
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
2.2.1 基本不等式
学习目标
1.能够推导并掌握基本不等式,理解基本不等式的几何意义,并掌握不等式中“≥”取等号的条件;
2.掌握基本不等式 ;会应
用基本不等式求一些函数的最值能够解决一些简单的实际问题
3.核心素养:数学抽象、逻辑推理、数学运算.
复习导入
重要不等式:一般地,
当且仅当a=b时,等号成立
特别地,如果a>0,b>0,我们用,,可得
当且仅当a=b时,等号成立
当通常把上式称为基本不等式
说明:两个正数的算数平均数不小于它们的几何平均数
复习导入
当且仅当a=b时,等号成立
说明:两个正数的算数平均数不小于它们的几何平均数
算数平均数
几何平均数
重要不等式与基本不等式的比较
适用范围
文字叙述
“=”成立条件
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
证明:要证
只要证
①
要证①,只要证
②
要证②,只要证
③
显然, ③是成立的.当且仅当a=b时, ③中的等号成立.
分析法
问题
证明不等式:
探究点 利用基本不等式证明简单不等式
求证:
探究点 利用基本不等式证明简单不等式
试一试:能否从几何的角度解释基本不等式?
②如何用a, b表示CD CD=______
①如何用a, b表示OD OD=______
③OD与CD的大小关系怎样 OD_____CD
≥
几何意义:半径不小于半弦长
当点C在什么位置时OD=CD?
此时a与b的关系是?
如图, AB是圆的直径, O为圆心,点C是AB上一点, AC=a, BC=b. 过点C作垂直于AB的弦DE,连接AD、BD、OD.
A
B
C
D
E
a
b
O
例1.已知求的最小值.
解:∵∴
当且仅当即时,等号成立,因此所求的最小值为2.
在本题的解答中,我们不仅明确了有而且给出了“当且仅当即时,等号成立”,这是为了说明2是的一个取值.
想一想,当时,成立吗?这时能说是的最小值吗?
例2.已知都是正数,求证:
(1)如果积等于定值,那么当时,和有最小值;
证明:∵都是正数,∴
(1)当积等于定值时,∴
积定和最小
当且仅当时,上式等号成立.
于是,当时,和有最小值.
已知都是正数,求证:
(2)如果和等于定值,那么当时,积有最大值
和定积最大
当且仅当上式等号成立.
于是,当时,积有最大值
证明:(2)当和等于定值时,
∴
1.已知a,b,c都是正数,求证:
(1) (a+b)(b+c)(c+a)≥8abc;
(2) (a+b+c)(++)≥9.
方
法
总结
数学思想 之 转化与化归
问
题
分
析
(1) 提示: (a+b)≥2; (b+c)≥2; (c+a)≥2
(2) (a+b+c)(++)=++
=3+()+()+()≥3+2+2+2=9.
基本不等式从一侧到另一侧,本质上是一种放大或缩小;当一侧为定值时,即为另一侧的一个最值;当然,先要满足取等条件.
2. (1) 已知x>0,则y=的最小值为 ;
(2) 已知x>1,则y=x+的最小值为 ;
(3) 已知0
法
总结
数学思想 之 转化与化归
问
题
解
析
(1) y=3+(x+) ≥3+4=7 (2)y=(x-1)+ +1 ≥3
(3) y=x(3-2x) =≤=
(1)变形后局部可用基本不等式;
(2)与 (3)根据和或积的结构特征,可先配凑,再用基本不等式.
3.已知a>0,b>0,若不等式+≥恒成立,求m的
最大值.
方
法
总结
数学思想 之 极端思想 + 转化与化归
问
题
分
析
由+≥恒成立得m≤()(a+4b)恒成立;
而()(a+4b)=8+(+)≥8+8=16(当a=4b时取等号)
所以, m的最大值为16.
先将恒成立问题转化为求最值问题,再根据目标式的结构特点,局部使用基本不等式求得最值.
4.已知a+b=2,b>0,求+的最小值.
方
法
总结
数学思想 之 分类讨论 + 逆向思维
问
题
分
析
1)当0
所以, m的最小值为.
1.目标式含有绝对值的,要分类讨论; 2. 根据结构的需要,对常数1可以作逆向代换,以迎合基本不等式一侧积为常数的需要.
常用变形和结论
1.所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,达到放缩的效果。
2.要先观察题中要证明不等式的结构特征,若不能直接使用基本不等式证明,则考虑对代数式进行拆项、变形、配凑等,使之转化为能使用基本不等式的形式.
3.累加法是不等式性质的应用,也是证明不等式的一种常用方法。注意多次运用基本不等式时是否能同时取等号.
利用基本不等式证明不等式的方法
课堂小结
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
