生活中的一次函数
图片预览


文档简介
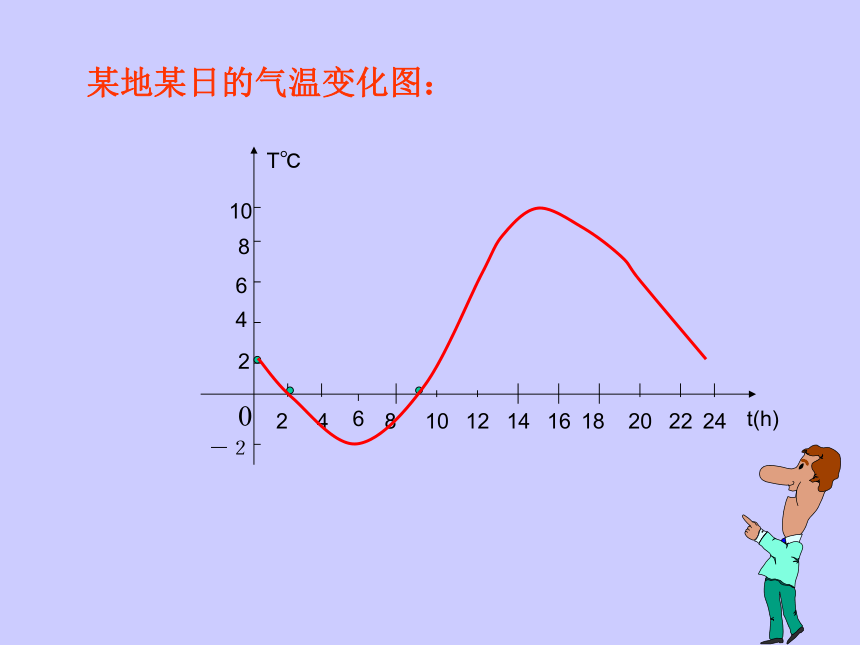
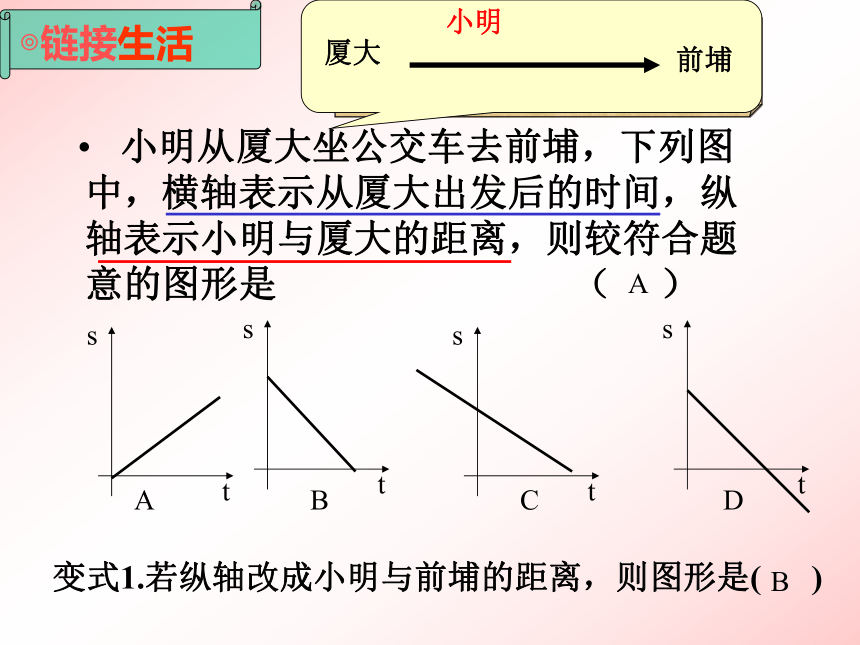
课件31张PPT。24681012141618202224246810T℃-20某地某日的气温变化图:t(h)生活中的一次函数ts 小明从厦大坐公交车去前埔,下列图中,横轴表示从厦大出发后的时间,纵轴表示小明与厦大的距离,则较符合题意的图形是 ( )
ABCD变式1.若纵轴改成小明与前埔的距离,则图形是( )AB横轴与纵轴的含义
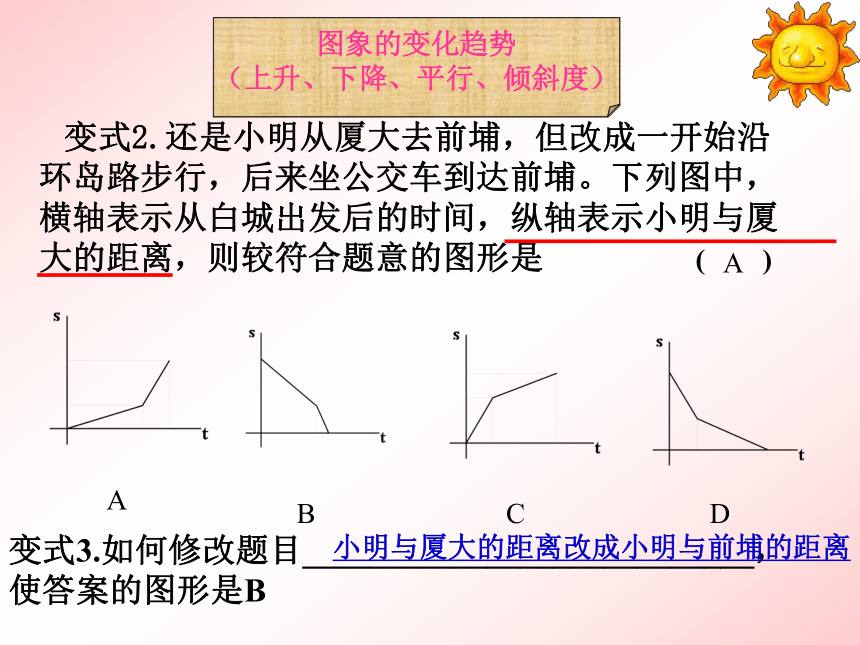
起点、终点、交点变式2.还是小明从厦大去前埔,但改成一开始沿环岛路步行,后来坐公交车到达前埔。下列图中,横轴表示从白城出发后的时间,纵轴表示小明与厦大的距离,则较符合题意的图形是 ( )
变式3.如何修改题目___________________________,使答案的图形是BA小明与厦大的距离改成小明与前埔的距离图象的变化趋势
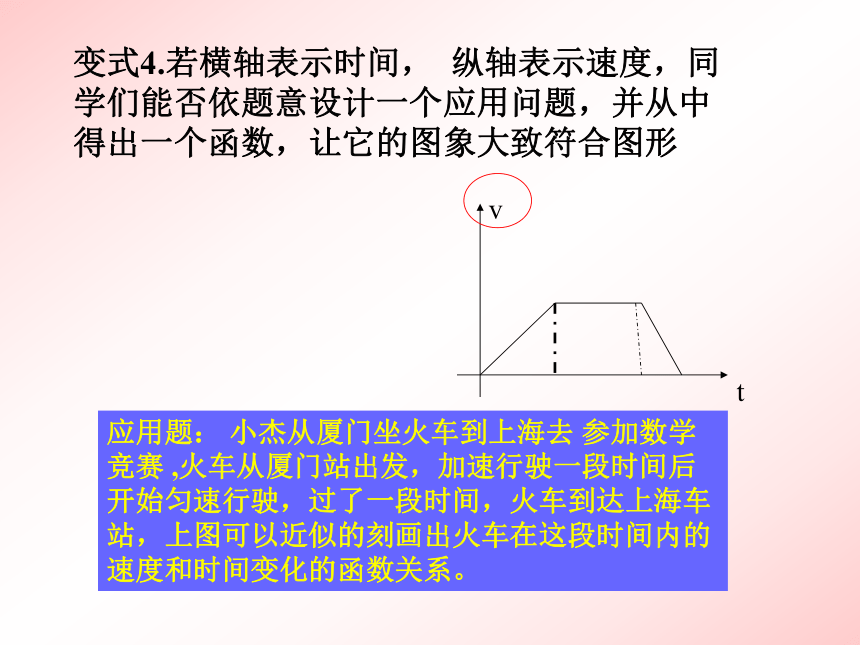
(上升、下降、平行、倾斜度)变式4.若横轴表示时间, 纵轴表示速度,同学们能否依题意设计一个应用问题,并从中得出一个函数,让它的图象大致符合图形应用题: 小杰从厦门坐火车到上海去 参加数学竞赛 ,火车从厦门站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达上海车站,上图可以近似的刻画出火车在这段时间内的速度和时间变化的函数关系。题后小结在观察函数图象主要看图形中的哪几个关键地方?3)图象的变化趋势
(上升、下降、平行、倾斜度)1) 两坐标轴的含义;2)关键点:起点、终点、交点
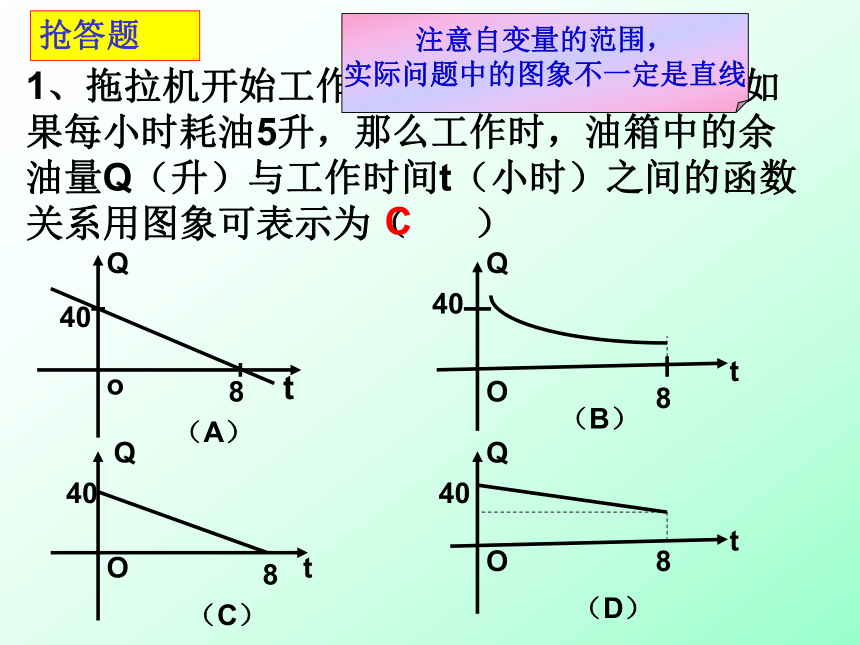
1、拖拉机开始工作时,油箱中有油40升,如果每小时耗油5升,那么工作时,油箱中的余油量Q(升)与工作时间t(小时)之间的函数关系用图象可表示为( )tQtQotQtQ(A)(B)(C)(D)408408408408OOOC抢答题注意自变量的范围,
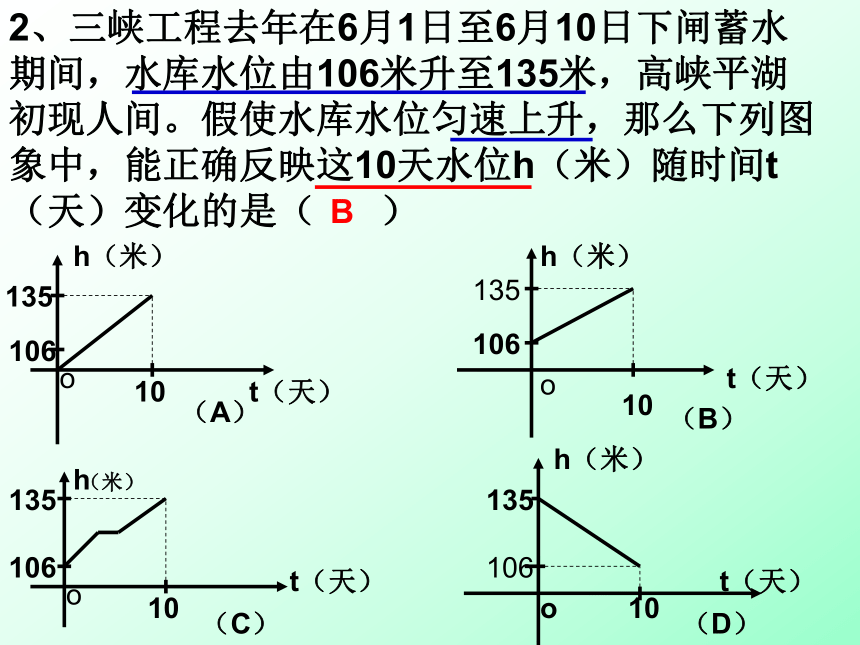
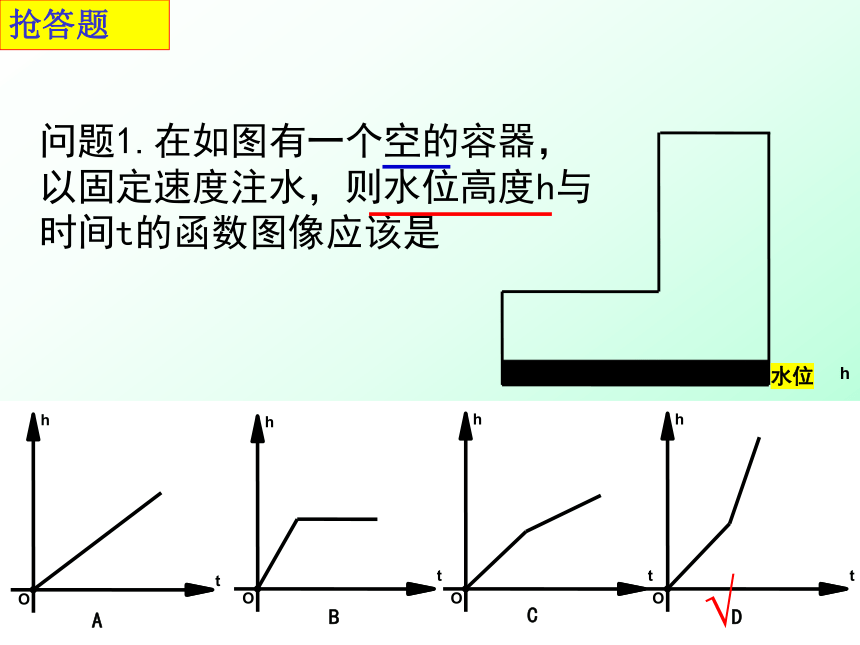
实际问题中的图象不一定是直线2、三峡工程去年在6月1日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡平湖初现人间。假使水库水位匀速上升,那么下列图象中,能正确反映这10天水位h(米)随时间t(天)变化的是( )t(天)h(米)t(天)h(米)t(天)ht(天)h(米)(米)oooo106135101061351061351010106135(A)(B)(C)(D)10B问题1.在如图有一个空的容器,以固定速度注水,则水位高度h与时间t的函数图像应该是抢答题√ 观察与思考·根据图象寻找你能观察到的所有信息: A车、B车同地出发,
前往80千米的目的地2、谁出发的早?早多少时
间?从哪可看出?观察与思考 3、甲地到乙地的路程有多远?从哪可看出这一点?4、从哪可看出A车追上了B 车? 用了多少时间?走了多少路程?(即当x取何值时, yA =yB ?)
1、图中的横坐标和纵坐标
各表示什么含义?
·观察与思考5、什么时候B车在A车前面?
什么时候B车在A车后面?
从图上怎么看? 6、你能从图上看出哪车的速度快?两条直线的倾斜程度
表示了什么意义?7、两车行驶的路程分别用yA 、 y B 表示, y A 、 y B
(km)与时间x(h)之间的函数关系式 是什么? (即当x取何值时, yB < yA ?)(即当x取何值时, y B > y A ?)y=40x-120y=10x8. 问A、B两车哪辆车先到60千米处,此时两车相距多少千米?解:由图可知,A车先到60千米处,将y=60,代入y=40x-120,x=4.5将x=4.5代入y=10x中,y=45所以此时两车相距15千米。y=40x-120y=10xy=?y=10xy=40x-1201、若不解方程组,你能得到以下方程组的解吗?2、若不解不等式 ,你能得到
以下不等式的解吗?
(1)10x>40x-120
(2)10x<40x-120(y B > yA )( y B < yA )图象中交点坐标就
是方程组的解利用函数图象来比较
大小,上大下小题后小结:3、从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题
的方法?1) 图象法;2)数形结合法1、在观察图形时主要看图形中的哪几个关键地方? 1) 两坐标轴的含义;2)关键点 3)变化趋势
4)图象的高低; 5)自变量的范围2、利用函数的图象我们刚才解决了哪几个问题? 1)求方程组的交点坐标;2)求不等式的解集; 美国某空军加油机接到命令,立即给一架正在飞往中国北京的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
空中加油
运输机加油机 俄罗斯某空军加油机接到命令,立即给一架正在飞往中国张家界的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?空中加油
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.(3)运输飞机加完油后,以原速继续飞行,需11分钟到达目的地,油料是否够用?说明理由.运输机加油机 俄罗斯某空军加油机接到命令,立即给一架正在飞往中国张家界的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;空中加油
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.解:(2)因图象过点(0 , 40)及点(10 , 6 9 ),代入得所以 Q1=2.9t+40 (0≤t ≤10)图象为线段想想(3)运输飞机加完油后,以原速继续飞行,需11分钟到达目的地,油料是否够用?说明理由.解:(3)根据图像可知
运输飞机的耗油量为每分钟0.1吨.∴10分钟耗油量为:
11×60×0.1=66吨∴油够用.<69吨.运输机原本剩油:加油机输入:10分钟后剩油量:10分钟内用油:动脑筋40306970-69=1(吨) 小明在移动公司办理了某种手机话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 医药公司开发了一种预防流感的新药,在试验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后,
(1)服药后______ 时,血液含药量最高。
(2)当x≤2时y与x之间的函数
关系式是 。
(3)当x≥2时y与x之间的函数
关系式是 。
(4)小组探究:如果每毫升血液中含药量
4毫克或4毫克以上时,治疗疾病有效,那么这个有效时间是 小时。
X(时)Y(毫克)65y=3xy=﹣x+832O2小时4
1.能从图象中获取信息(注意弄清楚坐标轴的 意义,抓住一些关键性的点,理解函数图象的变化趋势,注意自变量的取值范围);
2.能用一次函数解决一些实际问题。
3. 能用待定系数法求一次函数的解析式; 如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:1)乙出发时,与甲相距 km2)行走一段时间后,乙的自行车发生故障停下来修理,修车时间为 h3)乙从出发起,经过 h与甲相遇;4)甲的速度为 km/h , 乙骑车的速度为 km/h5)甲行走的路程s(千米)与时间t(小时)之间的函数关系式是 6)如果乙的自行车不出故障,则乙出发后经过 h与甲相遇,相遇后离乙的出发点 km,并在图中标出其相遇点。1012.5515s=5t+10(t≥0)115A相遇点为A品龙井 浙江移动公司手机的A类收费标准是:不管通话时间多长,每部手机每月必须缴月租费50元,另外每通话1分钟收0.4元;B类收费标准是:没有月租费,但每通话1分钟收0.6元.试问小芸爸爸选择哪类收费标准合算?解:设小芸爸爸每月要通话x分钟,A类、B类标准
收费分别为yA、yB,则:
yA=50+0.4x yB =0.6x
(1)、令yA> yB,即50+0.4x > 0.6x时,解得:x <250
说明通话时间少于250分钟选择B类合算;
(2)、令yA= yB,即50+0.4x = 0.6x时,解得:x = 250
说明通话时间等于250分钟选择A类、B类一样;
(3)、令yA< yB,即50+0.4x < 0.6x时,解得:x > 250
说明通话时间大于250分钟选择A类合算。对与实际问题进行:
收集数据;
画出函数的图象;
判断函数的类型;
求出解析式.就是一个建立数学模型的过程. 4月1日(星期天),是小杰的生日,爸爸和小杰打的到SM买生日礼物。出租车的收费标准是:3千米以内(含3千米)都收8元,超过3千米,每增加1千米就收2元。
(1)试写出乘出租车所需要的费用y(元)与行驶的路程
x千米之间的函数关系式;(要分成两种情况进行讨论)
⑵ 你能用图象表示出费用和行程之间的关系吗?(3)小杰家到SM有8千米,小杰身上有19元零花钱,
够不够付出租车费,你能利用图象来分析这个问题吗?
ABCD变式1.若纵轴改成小明与前埔的距离,则图形是( )AB横轴与纵轴的含义
起点、终点、交点变式2.还是小明从厦大去前埔,但改成一开始沿环岛路步行,后来坐公交车到达前埔。下列图中,横轴表示从白城出发后的时间,纵轴表示小明与厦大的距离,则较符合题意的图形是 ( )
变式3.如何修改题目___________________________,使答案的图形是BA小明与厦大的距离改成小明与前埔的距离图象的变化趋势
(上升、下降、平行、倾斜度)变式4.若横轴表示时间, 纵轴表示速度,同学们能否依题意设计一个应用问题,并从中得出一个函数,让它的图象大致符合图形应用题: 小杰从厦门坐火车到上海去 参加数学竞赛 ,火车从厦门站出发,加速行驶一段时间后开始匀速行驶,过了一段时间,火车到达上海车站,上图可以近似的刻画出火车在这段时间内的速度和时间变化的函数关系。题后小结在观察函数图象主要看图形中的哪几个关键地方?3)图象的变化趋势
(上升、下降、平行、倾斜度)1) 两坐标轴的含义;2)关键点:起点、终点、交点
1、拖拉机开始工作时,油箱中有油40升,如果每小时耗油5升,那么工作时,油箱中的余油量Q(升)与工作时间t(小时)之间的函数关系用图象可表示为( )tQtQotQtQ(A)(B)(C)(D)408408408408OOOC抢答题注意自变量的范围,
实际问题中的图象不一定是直线2、三峡工程去年在6月1日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡平湖初现人间。假使水库水位匀速上升,那么下列图象中,能正确反映这10天水位h(米)随时间t(天)变化的是( )t(天)h(米)t(天)h(米)t(天)ht(天)h(米)(米)oooo106135101061351061351010106135(A)(B)(C)(D)10B问题1.在如图有一个空的容器,以固定速度注水,则水位高度h与时间t的函数图像应该是抢答题√ 观察与思考·根据图象寻找你能观察到的所有信息: A车、B车同地出发,
前往80千米的目的地2、谁出发的早?早多少时
间?从哪可看出?观察与思考 3、甲地到乙地的路程有多远?从哪可看出这一点?4、从哪可看出A车追上了B 车? 用了多少时间?走了多少路程?(即当x取何值时, yA =yB ?)
1、图中的横坐标和纵坐标
各表示什么含义?
·观察与思考5、什么时候B车在A车前面?
什么时候B车在A车后面?
从图上怎么看? 6、你能从图上看出哪车的速度快?两条直线的倾斜程度
表示了什么意义?7、两车行驶的路程分别用yA 、 y B 表示, y A 、 y B
(km)与时间x(h)之间的函数关系式 是什么? (即当x取何值时, yB < yA ?)(即当x取何值时, y B > y A ?)y=40x-120y=10x8. 问A、B两车哪辆车先到60千米处,此时两车相距多少千米?解:由图可知,A车先到60千米处,将y=60,代入y=40x-120,x=4.5将x=4.5代入y=10x中,y=45所以此时两车相距15千米。y=40x-120y=10xy=?y=10xy=40x-1201、若不解方程组,你能得到以下方程组的解吗?2、若不解不等式 ,你能得到
以下不等式的解吗?
(1)10x>40x-120
(2)10x<40x-120(y B > yA )( y B < yA )图象中交点坐标就
是方程组的解利用函数图象来比较
大小,上大下小题后小结:3、从刚才的例子中我们应该总结一下, 我们用到了哪些解决问题
的方法?1) 图象法;2)数形结合法1、在观察图形时主要看图形中的哪几个关键地方? 1) 两坐标轴的含义;2)关键点 3)变化趋势
4)图象的高低; 5)自变量的范围2、利用函数的图象我们刚才解决了哪几个问题? 1)求方程组的交点坐标;2)求不等式的解集; 美国某空军加油机接到命令,立即给一架正在飞往中国北京的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
空中加油
运输机加油机 俄罗斯某空军加油机接到命令,立即给一架正在飞往中国张家界的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?空中加油
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.(3)运输飞机加完油后,以原速继续飞行,需11分钟到达目的地,油料是否够用?说明理由.运输机加油机 俄罗斯某空军加油机接到命令,立即给一架正在飞往中国张家界的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;空中加油
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.解:(2)因图象过点(0 , 40)及点(10 , 6 9 ),代入得所以 Q1=2.9t+40 (0≤t ≤10)图象为线段想想(3)运输飞机加完油后,以原速继续飞行,需11分钟到达目的地,油料是否够用?说明理由.解:(3)根据图像可知
运输飞机的耗油量为每分钟0.1吨.∴10分钟耗油量为:
11×60×0.1=66吨∴油够用.<69吨.运输机原本剩油:加油机输入:10分钟后剩油量:10分钟内用油:动脑筋40306970-69=1(吨) 小明在移动公司办理了某种手机话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 医药公司开发了一种预防流感的新药,在试验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后,
(1)服药后______ 时,血液含药量最高。
(2)当x≤2时y与x之间的函数
关系式是 。
(3)当x≥2时y与x之间的函数
关系式是 。
(4)小组探究:如果每毫升血液中含药量
4毫克或4毫克以上时,治疗疾病有效,那么这个有效时间是 小时。
X(时)Y(毫克)65y=3xy=﹣x+832O2小时4
1.能从图象中获取信息(注意弄清楚坐标轴的 意义,抓住一些关键性的点,理解函数图象的变化趋势,注意自变量的取值范围);
2.能用一次函数解决一些实际问题。
3. 能用待定系数法求一次函数的解析式; 如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:1)乙出发时,与甲相距 km2)行走一段时间后,乙的自行车发生故障停下来修理,修车时间为 h3)乙从出发起,经过 h与甲相遇;4)甲的速度为 km/h , 乙骑车的速度为 km/h5)甲行走的路程s(千米)与时间t(小时)之间的函数关系式是 6)如果乙的自行车不出故障,则乙出发后经过 h与甲相遇,相遇后离乙的出发点 km,并在图中标出其相遇点。1012.5515s=5t+10(t≥0)115A相遇点为A品龙井 浙江移动公司手机的A类收费标准是:不管通话时间多长,每部手机每月必须缴月租费50元,另外每通话1分钟收0.4元;B类收费标准是:没有月租费,但每通话1分钟收0.6元.试问小芸爸爸选择哪类收费标准合算?解:设小芸爸爸每月要通话x分钟,A类、B类标准
收费分别为yA、yB,则:
yA=50+0.4x yB =0.6x
(1)、令yA> yB,即50+0.4x > 0.6x时,解得:x <250
说明通话时间少于250分钟选择B类合算;
(2)、令yA= yB,即50+0.4x = 0.6x时,解得:x = 250
说明通话时间等于250分钟选择A类、B类一样;
(3)、令yA< yB,即50+0.4x < 0.6x时,解得:x > 250
说明通话时间大于250分钟选择A类合算。对与实际问题进行:
收集数据;
画出函数的图象;
判断函数的类型;
求出解析式.就是一个建立数学模型的过程. 4月1日(星期天),是小杰的生日,爸爸和小杰打的到SM买生日礼物。出租车的收费标准是:3千米以内(含3千米)都收8元,超过3千米,每增加1千米就收2元。
(1)试写出乘出租车所需要的费用y(元)与行驶的路程
x千米之间的函数关系式;(要分成两种情况进行讨论)
⑵ 你能用图象表示出费用和行程之间的关系吗?(3)小杰家到SM有8千米,小杰身上有19元零花钱,
够不够付出租车费,你能利用图象来分析这个问题吗?
