平行线的判定与性质
图片预览



文档简介
课件10张PPT。平行线的判定和性质(复习课)你有多少种画平行线的方法?问题:点P是直线AB外一点,求作一条直 线CD经过点P且与直线AB平行。
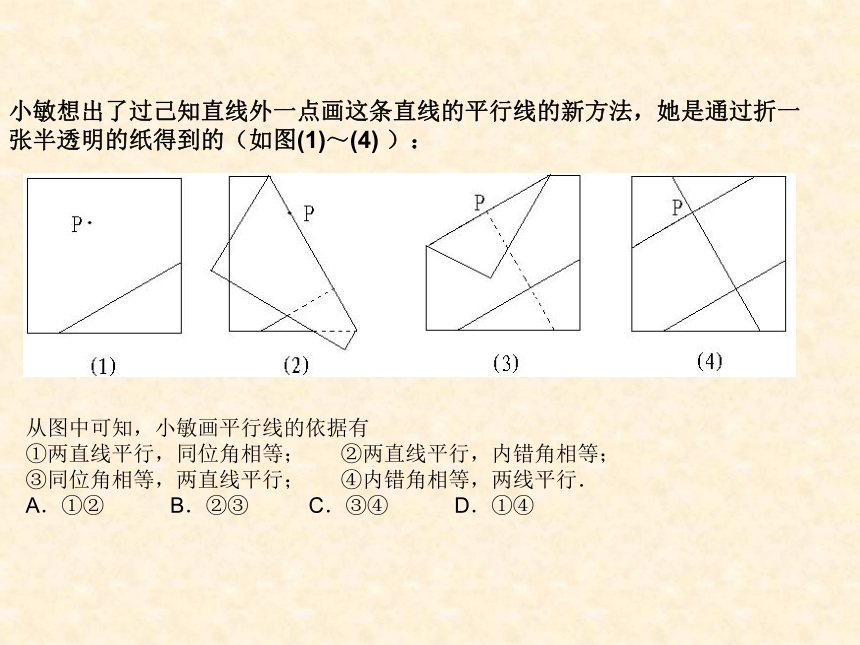
A小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ):
从图中可知,小敏画平行线的依据有
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两线平行.
A.①② B.②③ C.③④ D.①④
复习平行线的判定和性质平行线的判定:
平行线的性质:同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。两直线平行,同位角相等。两直线平行,内错角相等。两直线平行,同旁内角互补。判定:∵∠1+∠2=180°
∴a∥b (同旁内角互补,两直线平行)
性质:∵a∥b
∴∠1+∠2=180° (两直线平行,同旁内角互补)
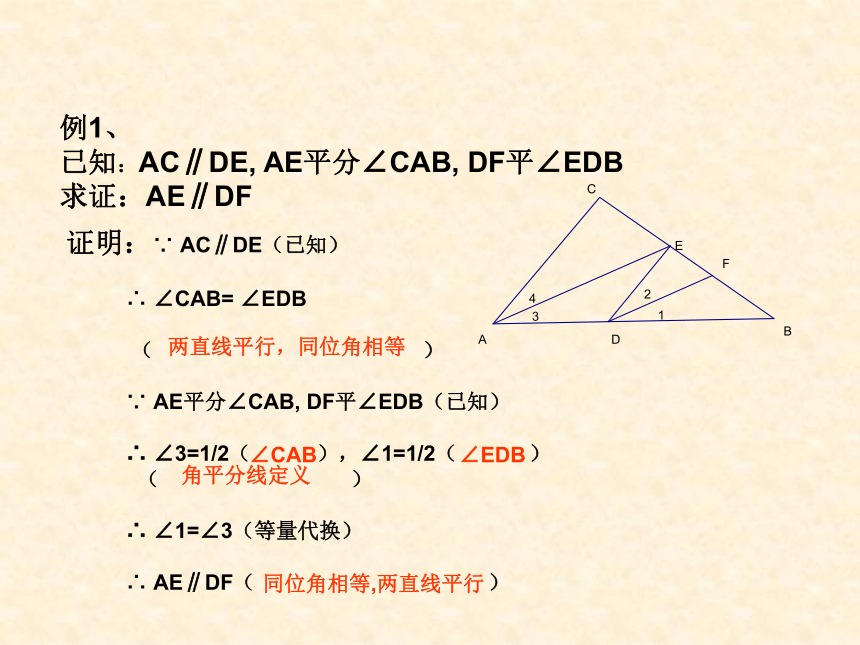
例1、
已知:AC∥DE, AE平分∠CAB, DF平∠EDB
求证:AE∥DF证明:∵ AC∥DE(已知)
∴ ∠CAB= ∠EDB
( )
∵ AE平分∠CAB, DF平∠EDB(已知)
∴ ∠3=1/2( ),∠1=1/2( )
( )
∴ ∠1=∠3(等量代换)
∴ AE∥DF( )两直线平行,同位角相等 ∠CAB∠EDB角平分线定义同位角相等,两直线平行例2:已知CD⊥AB, 点E是线段BC上一点,且EF⊥AB,
垂足分别为D、F。如果∠1=∠2,试判∠AGD
与∠ACB的关系,并加以说明。解: ∠AGD = ∠ACB。
理由如下:
∵ EF⊥AB ,CD⊥AB (已知)
∴ ∠BFE= ∠ BDC(垂直的定义)
∴ EF∥CD (同位角相等,两直线平行)
∴ ∠2=∠3 (两直线平行,同位角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠3(等量代换)
∴ DG∥BC(内错角相等,两直线平行)
∴ ∠AGD = ∠ACB(两直线平行,同位角相等) 如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠21、台球桌面上的角练一练 如图所示,已知直线MN分别与直线AB、CD相交于E、F,AB∥CD,EG平分∠BEF,FH平分∠CFE.
求证:EG∥FH.小结这节课你学到了哪些知识?布置作业: P35 第6 、8题如图:利用三角板我们可以作出直线AB∥ CD,依据是:同位角相等,两直线平行。21思考:利用三角板,我们能不能用“内错角相等,两直线平行”作出平行线呢?
利用“同旁内角互补,两直线平行”又该如何作呢?
A小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4) ):
从图中可知,小敏画平行线的依据有
①两直线平行,同位角相等; ②两直线平行,内错角相等;
③同位角相等,两直线平行; ④内错角相等,两线平行.
A.①② B.②③ C.③④ D.①④
复习平行线的判定和性质平行线的判定:
平行线的性质:同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。两直线平行,同位角相等。两直线平行,内错角相等。两直线平行,同旁内角互补。判定:∵∠1+∠2=180°
∴a∥b (同旁内角互补,两直线平行)
性质:∵a∥b
∴∠1+∠2=180° (两直线平行,同旁内角互补)
例1、
已知:AC∥DE, AE平分∠CAB, DF平∠EDB
求证:AE∥DF证明:∵ AC∥DE(已知)
∴ ∠CAB= ∠EDB
( )
∵ AE平分∠CAB, DF平∠EDB(已知)
∴ ∠3=1/2( ),∠1=1/2( )
( )
∴ ∠1=∠3(等量代换)
∴ AE∥DF( )两直线平行,同位角相等 ∠CAB∠EDB角平分线定义同位角相等,两直线平行例2:已知CD⊥AB, 点E是线段BC上一点,且EF⊥AB,
垂足分别为D、F。如果∠1=∠2,试判∠AGD
与∠ACB的关系,并加以说明。解: ∠AGD = ∠ACB。
理由如下:
∵ EF⊥AB ,CD⊥AB (已知)
∴ ∠BFE= ∠ BDC(垂直的定义)
∴ EF∥CD (同位角相等,两直线平行)
∴ ∠2=∠3 (两直线平行,同位角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠3(等量代换)
∴ DG∥BC(内错角相等,两直线平行)
∴ ∠AGD = ∠ACB(两直线平行,同位角相等) 如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠21、台球桌面上的角练一练 如图所示,已知直线MN分别与直线AB、CD相交于E、F,AB∥CD,EG平分∠BEF,FH平分∠CFE.
求证:EG∥FH.小结这节课你学到了哪些知识?布置作业: P35 第6 、8题如图:利用三角板我们可以作出直线AB∥ CD,依据是:同位角相等,两直线平行。21思考:利用三角板,我们能不能用“内错角相等,两直线平行”作出平行线呢?
利用“同旁内角互补,两直线平行”又该如何作呢?
