3.1 字母表示数 强化提优训练 (含答案) 2023-2024学年苏科版七年级数学上册
文档属性
| 名称 | 3.1 字母表示数 强化提优训练 (含答案) 2023-2024学年苏科版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 158.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 21:10:16 | ||
图片预览


文档简介
2023-2024学年苏科版七年级数学《3.1字母表示数》强化提优训练
(时间:100分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.下列式子,符合用字母表示数的书写格式的是( )
A.a÷3 B.2x C.a×3 D.
2.温度由t℃下降5℃后是( )
A.t+5℃ B.(t+5)℃ C.t﹣5℃ D.(t﹣5)℃
3.某省参加课改实验区初中毕业学业考试的学生约有15万人,其中男生约有a万人,则女生约有( )
A.(15+a)万人 B.(15-a)万人 C.15a万人 D.(a-15)万人
4.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( )
A.2n-2 B.2n C.2n+1 D.2n-1
5.若k袋苹果的质量为m千克,则x袋这样的苹果的质量为( )
A.千克 B.千克 C.千克 D.千克
6.一个两位数,其个位数是a,十位数是b.若把这个两位数的数字对调,所得两位数是( )
A.ab B.ba C.10a+b D.10b+a
7.一个运算程序输入x后,得到的结果是2x2-1,则这个运算程序是( )
A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2
C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘2
8.某商品打七折后价格为a元,则原价为( )
A.a元 B.a元 C.30%a元 D.a元
9.如图,一扇窗户的上部分是由4个完全相同的扇形组成的半圆,下部分是由4个完全相同的边长为a的小正方形组成的大正方形,做这扇窗户需要的材料总长为( )
A.15a B.15a+πa C.15a+πa2 D.πa+6a
第9题图 第10题图
10.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A. B. C. D.
二.填空题(每小题3分 共30分)
11、代数式5(a+b)的意义是______________
12、长方形的长是a米,宽比长的2倍少b米,则宽为___________米.
13、一批上衣的进价为每件a元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为__________元
14.棱长为a的正方体,它的表面积为_______.
15.甲、乙两地相距s km,两辆汽车分别从甲、乙两地同时出发,以a km/h,b km/h的平均速度相向而行,相遇时两车行驶的时间为________h.
16.“x的2倍与5的和”用字母表示为____.
17.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为____元.
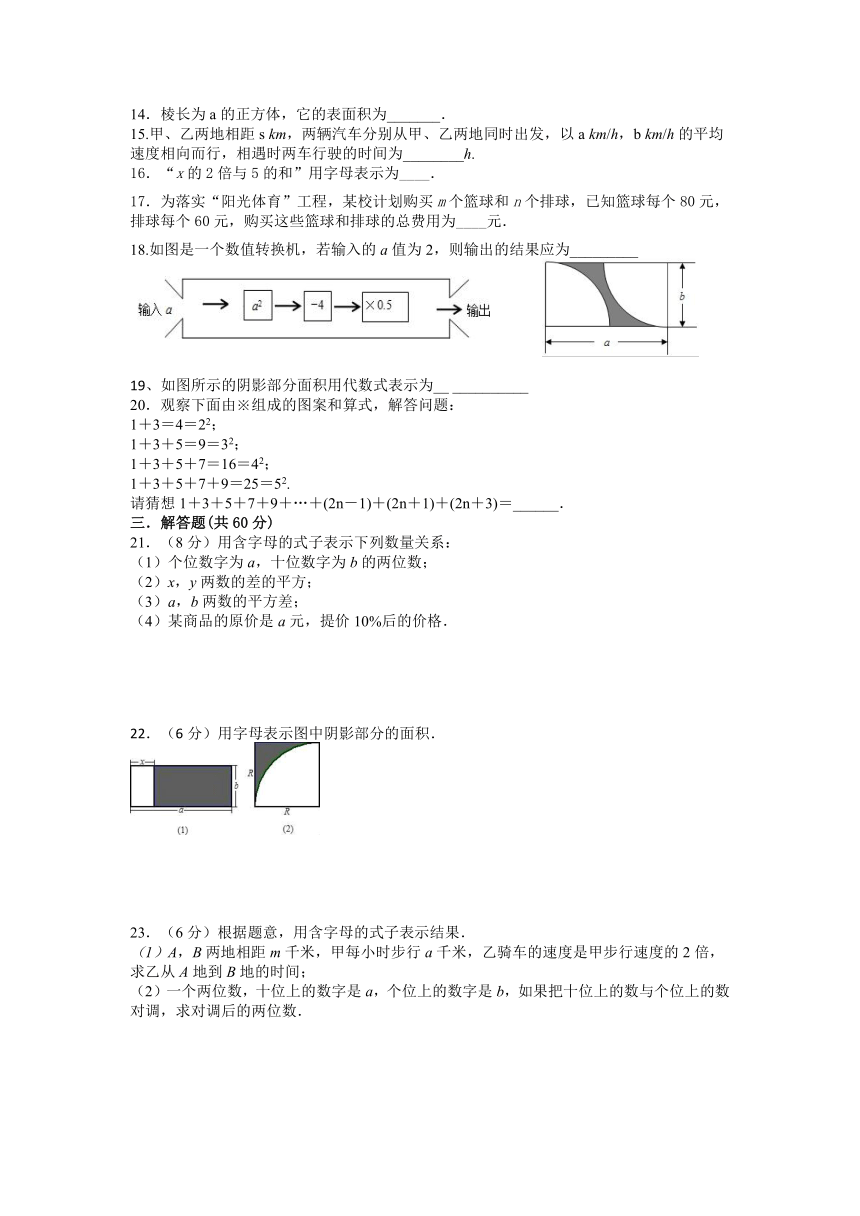
18.如图是一个数值转换机,若输入的a值为2,则输出的结果应为_________
19、如图所示的阴影部分面积用代数式表示为__ __________
20.观察下面由※组成的图案和算式,解答问题:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.
请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=______.
三.解答题(共60分)
21.(8分)用含字母的式子表示下列数量关系:
(1)个位数字为a,十位数字为b的两位数;
(2)x,y两数的差的平方;
(3)a,b两数的平方差;
(4)某商品的原价是a元,提价10%后的价格.
22.(6分)用字母表示图中阴影部分的面积.
23.(6分)根据题意,用含字母的式子表示结果.
(1)A,B两地相距m千米,甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,求乙从A地到B地的时间;
(2)一个两位数,十位上的数字是a,个位上的数字是b,如果把十位上的数与个位上的数对调,求对调后的两位数.
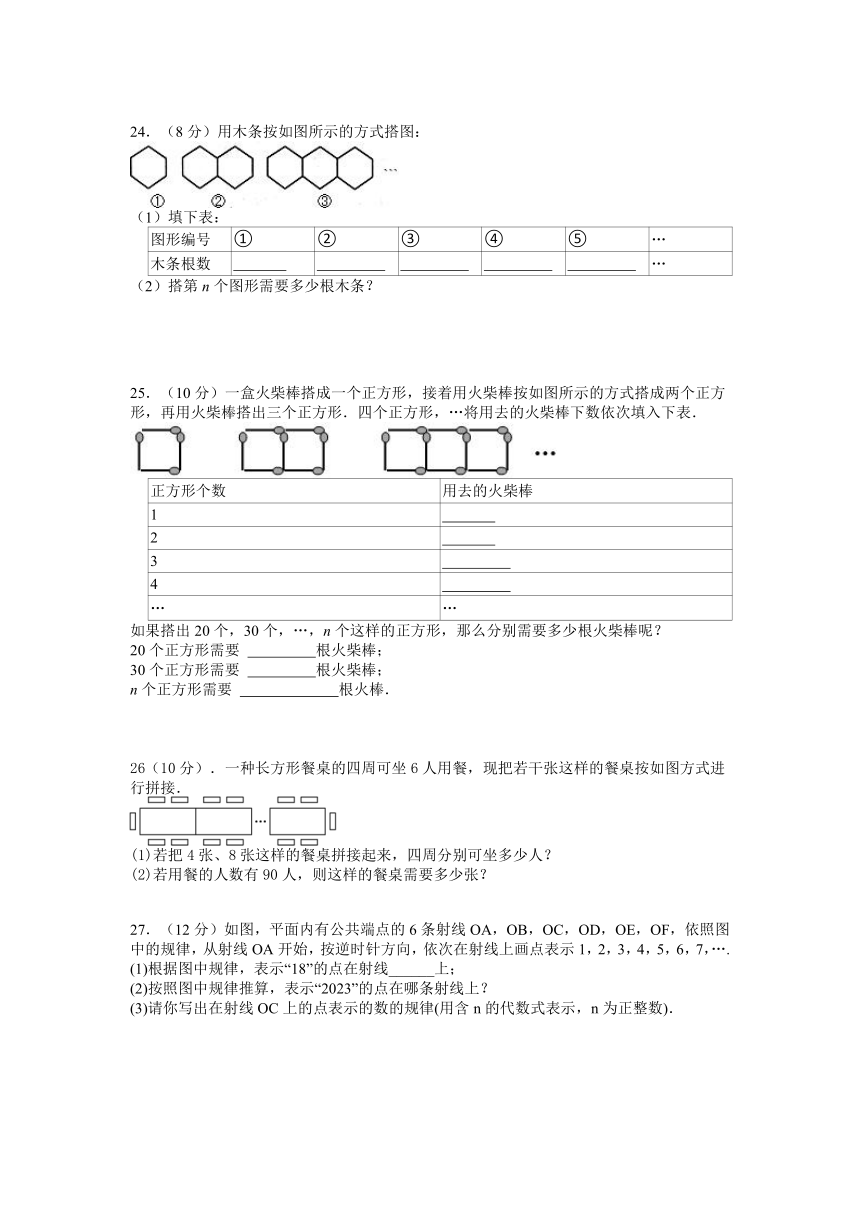
24.(8分)用木条按如图所示的方式搭图:
(1)填下表:
图形编号 ① ② ③ ④ ⑤ …
木条根数 …
(2)搭第n个图形需要多少根木条?
25.(10分)一盒火柴棒搭成一个正方形,接着用火柴棒按如图所示的方式搭成两个正方形,再用火柴棒搭出三个正方形.四个正方形,…将用去的火柴棒下数依次填入下表.
正方形个数 用去的火柴棒
1
2
3
4
… …
如果搭出20个,30个,…,n个这样的正方形,那么分别需要多少根火柴棒呢?
20个正方形需要 根火柴棒;
30个正方形需要 根火柴棒;
n个正方形需要 根火棒.
26(10分).一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
27.(12分)如图,平面内有公共端点的6条射线OA,OB,OC,OD,OE,OF,依照图中的规律,从射线OA开始,按逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,….
(1)根据图中规律,表示“18”的点在射线______上;
(2)按照图中规律推算,表示“2023”的点在哪条射线上?
(3)请你写出在射线OC上的点表示的数的规律(用含n的代数式表示,n为正整数).
教师样卷
一.选择题(每小题3分 共30分)
1.下列式子,符合用字母表示数的书写格式的是( D )
A.a÷3 B.2x C.a×3 D.
2.温度由t℃下降5℃后是( D )
A.t+5℃ B.(t+5)℃ C.t﹣5℃ D.(t﹣5)℃
3.某省参加课改实验区初中毕业学业考试的学生约有15万人,其中男生约有a万人,则女生约有( B )
A.(15+a)万人 B.(15-a)万人 C.15a万人 D.(a-15)万人
4.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( A )
A.2n-2 B.2n C.2n+1 D.2n-1
5.若k袋苹果的质量为m千克,则x袋这样的苹果的质量为( C )
A.千克 B.千克 C.千克 D.千克
6.一个两位数,其个位数是a,十位数是b.若把这个两位数的数字对调,所得两位数是( C )
A.ab B.ba C.10a+b D.10b+a
7.一个运算程序输入x后,得到的结果是2x2-1,则这个运算程序是( C )
A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2
C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘2
8.某商品打七折后价格为a元,则原价为( B )
A.a元 B.a元 C.30%a元 D.a元
9.如图,一扇窗户的上部分是由4个完全相同的扇形组成的半圆,下部分是由4个完全相同的边长为a的小正方形组成的大正方形,做这扇窗户需要的材料总长为( B )
A.15a B.15a+πa C.15a+πa2 D.πa+6a
第9题图 第10题图
10.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( B )
A. B. C. D.
二.填空题(每小题3分 共30分)
11、代数式5(a+b)的意义是__ a与b的和的5倍____________
12、长方形的长是a米,宽比长的2倍少b米,则宽为___(2a﹣b)________米.
13、一批上衣的进价为每件a元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为____0.9a _______元
14.棱长为a的正方体,它的表面积为___6a2_____.
15.甲、乙两地相距s km,两辆汽车分别从甲、乙两地同时出发,以a km/h,b km/h的平均速度相向而行,相遇时两车行驶的时间为________h.
16.“x的2倍与5的和”用字母表示为__2x+5__.
17.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为__(80m+60n)__元.
18.如图是一个数值转换机,若输入的a值为2,则输出的结果应为_____0_____
19、如图所示的阴影部分面积用代数式表示为__ ab﹣ __________
20.观察下面由※组成的图案和算式,解答问题:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.
请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=__(n+2)2______.
三.解答题(共60分)
21.(8分)用含字母的式子表示下列数量关系:
(1)个位数字为a,十位数字为b的两位数;
(2)x,y两数的差的平方;
(3)a,b两数的平方差;
(4)某商品的原价是a元,提价10%后的价格.
解:(1)10b+a.
(2)(x﹣y)2.
(3)a2﹣b2.
(4)(1+10%)a元.
22.(6分)用字母表示图中阴影部分的面积.
解:(1)阴影部分的面积=ab﹣bx;(2)阴影部分的面积=R2﹣πR2.
23.(6分)根据题意,用含字母的式子表示结果.
(1)A,B两地相距m千米,甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,求乙从A地到B地的时间;
(2)一个两位数,十位上的数字是a,个位上的数字是b,如果把十位上的数与个位上的数对调,求对调后的两位数.
解:(1)甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,
所以乙的速度是2a千米/时.所以乙从A地到B地的时间为.
(2)由题意,得对调后的两位数是10b+a.
24.(8分)用木条按如图所示的方式搭图:
(1)填下表:
图形编号 ① ② ③ ④ ⑤ …
木条根数 …
(2)搭第n个图形需要多少根木条?
解:第1个图形有6个, 第2个图形有2×6﹣1=11个, 第3个图形有3×6﹣2=16个
第4个图形有4×6﹣3=21个 第5个图形有5×6﹣4=26个
(1)故答案为:6,11,16,21,26
(2)第n个图形有6n﹣(n﹣1)=5n+1,故第n个图形有5n+1个小木条.
25.(10分)一盒火柴棒搭成一个正方形,接着用火柴棒按如图所示的方式搭成两个正方形,再用火柴棒搭出三个正方形.四个正方形,…将用去的火柴棒下数依次填入下表.
正方形个数 用去的火柴棒
1
2
3
4
… …
如果搭出20个,30个,…,n个这样的正方形,那么分别需要多少根火柴棒呢?
20个正方形需要 根火柴棒;
30个正方形需要 根火柴棒;
n个正方形需要 根火棒.
解:由图知:1个正方形需要3+1=4根火柴; 2个正方形需要3×2+1=7根火柴;
3个正方形需要3×3+1=10根火柴; 4个正方形需要3×4+1=13根火柴;
5个正方形需要3×5+1=16根火柴;...
20个正方形需要3×20+1=61根火柴; 30个正方形需要3×30+1=91根火柴;
n个正方形需要(3n+1)根火柴; 故答案为:7;10;13;61;91;(3n+1).
26(10分).一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
解:(1)1张长方形餐桌的四周可坐4+2=6(人),2张长方形餐桌的四周可坐4×2+2=10(人),3张长方形餐桌的四周可坐4×3+2=14(人),……n张长方形餐桌的四周可坐(4n+2)人,所以4张长方形餐桌的四周可坐4×4+2=18(人),8张长方形餐桌的四周可坐4×8+2=34(人).
(2)90-2=88(人),88÷4=22(张).答:这样的餐桌需要22张.
27.(12分)如图,平面内有公共端点的6条射线OA,OB,OC,OD,OE,OF,依照图中的规律,从射线OA开始,按逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,….
(1)根据图中规律,表示“18”的点在射线______上;
(2)按照图中规律推算,表示“2023”的点在哪条射线上?
(3)请你写出在射线OC上的点表示的数的规律(用含n的代数式表示,n为正整数).
解:根据观察,可发现规律:OA上的点表示的数是6n-5,OB上的点表示的数是6n-4,OC上的点表示的数是6n-3,OD上的点表示的数是6n-2,OE上的点表示的数是6n-1,OF上的点表示的数是6n.
(1)因为18是6的倍数,所以表示“18”的点在射线OF上.故答案为OF.
(2)因为2023÷6=337……1,所以表示“2017”的点在射线OA上.
(3)在射线OC上的点表示的数为6n-3(n为正整数).
(时间:100分钟 满分:120分)
一.选择题(每小题3分 共30分)
1.下列式子,符合用字母表示数的书写格式的是( )
A.a÷3 B.2x C.a×3 D.
2.温度由t℃下降5℃后是( )
A.t+5℃ B.(t+5)℃ C.t﹣5℃ D.(t﹣5)℃
3.某省参加课改实验区初中毕业学业考试的学生约有15万人,其中男生约有a万人,则女生约有( )
A.(15+a)万人 B.(15-a)万人 C.15a万人 D.(a-15)万人
4.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( )
A.2n-2 B.2n C.2n+1 D.2n-1
5.若k袋苹果的质量为m千克,则x袋这样的苹果的质量为( )
A.千克 B.千克 C.千克 D.千克
6.一个两位数,其个位数是a,十位数是b.若把这个两位数的数字对调,所得两位数是( )
A.ab B.ba C.10a+b D.10b+a
7.一个运算程序输入x后,得到的结果是2x2-1,则这个运算程序是( )
A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2
C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘2
8.某商品打七折后价格为a元,则原价为( )
A.a元 B.a元 C.30%a元 D.a元
9.如图,一扇窗户的上部分是由4个完全相同的扇形组成的半圆,下部分是由4个完全相同的边长为a的小正方形组成的大正方形,做这扇窗户需要的材料总长为( )
A.15a B.15a+πa C.15a+πa2 D.πa+6a
第9题图 第10题图
10.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A. B. C. D.
二.填空题(每小题3分 共30分)
11、代数式5(a+b)的意义是______________
12、长方形的长是a米,宽比长的2倍少b米,则宽为___________米.
13、一批上衣的进价为每件a元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为__________元
14.棱长为a的正方体,它的表面积为_______.
15.甲、乙两地相距s km,两辆汽车分别从甲、乙两地同时出发,以a km/h,b km/h的平均速度相向而行,相遇时两车行驶的时间为________h.
16.“x的2倍与5的和”用字母表示为____.
17.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为____元.
18.如图是一个数值转换机,若输入的a值为2,则输出的结果应为_________
19、如图所示的阴影部分面积用代数式表示为__ __________
20.观察下面由※组成的图案和算式,解答问题:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.
请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=______.
三.解答题(共60分)
21.(8分)用含字母的式子表示下列数量关系:
(1)个位数字为a,十位数字为b的两位数;
(2)x,y两数的差的平方;
(3)a,b两数的平方差;
(4)某商品的原价是a元,提价10%后的价格.
22.(6分)用字母表示图中阴影部分的面积.
23.(6分)根据题意,用含字母的式子表示结果.
(1)A,B两地相距m千米,甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,求乙从A地到B地的时间;
(2)一个两位数,十位上的数字是a,个位上的数字是b,如果把十位上的数与个位上的数对调,求对调后的两位数.
24.(8分)用木条按如图所示的方式搭图:
(1)填下表:
图形编号 ① ② ③ ④ ⑤ …
木条根数 …
(2)搭第n个图形需要多少根木条?
25.(10分)一盒火柴棒搭成一个正方形,接着用火柴棒按如图所示的方式搭成两个正方形,再用火柴棒搭出三个正方形.四个正方形,…将用去的火柴棒下数依次填入下表.
正方形个数 用去的火柴棒
1
2
3
4
… …
如果搭出20个,30个,…,n个这样的正方形,那么分别需要多少根火柴棒呢?
20个正方形需要 根火柴棒;
30个正方形需要 根火柴棒;
n个正方形需要 根火棒.
26(10分).一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
27.(12分)如图,平面内有公共端点的6条射线OA,OB,OC,OD,OE,OF,依照图中的规律,从射线OA开始,按逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,….
(1)根据图中规律,表示“18”的点在射线______上;
(2)按照图中规律推算,表示“2023”的点在哪条射线上?
(3)请你写出在射线OC上的点表示的数的规律(用含n的代数式表示,n为正整数).
教师样卷
一.选择题(每小题3分 共30分)
1.下列式子,符合用字母表示数的书写格式的是( D )
A.a÷3 B.2x C.a×3 D.
2.温度由t℃下降5℃后是( D )
A.t+5℃ B.(t+5)℃ C.t﹣5℃ D.(t﹣5)℃
3.某省参加课改实验区初中毕业学业考试的学生约有15万人,其中男生约有a万人,则女生约有( B )
A.(15+a)万人 B.(15-a)万人 C.15a万人 D.(a-15)万人
4.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( A )
A.2n-2 B.2n C.2n+1 D.2n-1
5.若k袋苹果的质量为m千克,则x袋这样的苹果的质量为( C )
A.千克 B.千克 C.千克 D.千克
6.一个两位数,其个位数是a,十位数是b.若把这个两位数的数字对调,所得两位数是( C )
A.ab B.ba C.10a+b D.10b+a
7.一个运算程序输入x后,得到的结果是2x2-1,则这个运算程序是( C )
A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2
C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘2
8.某商品打七折后价格为a元,则原价为( B )
A.a元 B.a元 C.30%a元 D.a元
9.如图,一扇窗户的上部分是由4个完全相同的扇形组成的半圆,下部分是由4个完全相同的边长为a的小正方形组成的大正方形,做这扇窗户需要的材料总长为( B )
A.15a B.15a+πa C.15a+πa2 D.πa+6a
第9题图 第10题图
10.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( B )
A. B. C. D.
二.填空题(每小题3分 共30分)
11、代数式5(a+b)的意义是__ a与b的和的5倍____________
12、长方形的长是a米,宽比长的2倍少b米,则宽为___(2a﹣b)________米.
13、一批上衣的进价为每件a元,在进价的基础上提高50%后作为零售价,由于季节原因,打6折促销,则打折后每件上衣的价格为____0.9a _______元
14.棱长为a的正方体,它的表面积为___6a2_____.
15.甲、乙两地相距s km,两辆汽车分别从甲、乙两地同时出发,以a km/h,b km/h的平均速度相向而行,相遇时两车行驶的时间为________h.
16.“x的2倍与5的和”用字母表示为__2x+5__.
17.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为__(80m+60n)__元.
18.如图是一个数值转换机,若输入的a值为2,则输出的结果应为_____0_____
19、如图所示的阴影部分面积用代数式表示为__ ab﹣ __________
20.观察下面由※组成的图案和算式,解答问题:
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52.
请猜想1+3+5+7+9+…+(2n-1)+(2n+1)+(2n+3)=__(n+2)2______.
三.解答题(共60分)
21.(8分)用含字母的式子表示下列数量关系:
(1)个位数字为a,十位数字为b的两位数;
(2)x,y两数的差的平方;
(3)a,b两数的平方差;
(4)某商品的原价是a元,提价10%后的价格.
解:(1)10b+a.
(2)(x﹣y)2.
(3)a2﹣b2.
(4)(1+10%)a元.
22.(6分)用字母表示图中阴影部分的面积.
解:(1)阴影部分的面积=ab﹣bx;(2)阴影部分的面积=R2﹣πR2.
23.(6分)根据题意,用含字母的式子表示结果.
(1)A,B两地相距m千米,甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,求乙从A地到B地的时间;
(2)一个两位数,十位上的数字是a,个位上的数字是b,如果把十位上的数与个位上的数对调,求对调后的两位数.
解:(1)甲每小时步行a千米,乙骑车的速度是甲步行速度的2倍,
所以乙的速度是2a千米/时.所以乙从A地到B地的时间为.
(2)由题意,得对调后的两位数是10b+a.
24.(8分)用木条按如图所示的方式搭图:
(1)填下表:
图形编号 ① ② ③ ④ ⑤ …
木条根数 …
(2)搭第n个图形需要多少根木条?
解:第1个图形有6个, 第2个图形有2×6﹣1=11个, 第3个图形有3×6﹣2=16个
第4个图形有4×6﹣3=21个 第5个图形有5×6﹣4=26个
(1)故答案为:6,11,16,21,26
(2)第n个图形有6n﹣(n﹣1)=5n+1,故第n个图形有5n+1个小木条.
25.(10分)一盒火柴棒搭成一个正方形,接着用火柴棒按如图所示的方式搭成两个正方形,再用火柴棒搭出三个正方形.四个正方形,…将用去的火柴棒下数依次填入下表.
正方形个数 用去的火柴棒
1
2
3
4
… …
如果搭出20个,30个,…,n个这样的正方形,那么分别需要多少根火柴棒呢?
20个正方形需要 根火柴棒;
30个正方形需要 根火柴棒;
n个正方形需要 根火棒.
解:由图知:1个正方形需要3+1=4根火柴; 2个正方形需要3×2+1=7根火柴;
3个正方形需要3×3+1=10根火柴; 4个正方形需要3×4+1=13根火柴;
5个正方形需要3×5+1=16根火柴;...
20个正方形需要3×20+1=61根火柴; 30个正方形需要3×30+1=91根火柴;
n个正方形需要(3n+1)根火柴; 故答案为:7;10;13;61;91;(3n+1).
26(10分).一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
解:(1)1张长方形餐桌的四周可坐4+2=6(人),2张长方形餐桌的四周可坐4×2+2=10(人),3张长方形餐桌的四周可坐4×3+2=14(人),……n张长方形餐桌的四周可坐(4n+2)人,所以4张长方形餐桌的四周可坐4×4+2=18(人),8张长方形餐桌的四周可坐4×8+2=34(人).
(2)90-2=88(人),88÷4=22(张).答:这样的餐桌需要22张.
27.(12分)如图,平面内有公共端点的6条射线OA,OB,OC,OD,OE,OF,依照图中的规律,从射线OA开始,按逆时针方向,依次在射线上画点表示1,2,3,4,5,6,7,….
(1)根据图中规律,表示“18”的点在射线______上;
(2)按照图中规律推算,表示“2023”的点在哪条射线上?
(3)请你写出在射线OC上的点表示的数的规律(用含n的代数式表示,n为正整数).
解:根据观察,可发现规律:OA上的点表示的数是6n-5,OB上的点表示的数是6n-4,OC上的点表示的数是6n-3,OD上的点表示的数是6n-2,OE上的点表示的数是6n-1,OF上的点表示的数是6n.
(1)因为18是6的倍数,所以表示“18”的点在射线OF上.故答案为OF.
(2)因为2023÷6=337……1,所以表示“2017”的点在射线OA上.
(3)在射线OC上的点表示的数为6n-3(n为正整数).
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
