2.1.1 平面及其表示法

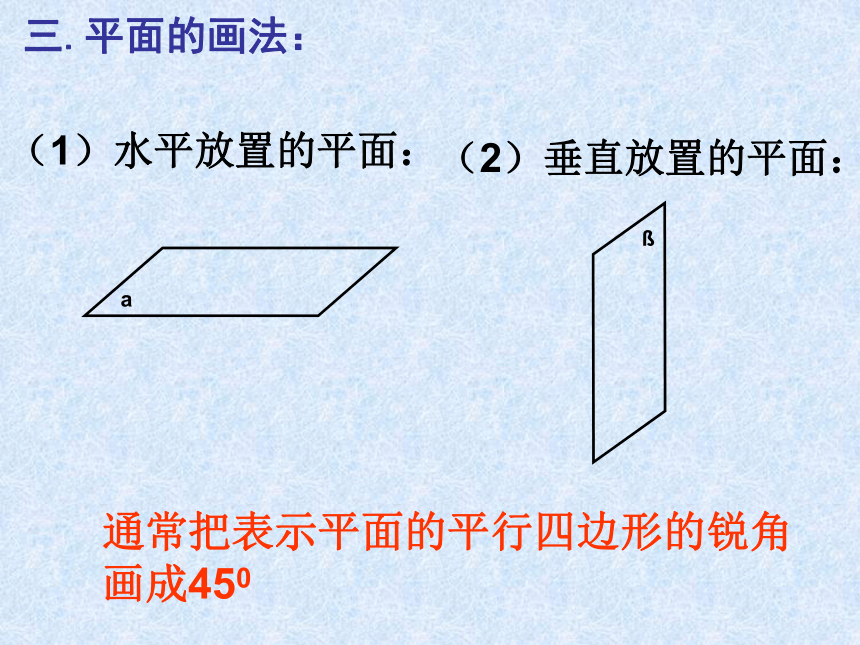
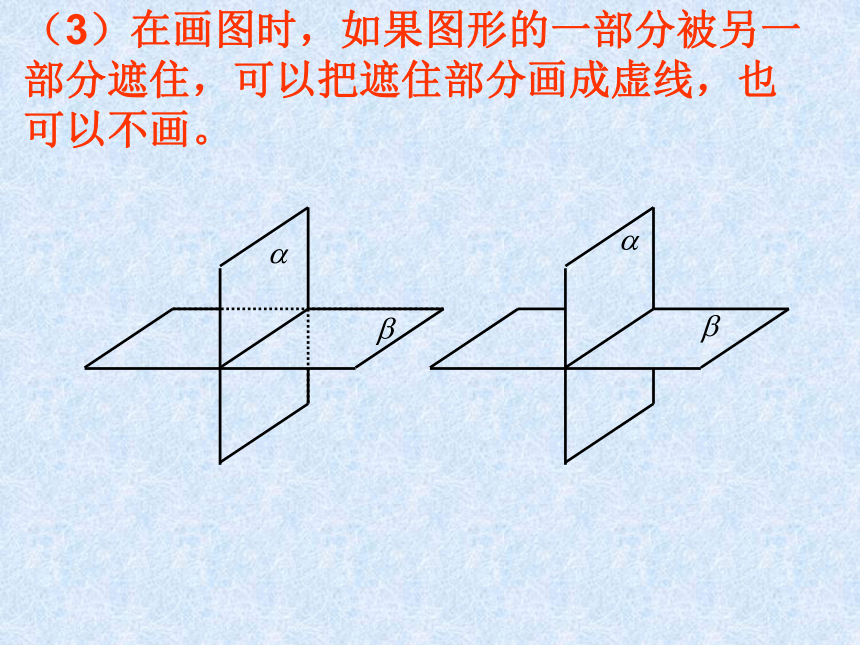
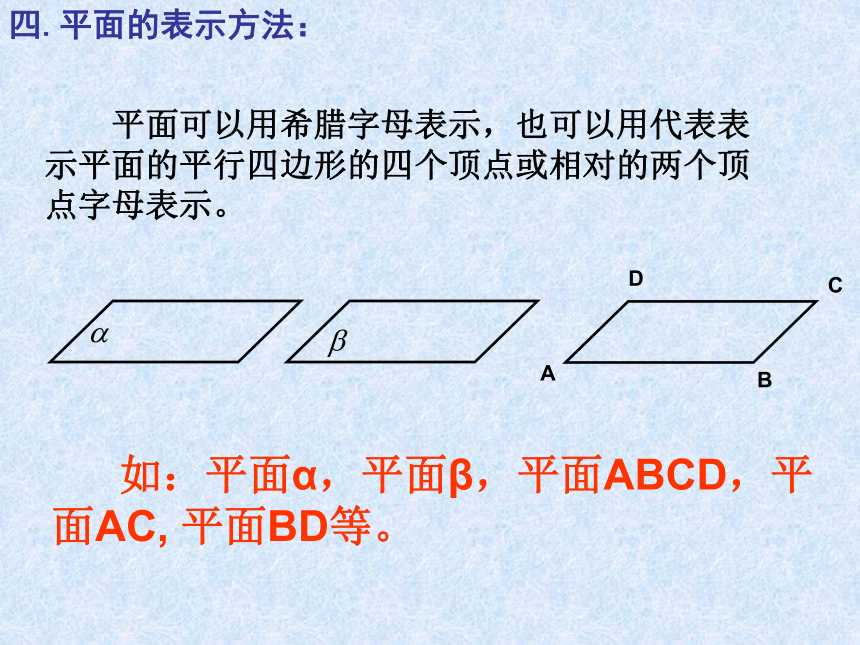
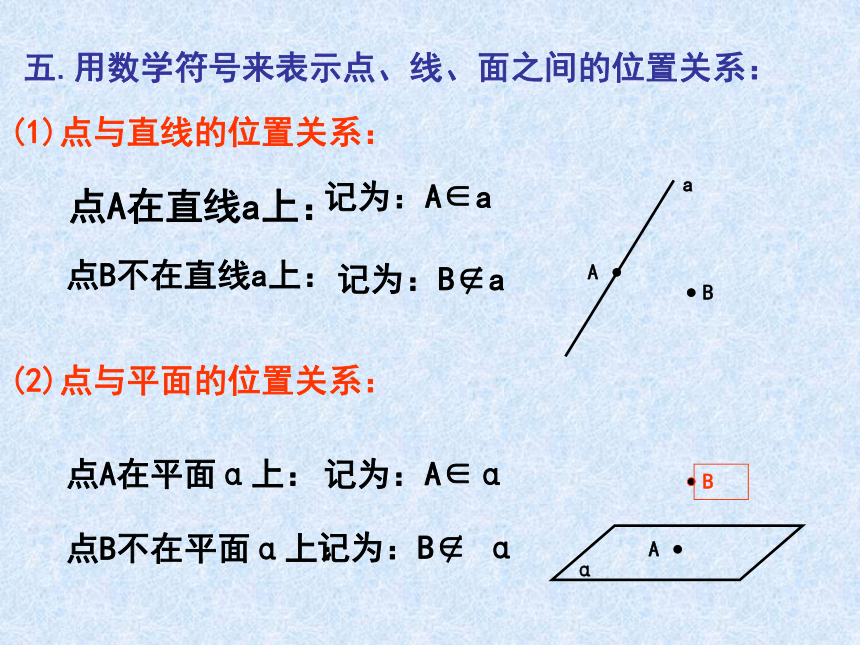
课件17张PPT。2.1.1 平面一.平面的概念：　　光滑的桌面、平静的湖面等都是我们熟悉的平面形象，数学中的平面概念是现实平面加以抽象的结果。二.平面的特征：　　平面没有大小、厚薄和宽窄，平面在空间是无限延伸的。三.平面的画法：（1）水平放置的平面：（2）垂直放置的平面：通常把表示平面的平行四边形的锐角画成450（3）在画图时，如果图形的一部分被另一部分遮住，可以把遮住部分画成虚线，也可以不画。四.平面的表示方法：　　平面可以用希腊字母表示，也可以用代表表示平面的平行四边形的四个顶点或相对的两个顶点字母表示。　　如：平面α，平面β，平面ABCD，平面AC, 平面BD等。五.用数学符号来表示点、线、面之间的位置关系： 点A在直线a上：记为：A∈a点B不在直线a上：　点A在平面α上：记为：A∈α点B不在平面α上：(1)点与直线的位置关系：(2)点与平面的位置关系：(3)直线与平面的位置关系： 直线a上的所有点都在平面α上，称直线a在平面α内，或称平面α通过直线a.记为： 直线a与平面α只有一个公共点A时，称直线a与平面α相交。　记为：a∩α＝A 直线a与平面α没有公共点时，称直线a与平面α平行。　记为：a∩α＝φ 或 a∥α.(4)平面与平面的位置关系：　　当平面α上的所有点都在平面β上时，称平面α与平面β重合。　　当两个不同平面α与平面β有公共点时，它们的公共点组成集合a，称平面α与平面β相交。　　　　记： α∩ β＝a。　　当平面α与平面β没有公共点时，称平面α与平面β平行。记： α∩ β＝φ或α ∥ β。五.用数学符号来表示点、线、面之间的位置关系：aA∈aA∈αb∩α＝Aa∩α＝φ 或 a∥αα∩β ＝aα∩ β＝φ
或α ∥ βΑ与β重合公理1.如果一条直线上两点在一个平面内，那么这条直线上的所有的点都在这个平面内（即直线在平面内）。观察下列问题，你能得到什么结论？公理1.如果一条直线上两点在一个平面内，那么这条直线上的所有的点都在这个平面内（即直线在平面内）。文字语言：图形语言：符号语言：公理2.过不在同一直线上的三点，有且只有一个平面.观察下列问题，你能得到什么结论_？文字语言：图形语言：符号语言：公理2.过不在同一直线上的三点，有且只有一个平面.公理3.如果两个不重合的平面有一个公共点，那么
这两个平面有且只有一条过该点的公共直线。观察下列问题，你能得到什么结论？天花板α墙面β墙面γ文字语言：图形语言：符号语言：公理3.如果两个不重合的平面有一个公共点，那么
这两个平面有且只有一条过该点的公共直线。（×）（×）（×）（×）推论1.一条直线和直线外一点唯一确定一个平面。推论2.两条相交直线唯一确定一个平面。推论3.两条平行直线唯一确定一个平面。公理3.不在同一直线上的三点唯一确定一个平面.