第5章相交线与平行线测试卷(含答案)
文档属性
| 名称 | 第5章相交线与平行线测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 20:30:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华师版七年级数学上学期单元测试卷
第5章 相交线与平行线
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.如图,直线AB,CD交于点O,若∠AOC增大50°,则∠BOD ( )
A.不变 B.增大50° C.减少50° D.增大130°
2.如图,直线a,b被直线c所截,则∠1与∠2是 ( )
A.内错角 B.同位角 C.对顶角 D.同旁内角
3.下列画出的直线a与b不一定平行的是 ( )
A B C D
4.如图,俄罗斯方块游戏中,图形A经过平行移动填补空位,则正确的平行移动方式是 ( )
A.先向右平行移动5格,再向下平行移动3格
B.先向右平行移动4格,再向下平行移动5格
C.先向右平行移动3格,再向下平行移动5格
D.先向右平行移动4格,再向下平行移动4格
5.如图,河道l的一侧有A,B两个村庄,现要铺设一条引水管道把河水引向A,B两村,下列四种方案中最节省材料的是 ( )
A B C D
6.如图,将三角板的直角顶点放在两条平行线中的直线AB上,若∠1=22°,则∠2的度数为 ( )
A.78° B.68° C.22° D.60°
7.下列说法正确的是 ( )
A.两直线的位置关系是平行、垂直或相交
B.在平面内,经过直线外一点,有无数条直线与这条直线平行
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
8.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,若∠COA=54°,OF平分∠EOD,则∠FOB等于 ( )
A.30° B.18° C.27° D.22°
9.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,则这两次拐弯的角度可能是 ( )
A.第一次向左拐50°,第二次向右拐50°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向右拐50°,第二次向右拐130°
D.第一次向左拐50°,第二次向左拐130°
10.如图,AB∥EF,∠C=90°,则α,β和γ的关系是 ( )
A.β=α+γ B.α+β+γ=180° C.α+β -γ=90° D.β+γ -α=180°
二、填空题(每小题3分,共15分)
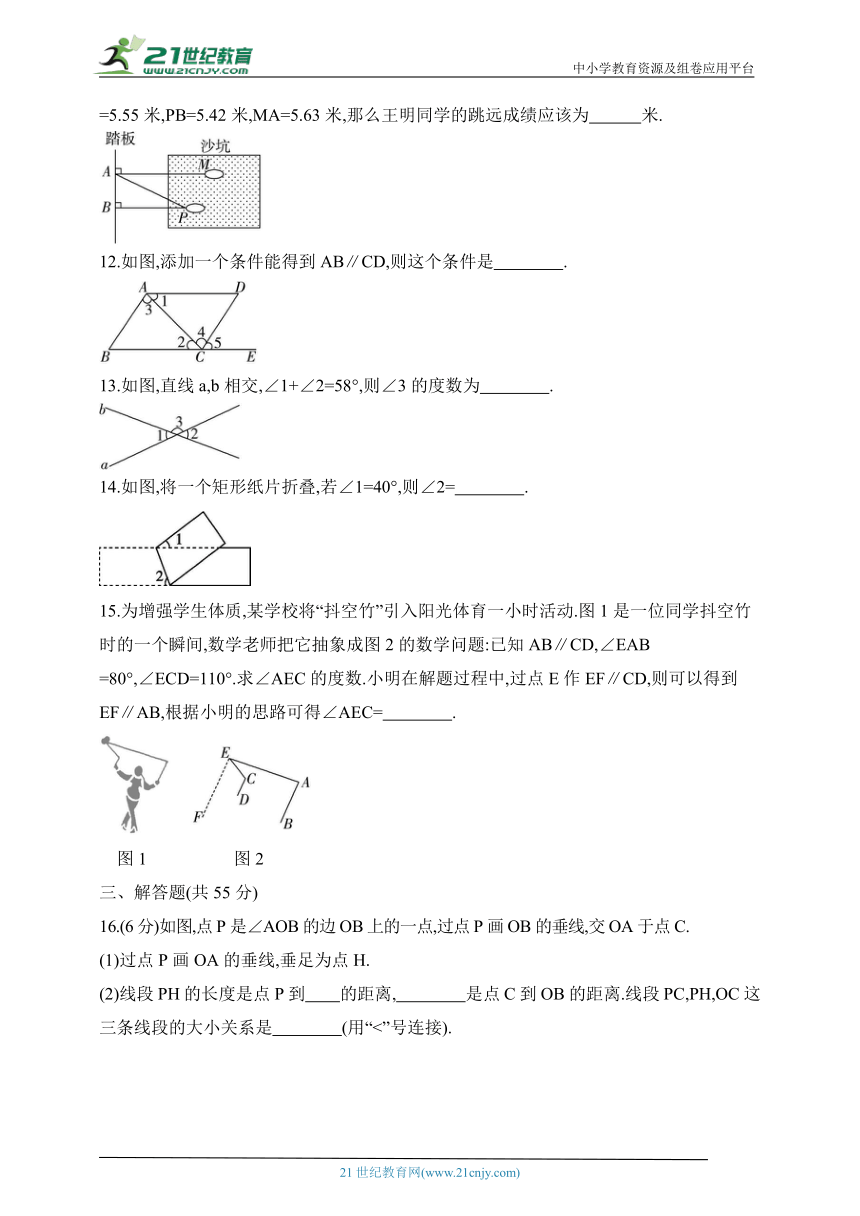
11.如图,是王明同学在跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA
=5.55米,PB=5.42米,MA=5.63米,那么王明同学的跳远成绩应该为 米.
12.如图,添加一个条件能得到AB∥CD,则这个条件是 .
13.如图,直线a,b相交,∠1+∠2=58°,则∠3的度数为 .
14.如图,将一个矩形纸片折叠,若∠1=40°,则∠2= .
15.为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB
=80°,∠ECD=110°.求∠AEC的度数.小明在解题过程中,过点E作EF∥CD,则可以得到EF∥AB,根据小明的思路可得∠AEC= .
图1 图2
三、解答题(共55分)
16.(6分)如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为点H.
(2)线段PH的长度是点P到 的距离, 是点C到OB的距离.线段PC,PH,OC这三条线段的大小关系是 (用“<”号连接).
17.(8分)如图,∠AOB的一边OA为平面镜,∠AOB=37°36',在OB上有一点E,从E点射出一束光线(入射光线)经OA上一点D反射,反射光线DC恰好与OB平行(入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠1=∠3),求∠DEB的度数.
18.(8分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
19.(10分)如图,l1∥l2∥l3,点A,M,B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,
∠2=70°.求∠CMD的度数.
20.(11分)(1)如图1,已知∠1=∠2,∠B=∠C,则AB与CD平行吗
请补全下面的解答过程(填理由或数学式).
解:∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换),
∴CE∥BF( ),
∴∠ =∠BFD( ).
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( ).
(2)如图2,已知AD∥BE,∠1=∠2,则∠A与∠E相等吗 试说明理由.
图1 图2
21.(12分)(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(2)如图2,AD∥BC,点P在射线OM上运动,若∠ADP=∠α,∠BCP=∠β.
①当点P在A,B两点之间运动时,∠CPD,∠α,∠β之间的数量关系为 .
②当点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请写出∠CPD,∠α,
∠β之间的数量关系,并说明理由.
图1 图2
参考答案与解析
1.B 因为∠AOC与∠BOD互为对顶角,所以∠AOC=∠BOD,所以当∠AOC增大50°时,∠BOD也增大50°.故选B.
2.A
3.A 选项A中,直线a与b不一定平行.
4.D
5.C
6.B 如图,根据题意知,∠3=90°-∠1=90°-22°=68°.由平行可知∠2=∠3=68°.
7.D 在同一平面内,两直线的位置关系是平行或相交,故选项A错误;在平面内,经过直线外一点,有且只有一条直线与这条直线平行,故选项B错误;两条平行线被第三条直线所截,同旁内角互补,故选项C错误;在同一平面内,若直线a⊥b,b⊥c,则直线a∥c.故选D.
8.B ∵∠COA=54°,∴∠BOD=54°.∵EO⊥AB,∴∠EOB=90°,∴∠EOD=90°+54°
=144°.∵OF平分∠EOD,∴∠EOF=∠EOD=72°∴∠FOB=90°-∠EOF=18°.
9.A 两次拐弯后,行驶的方向与原来的方向相同,所以右拐的角度与左拐的角度应相等.
10.C 如图,过点C作CM∥AB,过点D作DN∥EF,因为AB∥EF,所以CM∥DN.因为CM∥AB,所以∠BCM=α,所以∠DCM=90°-α.因为DN∥EF,所以γ=∠EDN,所以∠CDN=β -γ.因为CM∥DN,所以∠DCM=∠CDN,所以90°-α=β -γ,所以α+β -γ=90°.
另解
如图,延长DC交AB于点G,延长CD交EF的延长线于点H.在直角三角形BGC中,∠1=90°-α;在三角形EHD中,∠2=β-γ.因为AB∥EF,所以∠1=∠2,所以90°-α=
β -γ,即α+β -γ=90°.
11.5.42 根据跳远比赛的规则,王明同学的跳远成绩为点P到踏板的距离.他的跳远成绩应该为线段PB的长度,所以他的跳远成绩为5.42米.
12.∠3=∠4(答案不唯一,或∠5=∠B等)
13.151° ∵∠1+∠2=58°,∠1=∠2,∴∠1=×58°=29°,∴∠3=180°-∠1=180°-29°=
151°.
14.70° 如图,由题意可得∠4=∠3=∠1=40°,由折叠可知∠2=∠5==70°.
15.30° 过点E作EF∥CD,∵AB∥CD,∴EF∥AB,∴∠EAB+∠AEF=180°.∵EF
∥CD,∴∠CEF+∠ECD=180°.∵∠EAB=80°,∠ECD=110°,∴∠AEF=100°,∠CEF=70°,∴∠AEC=∠AEF-∠CEF=30°.
16.解:(1)如图. (2分)
(2)OA 线段PC的长度 PH17.解:∵CD∥OB,∠AOB=37°36',∠1=∠3,
∴∠1=∠3=∠AOB=37°36',∠DEB+∠CDE=180°,
∴∠DEB=180°-∠CDE=180°-[180°-(∠1+∠3)]=∠1+∠3=74°72'=75.2°. (8分)
18.解:(1)∠BOD ∠AOE (2分)
(2)∵∠AOC=70°,∴∠DOB=70°. (5分)
∵∠BOE∶∠EOD=2∶3,∴∠BOE=70°×=28°,
∴∠AOE=180°-∠BOE=152°. (8分)
19.解:因为l1∥l2∥l3,
所以∠AMD=∠1=28°,∠DMB=∠2=70°,
所以∠AMB=∠AMD+∠DMB=28°+70°=98°.
因为MC平分∠AMB, 所以∠BMC=∠AMB=×98°=49°,
所以∠DMC=∠DMB -∠BMC=70°-49°=21°. (10分)
20.解:(1)对顶角相等 同位角相等,两直线平行 C 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 (6分)
(2)相等.理由如下: (7分)
∵∠1=∠2,∴DE∥AC,∴∠E=∠EBC.
∵AD∥BE,∴∠A=∠EBC,∴∠A=∠E. (11分)
21.解:(1)过点P作PQ∥AB,∴∠APQ+∠PAB=180°.
∵AB∥CD,∴PQ∥CD,∴∠CPQ+∠PCD=180°. (2分)
∵∠PAB=130°,∠PCD=120°,
∴∠APQ=180°-∠PAB=50°,∠CPQ=180°-∠PCD=60°,
∴∠APC=∠APQ+∠CPQ=50°+60°=110°. (4分)
(2)①∠CPD=∠α+∠β (6分)
如图1,过点P作PE∥AD交ON于点E,∵PE∥AD,AD∥BC,∴∠α=∠DPE,PE
∥BC,∴∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β.
②∠CPD=∠β -∠α或∠CPD=∠α -∠β.理由如下: (8分)
当点P在BA的延长线上时,
如图2,过点P作PH∥AD交ON于点H,
∵PH∥AD,AD∥BC,∴∠α=∠DPH,PH∥BC,∴∠β=∠CPH,
∴∠CPD=∠CPH-∠DPH=∠β-∠α. (10分)
当点P在B,O两点之间时,如图3,过点P作PF∥AD交ON于点F,
∵PF∥AD,AD∥BC,∴∠α=∠DPF,PF∥BC,∴∠β=∠CPF,
∴∠CPD=∠DPF -∠CPF=∠α -∠β. (12分)
图1 图2 图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华师版七年级数学上学期单元测试卷
第5章 相交线与平行线
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.如图,直线AB,CD交于点O,若∠AOC增大50°,则∠BOD ( )
A.不变 B.增大50° C.减少50° D.增大130°
2.如图,直线a,b被直线c所截,则∠1与∠2是 ( )
A.内错角 B.同位角 C.对顶角 D.同旁内角
3.下列画出的直线a与b不一定平行的是 ( )
A B C D
4.如图,俄罗斯方块游戏中,图形A经过平行移动填补空位,则正确的平行移动方式是 ( )
A.先向右平行移动5格,再向下平行移动3格
B.先向右平行移动4格,再向下平行移动5格
C.先向右平行移动3格,再向下平行移动5格
D.先向右平行移动4格,再向下平行移动4格
5.如图,河道l的一侧有A,B两个村庄,现要铺设一条引水管道把河水引向A,B两村,下列四种方案中最节省材料的是 ( )
A B C D
6.如图,将三角板的直角顶点放在两条平行线中的直线AB上,若∠1=22°,则∠2的度数为 ( )
A.78° B.68° C.22° D.60°
7.下列说法正确的是 ( )
A.两直线的位置关系是平行、垂直或相交
B.在平面内,经过直线外一点,有无数条直线与这条直线平行
C.两条直线被第三条直线所截,同旁内角互补
D.在同一平面内,若直线a⊥b,b⊥c,则直线a∥c
8.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,若∠COA=54°,OF平分∠EOD,则∠FOB等于 ( )
A.30° B.18° C.27° D.22°
9.一学员练习驾驶汽车,两次拐弯后,行驶的方向与原来的方向相同,则这两次拐弯的角度可能是 ( )
A.第一次向左拐50°,第二次向右拐50°
B.第一次向右拐50°,第二次向左拐130°
C.第一次向右拐50°,第二次向右拐130°
D.第一次向左拐50°,第二次向左拐130°
10.如图,AB∥EF,∠C=90°,则α,β和γ的关系是 ( )
A.β=α+γ B.α+β+γ=180° C.α+β -γ=90° D.β+γ -α=180°
二、填空题(每小题3分,共15分)
11.如图,是王明同学在跳远比赛中最好的一跳,甲、乙、丙三名同学分别测得PA
=5.55米,PB=5.42米,MA=5.63米,那么王明同学的跳远成绩应该为 米.
12.如图,添加一个条件能得到AB∥CD,则这个条件是 .
13.如图,直线a,b相交,∠1+∠2=58°,则∠3的度数为 .
14.如图,将一个矩形纸片折叠,若∠1=40°,则∠2= .
15.为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB
=80°,∠ECD=110°.求∠AEC的度数.小明在解题过程中,过点E作EF∥CD,则可以得到EF∥AB,根据小明的思路可得∠AEC= .
图1 图2
三、解答题(共55分)
16.(6分)如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为点H.
(2)线段PH的长度是点P到 的距离, 是点C到OB的距离.线段PC,PH,OC这三条线段的大小关系是 (用“<”号连接).
17.(8分)如图,∠AOB的一边OA为平面镜,∠AOB=37°36',在OB上有一点E,从E点射出一束光线(入射光线)经OA上一点D反射,反射光线DC恰好与OB平行(入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠1=∠3),求∠DEB的度数.
18.(8分)如图,直线AB,CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE∶∠EOD=2∶3,求∠AOE的度数.
19.(10分)如图,l1∥l2∥l3,点A,M,B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,
∠2=70°.求∠CMD的度数.
20.(11分)(1)如图1,已知∠1=∠2,∠B=∠C,则AB与CD平行吗
请补全下面的解答过程(填理由或数学式).
解:∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换),
∴CE∥BF( ),
∴∠ =∠BFD( ).
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( ).
(2)如图2,已知AD∥BE,∠1=∠2,则∠A与∠E相等吗 试说明理由.
图1 图2
21.(12分)(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(2)如图2,AD∥BC,点P在射线OM上运动,若∠ADP=∠α,∠BCP=∠β.
①当点P在A,B两点之间运动时,∠CPD,∠α,∠β之间的数量关系为 .
②当点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请写出∠CPD,∠α,
∠β之间的数量关系,并说明理由.
图1 图2
参考答案与解析
1.B 因为∠AOC与∠BOD互为对顶角,所以∠AOC=∠BOD,所以当∠AOC增大50°时,∠BOD也增大50°.故选B.
2.A
3.A 选项A中,直线a与b不一定平行.
4.D
5.C
6.B 如图,根据题意知,∠3=90°-∠1=90°-22°=68°.由平行可知∠2=∠3=68°.
7.D 在同一平面内,两直线的位置关系是平行或相交,故选项A错误;在平面内,经过直线外一点,有且只有一条直线与这条直线平行,故选项B错误;两条平行线被第三条直线所截,同旁内角互补,故选项C错误;在同一平面内,若直线a⊥b,b⊥c,则直线a∥c.故选D.
8.B ∵∠COA=54°,∴∠BOD=54°.∵EO⊥AB,∴∠EOB=90°,∴∠EOD=90°+54°
=144°.∵OF平分∠EOD,∴∠EOF=∠EOD=72°∴∠FOB=90°-∠EOF=18°.
9.A 两次拐弯后,行驶的方向与原来的方向相同,所以右拐的角度与左拐的角度应相等.
10.C 如图,过点C作CM∥AB,过点D作DN∥EF,因为AB∥EF,所以CM∥DN.因为CM∥AB,所以∠BCM=α,所以∠DCM=90°-α.因为DN∥EF,所以γ=∠EDN,所以∠CDN=β -γ.因为CM∥DN,所以∠DCM=∠CDN,所以90°-α=β -γ,所以α+β -γ=90°.
另解
如图,延长DC交AB于点G,延长CD交EF的延长线于点H.在直角三角形BGC中,∠1=90°-α;在三角形EHD中,∠2=β-γ.因为AB∥EF,所以∠1=∠2,所以90°-α=
β -γ,即α+β -γ=90°.
11.5.42 根据跳远比赛的规则,王明同学的跳远成绩为点P到踏板的距离.他的跳远成绩应该为线段PB的长度,所以他的跳远成绩为5.42米.
12.∠3=∠4(答案不唯一,或∠5=∠B等)
13.151° ∵∠1+∠2=58°,∠1=∠2,∴∠1=×58°=29°,∴∠3=180°-∠1=180°-29°=
151°.
14.70° 如图,由题意可得∠4=∠3=∠1=40°,由折叠可知∠2=∠5==70°.
15.30° 过点E作EF∥CD,∵AB∥CD,∴EF∥AB,∴∠EAB+∠AEF=180°.∵EF
∥CD,∴∠CEF+∠ECD=180°.∵∠EAB=80°,∠ECD=110°,∴∠AEF=100°,∠CEF=70°,∴∠AEC=∠AEF-∠CEF=30°.
16.解:(1)如图. (2分)
(2)OA 线段PC的长度 PH
∴∠1=∠3=∠AOB=37°36',∠DEB+∠CDE=180°,
∴∠DEB=180°-∠CDE=180°-[180°-(∠1+∠3)]=∠1+∠3=74°72'=75.2°. (8分)
18.解:(1)∠BOD ∠AOE (2分)
(2)∵∠AOC=70°,∴∠DOB=70°. (5分)
∵∠BOE∶∠EOD=2∶3,∴∠BOE=70°×=28°,
∴∠AOE=180°-∠BOE=152°. (8分)
19.解:因为l1∥l2∥l3,
所以∠AMD=∠1=28°,∠DMB=∠2=70°,
所以∠AMB=∠AMD+∠DMB=28°+70°=98°.
因为MC平分∠AMB, 所以∠BMC=∠AMB=×98°=49°,
所以∠DMC=∠DMB -∠BMC=70°-49°=21°. (10分)
20.解:(1)对顶角相等 同位角相等,两直线平行 C 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 (6分)
(2)相等.理由如下: (7分)
∵∠1=∠2,∴DE∥AC,∴∠E=∠EBC.
∵AD∥BE,∴∠A=∠EBC,∴∠A=∠E. (11分)
21.解:(1)过点P作PQ∥AB,∴∠APQ+∠PAB=180°.
∵AB∥CD,∴PQ∥CD,∴∠CPQ+∠PCD=180°. (2分)
∵∠PAB=130°,∠PCD=120°,
∴∠APQ=180°-∠PAB=50°,∠CPQ=180°-∠PCD=60°,
∴∠APC=∠APQ+∠CPQ=50°+60°=110°. (4分)
(2)①∠CPD=∠α+∠β (6分)
如图1,过点P作PE∥AD交ON于点E,∵PE∥AD,AD∥BC,∴∠α=∠DPE,PE
∥BC,∴∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β.
②∠CPD=∠β -∠α或∠CPD=∠α -∠β.理由如下: (8分)
当点P在BA的延长线上时,
如图2,过点P作PH∥AD交ON于点H,
∵PH∥AD,AD∥BC,∴∠α=∠DPH,PH∥BC,∴∠β=∠CPH,
∴∠CPD=∠CPH-∠DPH=∠β-∠α. (10分)
当点P在B,O两点之间时,如图3,过点P作PF∥AD交ON于点F,
∵PF∥AD,AD∥BC,∴∠α=∠DPF,PF∥BC,∴∠β=∠CPF,
∴∠CPD=∠DPF -∠CPF=∠α -∠β. (12分)
图1 图2 图3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
