第4单元 几何图形初步测试卷(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版七年级数学上学期单元测试卷
第四章 几何图形初步
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
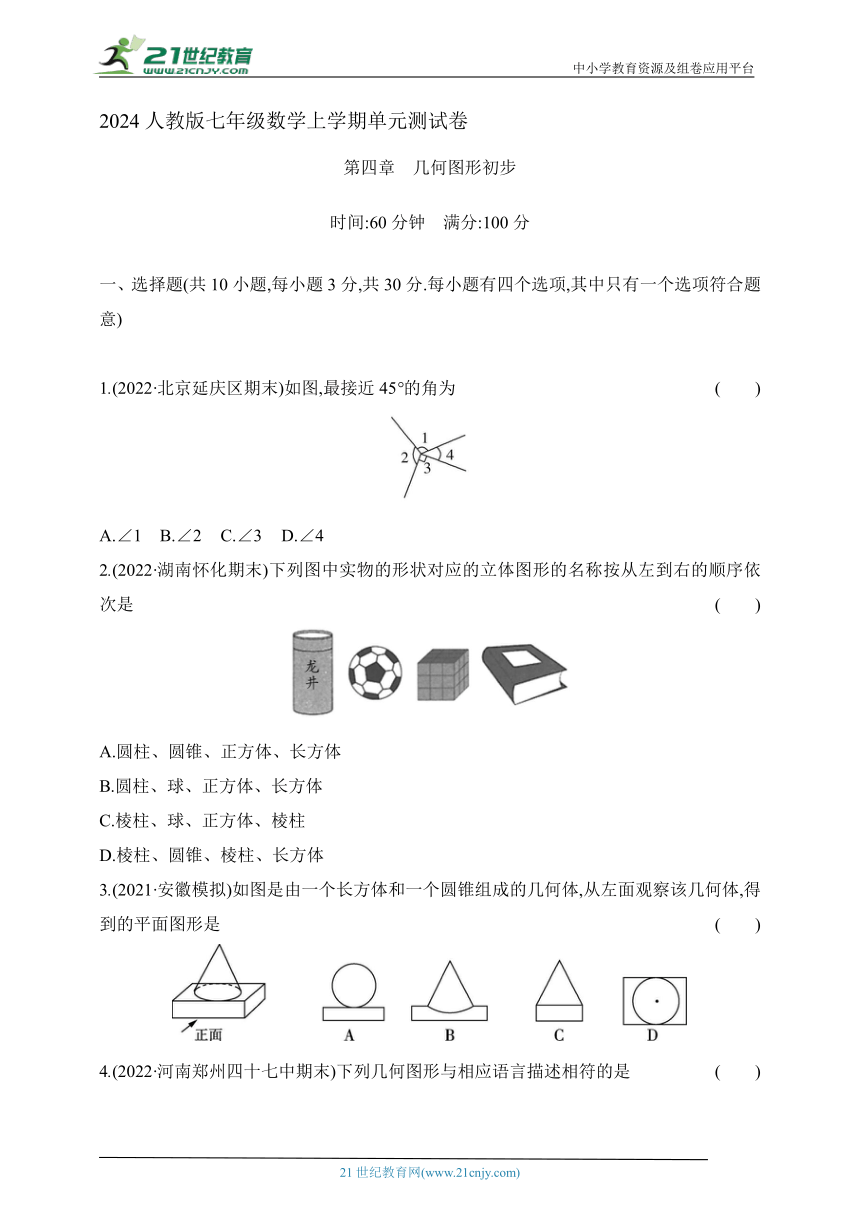
1.(2022·北京延庆区期末)如图,最接近45°的角为 ( )
A.∠1 B.∠2 C.∠3 D.∠4
2.(2022·湖南怀化期末)下列图中实物的形状对应的立体图形的名称按从左到右的顺序依次是 ( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
3.(2021·安徽模拟)如图是由一个长方体和一个圆锥组成的几何体,从左面观察该几何体,得到的平面图形是 ( )
4.(2022·河南郑州四十七中期末)下列几何图形与相应语言描述相符的是 ( )
A.如图(1),延长线段BA至点C
B.如图(2),射线BC经过点A
C.如图(3),直线a和直线b相交于点A
D.如图(4),射线CD和线段AB没有交点
5.(2022·浙江嘉兴期末)如图,已知AB=12,点C在线段AB上,BC=AB,点D是线段AB的中点,则线段CD的长度为 ( )
A.2 B.3 C.4 D.6
6.(2022·重庆南川区期末)如图是一个正方体的平面展开图,则该正方体可能是 ( )
A B C D
7.(2022·北京丰台区期末)只借助一副三角尺拼摆,不能画出下列哪个度数的角 ( )
A.15° B.65° C.75° D.135°
8.(2021·安徽马鞍山期末)若∠α与∠β互补(∠α<∠β),则∠α与(∠β-∠α)的关系是 ( )
A.互补 B.互余
C.和为45° D.和为22.5°
9.(2022·江苏无锡锡山区期末)如图,C,D是线段AB上两点,若CD=3AD-2BC,则AC与BD的数量关系是 ( )
A.AC=BD B.2AC=BD
C.3AC=2BD D.4AC=3BD
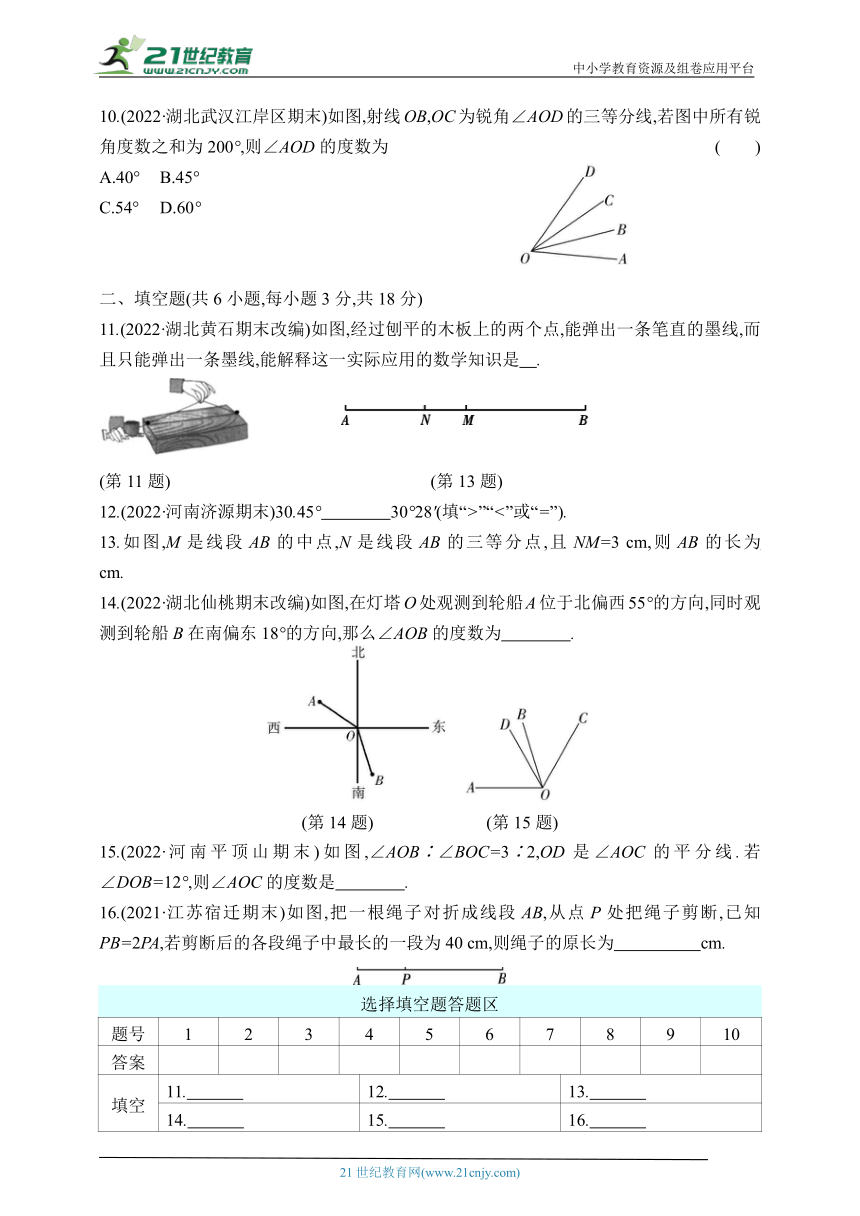
10.(2022·湖北武汉江岸区期末)如图,射线OB,OC为锐角∠AOD的三等分线,若图中所有锐角度数之和为200°,则∠AOD的度数为 ( )
A.40° B.45°
C.54° D.60°
二、填空题(共6小题,每小题3分,共18分)
11.(2022·湖北黄石期末改编)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
(第11题) (第13题)
12.(2022·河南济源期末)30.45° 30°28'(填“>”“<”或“=”).
13.如图,M是线段AB的中点,N是线段AB的三等分点,且NM=3 cm,则AB的长为 cm.
14.(2022·湖北仙桃期末改编)如图,在灯塔O处观测到轮船A位于北偏西55°的方向,同时观测到轮船B在南偏东18°的方向,那么∠AOB的度数为 .
(第14题) (第15题)
15.(2022·河南平顶山期末)如图,∠AOB∶∠BOC=3∶2,OD是∠AOC的平分线.若∠DOB=12°,则∠AOC的度数是 .
16.(2021·江苏宿迁期末)如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知PB=2PA,若剪断后的各段绳子中最长的一段为40 cm,则绳子的原长为 cm.
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(6分)(2021·北京东城区期末)补全解题过程:如图,已知线段AB=6,延长AB至点C,使BC=2AB,点P,Q分别是线段AC和AB的中点,求PQ的长.
解:因为BC=2AB,AB=6,
所以BC=2×6=12,
所以AC= + =6+12=18.
因为点P,Q分别是线段AC和AB的中点,
所以AP= =×18=9,
AQ= =×6=3,
所以PQ= - =9-3=6.
18.(6分)如图,已知线段a,b.用圆规在射线OA上画一条线段OB,使OB=2a-b.(保留作图痕迹)
19.(8分)(2022·河南周口期末改编)如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)判断OE是否平分∠BOC,并说明理由;
(2)∠BOE的余角是 .
20.(10分)(2022·吉林延边州期末)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示.
(1)A对面的字母是 ,E对面的字母是 ,C对面的字母是 ;
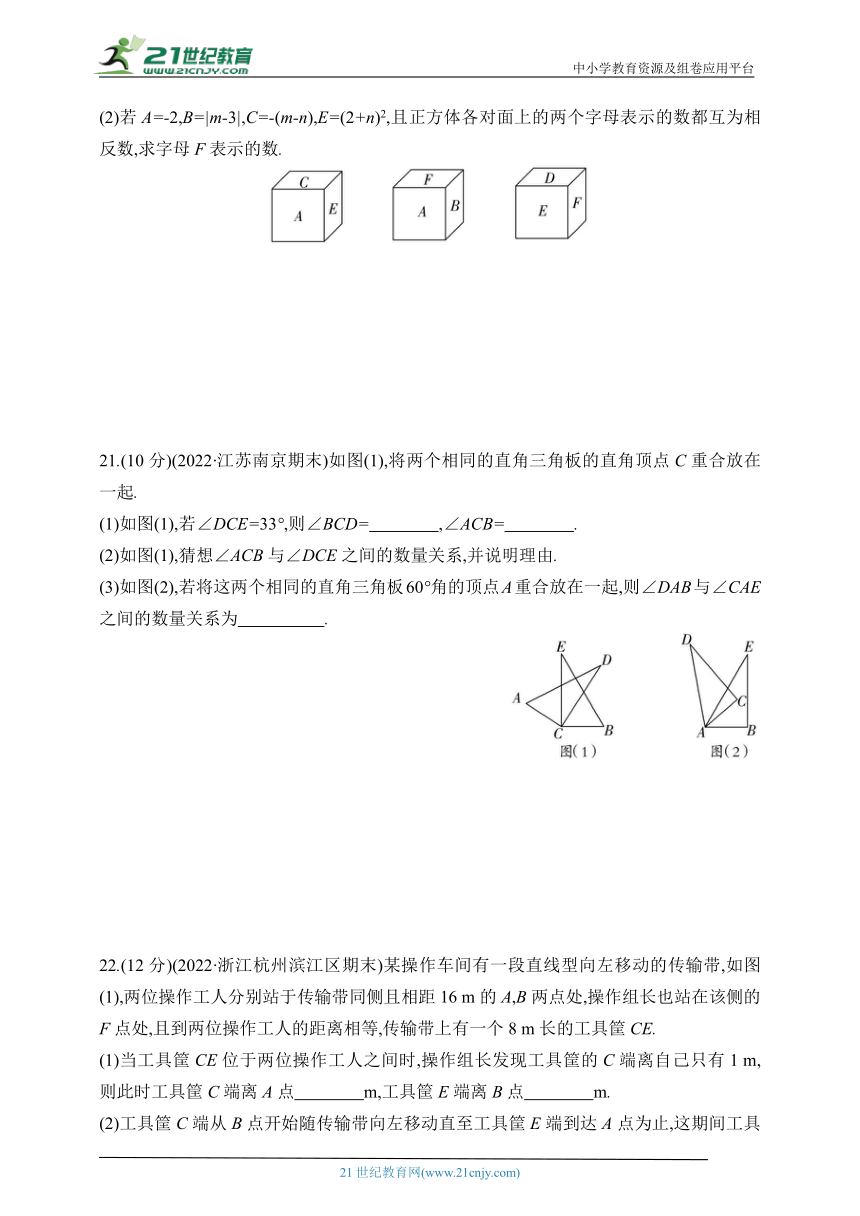
(2)若A=-2,B=|m-3|,C=-(m-n),E=(2+n)2,且正方体各对面上的两个字母表示的数都互为相反数,求字母F表示的数.
21.(10分)(2022·江苏南京期末)如图(1),将两个相同的直角三角板的直角顶点C重合放在一起.
(1)如图(1),若∠DCE=33°,则∠BCD= ,∠ACB= .
(2)如图(1),猜想∠ACB与∠DCE之间的数量关系,并说明理由.
(3)如图(2),若将这两个相同的直角三角板60°角的顶点A重合放在一起,则∠DAB与∠CAE之间的数量关系为 .
22.(12分)(2022·浙江杭州滨江区期末)某操作车间有一段直线型向左移动的传输带,如图(1),两位操作工人分别站于传输带同侧且相距16 m的A,B两点处,操作组长也站在该侧的F点处,且到两位操作工人的距离相等,传输带上有一个8 m长的工具筐CE.
(1)当工具筐CE位于两位操作工人之间时,操作组长发现工具筐的C端离自己只有1 m,则此时工具筐C端离A点 m,工具筐E端离B点 m.
(2)工具筐C端从B点开始随传输带向左移动直至工具筐E端到达A点为止,这期间工具筐E端到B点的距离BE和工具筐E端到F点的距离EF之间存在怎样的数量关系 请说明理由.
第四章 几何图形初步·B卷
1 2 3 4 5 6 7 8 9 10
D B C C A D B B C D
11.两点确定一条直线 12.< 13.18
14.143° 15.120° 16.60或120
1.D
2.B
3.C 从左面看,底层是一个长方形,上层是一个三角形,故选C.
4.C (排除法)如题图(1),延长线段BA至点C,几何图形与相应语言描述不相符;如题图(2),射线BC不经过点A;如题图(4),因为射线可以延伸,所以射线CD和线段AB有交点.
5.A 因为AB=12,BC=AB,所以BC=4.因为点D是线段AB的中点,所以BD=AB=6,所以CD=BD-BC=2.
6.D (排除法)由正方体的展开图可知,两个圆所在面是相对的面,故选项A,B不合题意;空心圆所在面的一边与含阴影的直角三角形的直角边重合,故选项C不合题意.
7.B 由题意可得,一副三角尺中的角度分别为30°,60°,45°,90°.因为45°-30°=15°,45°+30°=75°,45°+90°=135°,所以用一副三角尺拼摆,不能画出65°的角.故选B.
8.B 因为∠α与∠β互补(∠α<∠β),所以∠α+∠β=180°,所以∠α+(∠β-∠α)=(∠α+∠β)=90°,所以∠α与(∠β-∠α)的关系是互余.故选B.
9.C 因为CD=3AD-2BC,所以CD=3(AC+CD)-2(BD+CD)=3AC+3CD-2BD-2CD=3AC-2BD+CD,所以3AC=2BD.故选C.
10.D 因为射线OB,OC为锐角∠AOD的三等分线,所以∠AOB=∠BOC=∠COD.设∠AOB=∠BOC=∠COD=x,所以∠AOB+∠BOC+∠COD+∠AOC+∠AOD+∠BOD=x+x+x+2x+3x+2x=10x=200°,解得x=20°,所以∠AOD=3x=60°.
一题多解
因为射线OB,OC为锐角∠AOD的三等分线,所以∠AOB=∠BOC=∠COD,所以∠AOC=∠BOD=2∠BOC=2∠AOB,∠AOD=3∠AOB,所以∠AOB+∠BOC+∠COD+∠AOC+∠BOD+∠AOD=∠AOB+∠AOB+∠AOB+2∠AOB+2∠AOB+3∠AOB=10∠AOB=200°,解得∠AOB=20°,所以∠AOD=3∠AOB=60°.
11.两点确定一条直线
12.< 因为1°=60',所以0.45°=27',所以30.45°=30°+0.45°=30°27',所以30°27'<30°28',所以30.45°<30°28'.
13.18 因为M是线段AB的中点,所以AM=AB.因为N是线段AB的三等分点,所以AN=AB.因为MN=AM-AN=AB-AB=3,所以AB=18 cm.
14.143° 如图,由题意得∠1=55°,∠2=18°,所以∠3=90°-55°=35°,所以∠AOB=35°+90°+18°=143°.
15.120° 设∠AOB=3x,∠BOC=2x,则∠AOC=∠AOB+∠BOC=5x.因为OD是∠AOC的平分线,所以∠AOD=∠AOC=x,所以∠DOB=∠AOB-∠AOD=3x-x=x=12°,解得x=24°,所以∠AOC=5x=120°.
16.60或120 (分类讨论思想)设AP=x cm,则BP=2x cm,绳子的原长为6x cm.①当含有线段AP的绳子最长时,x+x=40,解得x=20,即绳子的原长为6×20=120(cm);②当含有线段BP的绳子最长时,2x+2x=40,解得x=10,即绳子的原长为6×10=60(cm).综上,绳长的原长为60 cm或120 cm.
17.【参考答案】因为BC=2AB,AB=6,
所以BC=2×6=12,
所以AC=AB+BC=6+12=18. (2分)
因为点P,Q分别是线段AC和AB的中点,
所以AP=AC=×18=9, (3分)
AQ=AB=×6=3, (4分)
所以PQ=AP-AQ=9-3=6. (6分)
18.【参考答案】如图,用圆规在射线OA上截取OC=a,CD=a,
在线段DO上截取DB=b,
则OB=OD-BD=2a-b,线段OB即为所求.
(6分)
19.【参考答案】(1)OE平分∠BOC. (2分)
理由如下:
因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=∠AOC=25°.
因为∠DOE=90°,
所以∠COE=∠DOE-∠DOC=90°-25°=65°,
所以∠BOE=180°-∠AOC-∠COE=180°-50°-65°=65°,
所以∠COE=∠BOE,
所以OE平分∠BOC. (6分)
(2)∠DOC和∠DOA (8分)
解法提示:因为∠BOE=65°,∠DOA=∠DOC=25°,
所以∠BOE+∠DOA=90°,∠BOE+∠DOC=90°,
所以∠BOE的余角是∠DOC和∠DOA.
20.【参考答案】(1)D B F (6分)
解法提示:由题图可知,A相邻的字母有C,E,B,F,所以A对面的字母是D,与E相邻的字母有C,A,D,F,所以E对面的字母是B,所以C对面的字母是F.
(2)因为正方体各对面上的两个字母表示的数都互为相反数,
所以|m-3|+(2+n)2=0,
解得m=3,n=-2, (8分)
所以C=-(m-n)=-5,
所以字母F表示的数为5. (10分)
21.【参考答案】(1)57° 147° (4分)
解法提示:由题意得∠ACD=∠BCE=90°,
因为∠DCE=33°,
所以∠BCD=90°-∠DCE=57°,
所以∠ACB=∠ACD+∠BCD=90°+57°=147°.
(2)∠ACB=180°-∠DCE. (5分)
理由如下:
因为∠ACD=90°,∠BCD=90°-∠DCE,
所以∠ACB=∠ACD+∠BCD
=90°+90°-∠DCE
=180°-∠DCE. (8分)
(3)∠DAB=120°-∠CAE (10分)
解法提示:因为∠DAC=60°,
∠BAC=∠BAE-∠CAE=60°-∠CAE,
所以∠DAB=∠DAC+∠BAC
=60°+60°-∠CAE
=120°-∠CAE.
22.【参考答案】(1)7 1 (4分)
解法提示:由题意得AB=16 m,
因为操作组长到两位操作工人的距离相等,
所以AF=BF=8 m.
因为CE=8 m,CF=1 m,
所以AC=8-1=7(m),BE=8-7=1(m).
(2)EF-BE=8,EF+BE=8或BE-EF=8.
理由如下:
①当工具筐C端在线段BF上时,如图(1),
易得EF-BE=BF=8. (6分)
②当工具筐C端在线段AF上时,如图(2),
易得EF+BE=BF=8. (9分)
③当工具筐C端在点A左侧时,如图(3),
易得BE-EF=BF=8.
综上,EF-BE=8,EF+BE=8或BE-EF=8. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版七年级数学上学期单元测试卷
第四章 几何图形初步
时间:60分钟 满分:100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2022·北京延庆区期末)如图,最接近45°的角为 ( )
A.∠1 B.∠2 C.∠3 D.∠4
2.(2022·湖南怀化期末)下列图中实物的形状对应的立体图形的名称按从左到右的顺序依次是 ( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
3.(2021·安徽模拟)如图是由一个长方体和一个圆锥组成的几何体,从左面观察该几何体,得到的平面图形是 ( )
4.(2022·河南郑州四十七中期末)下列几何图形与相应语言描述相符的是 ( )
A.如图(1),延长线段BA至点C
B.如图(2),射线BC经过点A
C.如图(3),直线a和直线b相交于点A
D.如图(4),射线CD和线段AB没有交点
5.(2022·浙江嘉兴期末)如图,已知AB=12,点C在线段AB上,BC=AB,点D是线段AB的中点,则线段CD的长度为 ( )
A.2 B.3 C.4 D.6
6.(2022·重庆南川区期末)如图是一个正方体的平面展开图,则该正方体可能是 ( )
A B C D
7.(2022·北京丰台区期末)只借助一副三角尺拼摆,不能画出下列哪个度数的角 ( )
A.15° B.65° C.75° D.135°
8.(2021·安徽马鞍山期末)若∠α与∠β互补(∠α<∠β),则∠α与(∠β-∠α)的关系是 ( )
A.互补 B.互余
C.和为45° D.和为22.5°
9.(2022·江苏无锡锡山区期末)如图,C,D是线段AB上两点,若CD=3AD-2BC,则AC与BD的数量关系是 ( )
A.AC=BD B.2AC=BD
C.3AC=2BD D.4AC=3BD
10.(2022·湖北武汉江岸区期末)如图,射线OB,OC为锐角∠AOD的三等分线,若图中所有锐角度数之和为200°,则∠AOD的度数为 ( )
A.40° B.45°
C.54° D.60°
二、填空题(共6小题,每小题3分,共18分)
11.(2022·湖北黄石期末改编)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是 .
(第11题) (第13题)
12.(2022·河南济源期末)30.45° 30°28'(填“>”“<”或“=”).
13.如图,M是线段AB的中点,N是线段AB的三等分点,且NM=3 cm,则AB的长为 cm.
14.(2022·湖北仙桃期末改编)如图,在灯塔O处观测到轮船A位于北偏西55°的方向,同时观测到轮船B在南偏东18°的方向,那么∠AOB的度数为 .
(第14题) (第15题)
15.(2022·河南平顶山期末)如图,∠AOB∶∠BOC=3∶2,OD是∠AOC的平分线.若∠DOB=12°,则∠AOC的度数是 .
16.(2021·江苏宿迁期末)如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知PB=2PA,若剪断后的各段绳子中最长的一段为40 cm,则绳子的原长为 cm.
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.
三、解答题(共6小题,共52分)
17.(6分)(2021·北京东城区期末)补全解题过程:如图,已知线段AB=6,延长AB至点C,使BC=2AB,点P,Q分别是线段AC和AB的中点,求PQ的长.
解:因为BC=2AB,AB=6,
所以BC=2×6=12,
所以AC= + =6+12=18.
因为点P,Q分别是线段AC和AB的中点,
所以AP= =×18=9,
AQ= =×6=3,
所以PQ= - =9-3=6.
18.(6分)如图,已知线段a,b.用圆规在射线OA上画一条线段OB,使OB=2a-b.(保留作图痕迹)
19.(8分)(2022·河南周口期末改编)如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)判断OE是否平分∠BOC,并说明理由;
(2)∠BOE的余角是 .
20.(10分)(2022·吉林延边州期末)一个正方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示.
(1)A对面的字母是 ,E对面的字母是 ,C对面的字母是 ;
(2)若A=-2,B=|m-3|,C=-(m-n),E=(2+n)2,且正方体各对面上的两个字母表示的数都互为相反数,求字母F表示的数.
21.(10分)(2022·江苏南京期末)如图(1),将两个相同的直角三角板的直角顶点C重合放在一起.
(1)如图(1),若∠DCE=33°,则∠BCD= ,∠ACB= .
(2)如图(1),猜想∠ACB与∠DCE之间的数量关系,并说明理由.
(3)如图(2),若将这两个相同的直角三角板60°角的顶点A重合放在一起,则∠DAB与∠CAE之间的数量关系为 .
22.(12分)(2022·浙江杭州滨江区期末)某操作车间有一段直线型向左移动的传输带,如图(1),两位操作工人分别站于传输带同侧且相距16 m的A,B两点处,操作组长也站在该侧的F点处,且到两位操作工人的距离相等,传输带上有一个8 m长的工具筐CE.
(1)当工具筐CE位于两位操作工人之间时,操作组长发现工具筐的C端离自己只有1 m,则此时工具筐C端离A点 m,工具筐E端离B点 m.
(2)工具筐C端从B点开始随传输带向左移动直至工具筐E端到达A点为止,这期间工具筐E端到B点的距离BE和工具筐E端到F点的距离EF之间存在怎样的数量关系 请说明理由.
第四章 几何图形初步·B卷
1 2 3 4 5 6 7 8 9 10
D B C C A D B B C D
11.两点确定一条直线 12.< 13.18
14.143° 15.120° 16.60或120
1.D
2.B
3.C 从左面看,底层是一个长方形,上层是一个三角形,故选C.
4.C (排除法)如题图(1),延长线段BA至点C,几何图形与相应语言描述不相符;如题图(2),射线BC不经过点A;如题图(4),因为射线可以延伸,所以射线CD和线段AB有交点.
5.A 因为AB=12,BC=AB,所以BC=4.因为点D是线段AB的中点,所以BD=AB=6,所以CD=BD-BC=2.
6.D (排除法)由正方体的展开图可知,两个圆所在面是相对的面,故选项A,B不合题意;空心圆所在面的一边与含阴影的直角三角形的直角边重合,故选项C不合题意.
7.B 由题意可得,一副三角尺中的角度分别为30°,60°,45°,90°.因为45°-30°=15°,45°+30°=75°,45°+90°=135°,所以用一副三角尺拼摆,不能画出65°的角.故选B.
8.B 因为∠α与∠β互补(∠α<∠β),所以∠α+∠β=180°,所以∠α+(∠β-∠α)=(∠α+∠β)=90°,所以∠α与(∠β-∠α)的关系是互余.故选B.
9.C 因为CD=3AD-2BC,所以CD=3(AC+CD)-2(BD+CD)=3AC+3CD-2BD-2CD=3AC-2BD+CD,所以3AC=2BD.故选C.
10.D 因为射线OB,OC为锐角∠AOD的三等分线,所以∠AOB=∠BOC=∠COD.设∠AOB=∠BOC=∠COD=x,所以∠AOB+∠BOC+∠COD+∠AOC+∠AOD+∠BOD=x+x+x+2x+3x+2x=10x=200°,解得x=20°,所以∠AOD=3x=60°.
一题多解
因为射线OB,OC为锐角∠AOD的三等分线,所以∠AOB=∠BOC=∠COD,所以∠AOC=∠BOD=2∠BOC=2∠AOB,∠AOD=3∠AOB,所以∠AOB+∠BOC+∠COD+∠AOC+∠BOD+∠AOD=∠AOB+∠AOB+∠AOB+2∠AOB+2∠AOB+3∠AOB=10∠AOB=200°,解得∠AOB=20°,所以∠AOD=3∠AOB=60°.
11.两点确定一条直线
12.< 因为1°=60',所以0.45°=27',所以30.45°=30°+0.45°=30°27',所以30°27'<30°28',所以30.45°<30°28'.
13.18 因为M是线段AB的中点,所以AM=AB.因为N是线段AB的三等分点,所以AN=AB.因为MN=AM-AN=AB-AB=3,所以AB=18 cm.
14.143° 如图,由题意得∠1=55°,∠2=18°,所以∠3=90°-55°=35°,所以∠AOB=35°+90°+18°=143°.
15.120° 设∠AOB=3x,∠BOC=2x,则∠AOC=∠AOB+∠BOC=5x.因为OD是∠AOC的平分线,所以∠AOD=∠AOC=x,所以∠DOB=∠AOB-∠AOD=3x-x=x=12°,解得x=24°,所以∠AOC=5x=120°.
16.60或120 (分类讨论思想)设AP=x cm,则BP=2x cm,绳子的原长为6x cm.①当含有线段AP的绳子最长时,x+x=40,解得x=20,即绳子的原长为6×20=120(cm);②当含有线段BP的绳子最长时,2x+2x=40,解得x=10,即绳子的原长为6×10=60(cm).综上,绳长的原长为60 cm或120 cm.
17.【参考答案】因为BC=2AB,AB=6,
所以BC=2×6=12,
所以AC=AB+BC=6+12=18. (2分)
因为点P,Q分别是线段AC和AB的中点,
所以AP=AC=×18=9, (3分)
AQ=AB=×6=3, (4分)
所以PQ=AP-AQ=9-3=6. (6分)
18.【参考答案】如图,用圆规在射线OA上截取OC=a,CD=a,
在线段DO上截取DB=b,
则OB=OD-BD=2a-b,线段OB即为所求.
(6分)
19.【参考答案】(1)OE平分∠BOC. (2分)
理由如下:
因为∠AOC=50°,OD平分∠AOC,
所以∠DOC=∠AOC=25°.
因为∠DOE=90°,
所以∠COE=∠DOE-∠DOC=90°-25°=65°,
所以∠BOE=180°-∠AOC-∠COE=180°-50°-65°=65°,
所以∠COE=∠BOE,
所以OE平分∠BOC. (6分)
(2)∠DOC和∠DOA (8分)
解法提示:因为∠BOE=65°,∠DOA=∠DOC=25°,
所以∠BOE+∠DOA=90°,∠BOE+∠DOC=90°,
所以∠BOE的余角是∠DOC和∠DOA.
20.【参考答案】(1)D B F (6分)
解法提示:由题图可知,A相邻的字母有C,E,B,F,所以A对面的字母是D,与E相邻的字母有C,A,D,F,所以E对面的字母是B,所以C对面的字母是F.
(2)因为正方体各对面上的两个字母表示的数都互为相反数,
所以|m-3|+(2+n)2=0,
解得m=3,n=-2, (8分)
所以C=-(m-n)=-5,
所以字母F表示的数为5. (10分)
21.【参考答案】(1)57° 147° (4分)
解法提示:由题意得∠ACD=∠BCE=90°,
因为∠DCE=33°,
所以∠BCD=90°-∠DCE=57°,
所以∠ACB=∠ACD+∠BCD=90°+57°=147°.
(2)∠ACB=180°-∠DCE. (5分)
理由如下:
因为∠ACD=90°,∠BCD=90°-∠DCE,
所以∠ACB=∠ACD+∠BCD
=90°+90°-∠DCE
=180°-∠DCE. (8分)
(3)∠DAB=120°-∠CAE (10分)
解法提示:因为∠DAC=60°,
∠BAC=∠BAE-∠CAE=60°-∠CAE,
所以∠DAB=∠DAC+∠BAC
=60°+60°-∠CAE
=120°-∠CAE.
22.【参考答案】(1)7 1 (4分)
解法提示:由题意得AB=16 m,
因为操作组长到两位操作工人的距离相等,
所以AF=BF=8 m.
因为CE=8 m,CF=1 m,
所以AC=8-1=7(m),BE=8-7=1(m).
(2)EF-BE=8,EF+BE=8或BE-EF=8.
理由如下:
①当工具筐C端在线段BF上时,如图(1),
易得EF-BE=BF=8. (6分)
②当工具筐C端在线段AF上时,如图(2),
易得EF+BE=BF=8. (9分)
③当工具筐C端在点A左侧时,如图(3),
易得BE-EF=BF=8.
综上,EF-BE=8,EF+BE=8或BE-EF=8. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
