第十八章 函数及其图象复习(浙江省台州市)
文档属性
| 名称 | 第十八章 函数及其图象复习(浙江省台州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 555.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-06 00:00:00 | ||
图片预览







文档简介
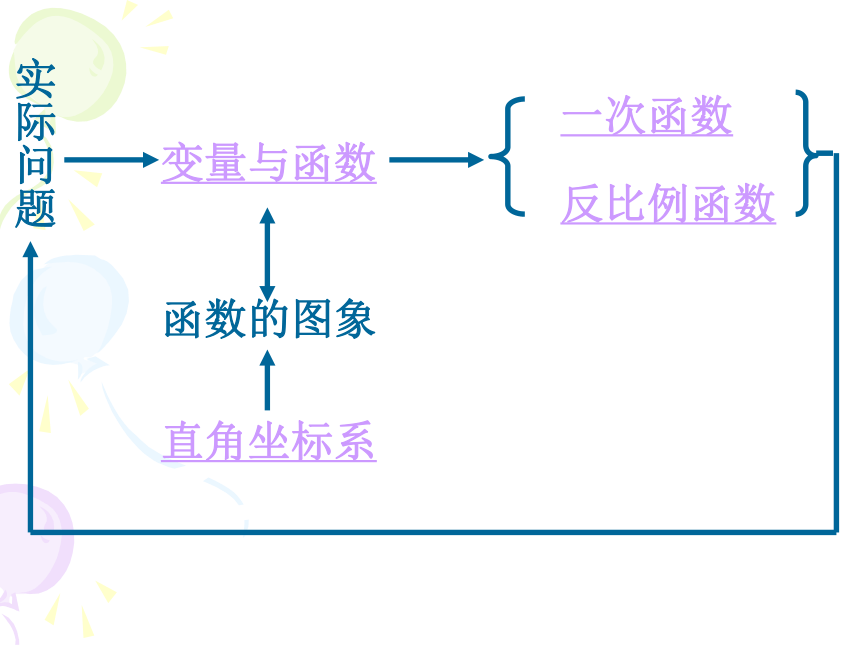
课件31张PPT。第十八章
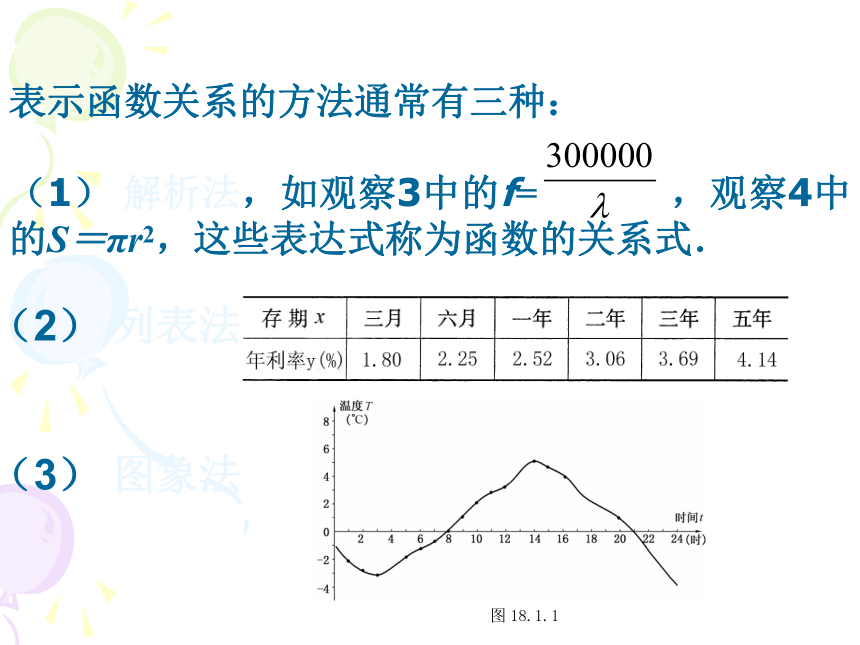
函数及其图象复习课实际问题变量与函数一次函数反比例函数函数的图象直角坐标系在某一变化过程中,可以取不同数值的量,叫做变量 。如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量y是因变量此时也称y是x的函数 。表示函数关系的方法通常有三种:
?
(1) 解析法,如观察3中的f= ,观察4中的S=πr2,这些表达式称为函数的关系式. ?(2) 列表法??(3) 图象法求自变量的取值范围
(1)分母≠0
(2)开偶次方时,被开方数≥0函数相同的条件:(1)函数表达式相同;
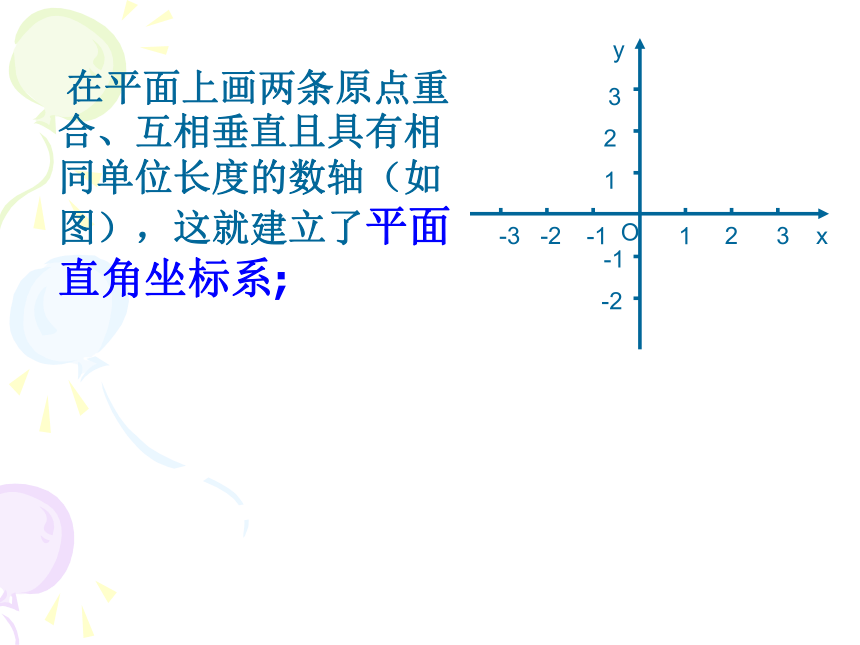
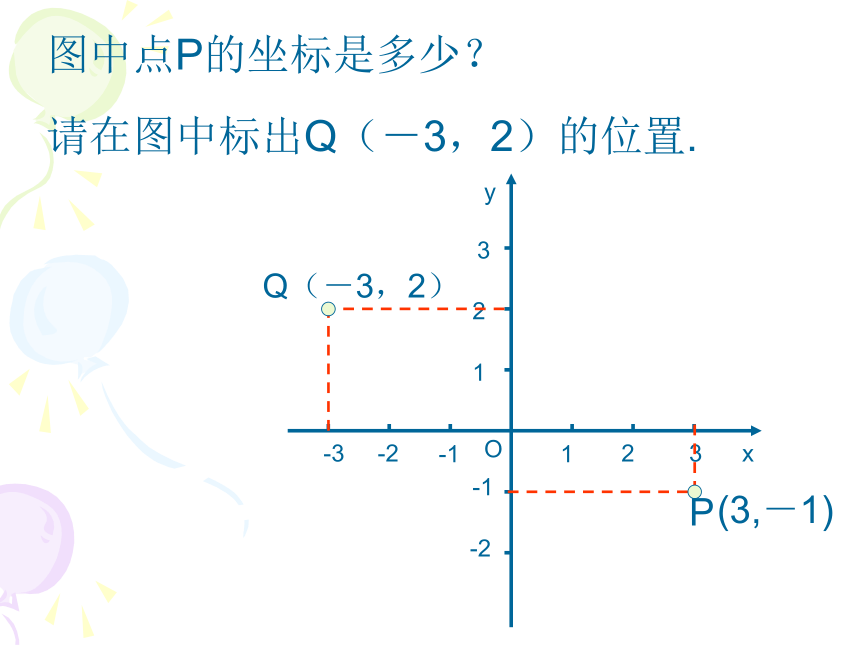
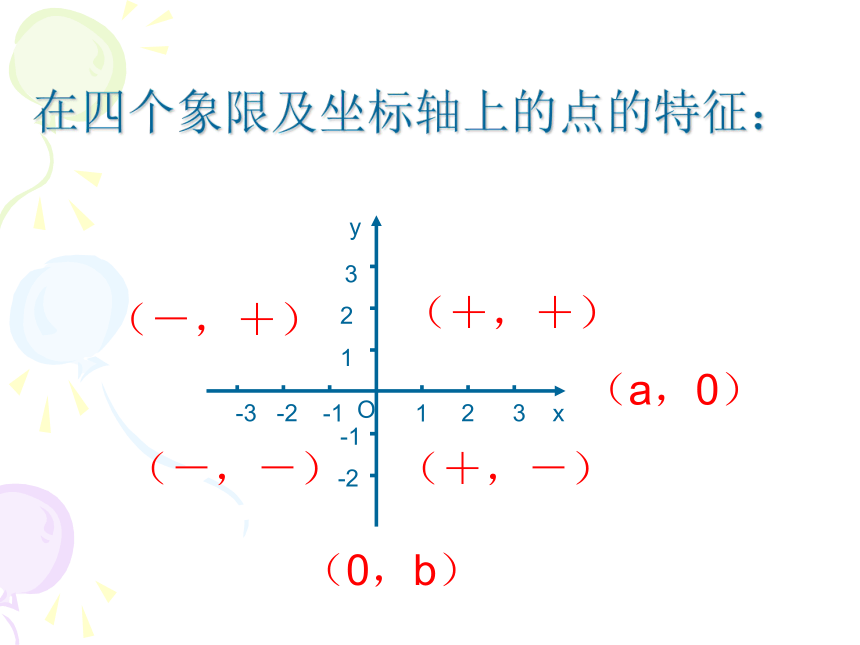
(2)自变量的取值范围相同。 在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系;P(3,-1)图中点P的坐标是多少?请在图中标出Q(-3,2)的位置.Q(-3,2)在四个象限及坐标轴上的点的特征:(+,+)(-,+)(-,-)(+,-)(a,0)(0,b)若点P(a,b)在第四象限,则点
M(a-b,b-a)在第( )象限。
点P(3-m,m)是第二象限内的点,则m的取值范围为( )(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;(2)关于y轴对称的两点:横坐标互为相反数,纵坐标相同;(3)关于原点对称的两点:横坐标坐标互为相反数,纵坐标也坐标互为相反数.关于x轴、y轴、坐标原点对称的点的特征:若点P(a,-2),Q(3,b)关于原点对称,则a-b=( )
一次函数知识要点:1、一次函数的概念:函数y=_______(k、b为常数,k____)叫做一次函数。当b___时,函数y=____(k____)叫做正比例函数。kx +b≠0=0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0已知函数 , 问
(1)当m为何值时,它是一次函数?
(2)当m为何值时,它是正比例函数?概括: (1)y=kx+b,当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;概括: (2)y=kx+b,当k<0时,y随x的增大而减小,这时函数的图象从左到右下降;4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;
y随x的增大而 ____。
⑵当k<0时,图象过______象限;
y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:直线y=5x-10过点( ,0)、(0, )
直线y+2x=1与x轴的交点为 ,与y轴的交点为 . 2-10(0.5,0)(0,1)反比例函数的定义一般地,形如
的函数叫做反比例函数.其中k叫做比例系数.反比例函数的变形形式:1、若双曲线 经过点A(m,-2m), 则m 的值为 . 2、若反比例函数 的图象上有两点 A.正数 B.负数 C.非正数 D.非负数 ±2A3. 当m为何值时,函数 是反比例函数,并求出其函数解析式. 1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,曲线至左向右下降,y随x的增大而减小;2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,曲线至左向右上升, y随x的增大而增大。0位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别在同一坐标系中,正比例函数 y=(m-1)x与反比例函数 的图象大致位置不可能是 ( )利用待定系数法求函数的关系式1、按题目条件设函数的一般表达式
2、代入已知条件,得到方程组
3、解这个方程组
4、写出所求表达式
如果双曲线 经过点(-2,3),那么此双曲线也经过点( )
A.(-2,-3) B.(3,2)
C.(3,-2) D.(-3,-2)已知一次函数的图象如下图,
(1)求出这个函数的关系式;
(2)求△ABO的面积AB利用函数图象解方程组(1,1)利用函数图象解不等式 当x为何值时,(1,1)利用函数图象分析函数类型
(1)画出函数图象,分析函数的类型
(2)设相应的函数关系式
(3)求出未知系数某市出租车公司规定:出租车收费与行驶路程关系如图所示。如果小明姥姥乘出租车去小明家花了22元,那么小明姥姥乘车路程有___千米。
?
(1) 解析法,如观察3中的f= ,观察4中的S=πr2,这些表达式称为函数的关系式. ?(2) 列表法??(3) 图象法求自变量的取值范围
(1)分母≠0
(2)开偶次方时,被开方数≥0函数相同的条件:(1)函数表达式相同;
(2)自变量的取值范围相同。 在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系;P(3,-1)图中点P的坐标是多少?请在图中标出Q(-3,2)的位置.Q(-3,2)在四个象限及坐标轴上的点的特征:(+,+)(-,+)(-,-)(+,-)(a,0)(0,b)若点P(a,b)在第四象限,则点
M(a-b,b-a)在第( )象限。
点P(3-m,m)是第二象限内的点,则m的取值范围为( )(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;(2)关于y轴对称的两点:横坐标互为相反数,纵坐标相同;(3)关于原点对称的两点:横坐标坐标互为相反数,纵坐标也坐标互为相反数.关于x轴、y轴、坐标原点对称的点的特征:若点P(a,-2),Q(3,b)关于原点对称,则a-b=( )
一次函数知识要点:1、一次函数的概念:函数y=_______(k、b为常数,k____)叫做一次函数。当b___时,函数y=____(k____)叫做正比例函数。kx +b≠0=0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0已知函数 , 问
(1)当m为何值时,它是一次函数?
(2)当m为何值时,它是正比例函数?概括: (1)y=kx+b,当k>0时,y随x的增大而增大,这时函数的图象从左到右上升;概括: (2)y=kx+b,当k<0时,y随x的增大而减小,这时函数的图象从左到右下降;4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;
y随x的增大而 ____。
⑵当k<0时,图象过______象限;
y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:直线y=5x-10过点( ,0)、(0, )
直线y+2x=1与x轴的交点为 ,与y轴的交点为 . 2-10(0.5,0)(0,1)反比例函数的定义一般地,形如
的函数叫做反比例函数.其中k叫做比例系数.反比例函数的变形形式:1、若双曲线 经过点A(m,-2m), 则m 的值为 . 2、若反比例函数 的图象上有两点 A.正数 B.负数 C.非正数 D.非负数 ±2A3. 当m为何值时,函数 是反比例函数,并求出其函数解析式. 1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,曲线至左向右下降,y随x的增大而减小;2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,曲线至左向右上升, y随x的增大而增大。0位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别在同一坐标系中,正比例函数 y=(m-1)x与反比例函数 的图象大致位置不可能是 ( )利用待定系数法求函数的关系式1、按题目条件设函数的一般表达式
2、代入已知条件,得到方程组
3、解这个方程组
4、写出所求表达式
如果双曲线 经过点(-2,3),那么此双曲线也经过点( )
A.(-2,-3) B.(3,2)
C.(3,-2) D.(-3,-2)已知一次函数的图象如下图,
(1)求出这个函数的关系式;
(2)求△ABO的面积AB利用函数图象解方程组(1,1)利用函数图象解不等式 当x为何值时,(1,1)利用函数图象分析函数类型
(1)画出函数图象,分析函数的类型
(2)设相应的函数关系式
(3)求出未知系数某市出租车公司规定:出租车收费与行驶路程关系如图所示。如果小明姥姥乘出租车去小明家花了22元,那么小明姥姥乘车路程有___千米。
