第十八章 函数及其图象复习课 2(浙江省台州市)
文档属性
| 名称 | 第十八章 函数及其图象复习课 2(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-06 22:05:00 | ||
图片预览









文档简介
课件33张PPT。
首师大二附中 郭振华
2006年4月八年级数学期中复习建议
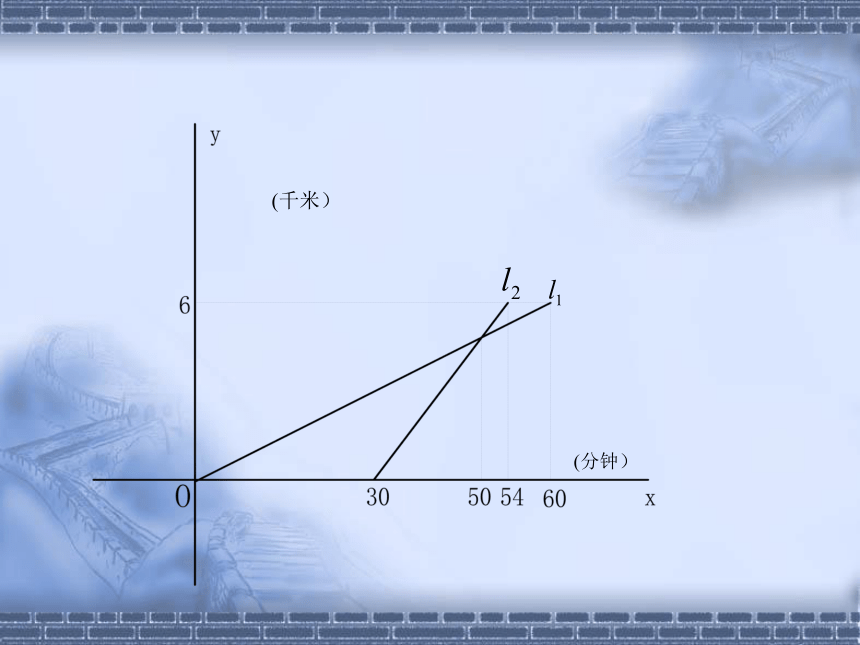
1、(河南05)某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,、分别表示步行和骑车的同学前往目的地所走的路程 (千米)与所用时间 (分钟)之间的函数图象,则以下判断错误的是( D ).
A.骑车的同学比步行的同学晚出发30分钟
B.步行的速度是6千米/时
C.骑车同学从出发到追上步行同学用了20分钟
D.骑车的同学和步行的同学同时到达目的地
(二)分类、分层由浅入深
求一次函数解析式
知一点:2、(上海05)点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是 .
知两点:3、(宁波05)已知一次函数的图象经过A(-2,-3),B(1,3)两点,
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
可转化为两点:(广西04 )
4、一次函数 的图象与 轴相交,其交点到 轴的距离为1,
求这个函数解析式.
例7.如图,点A、B的坐标分别是(-3,0),
(2,0),C点在y轴上, △ABC的面积为15.
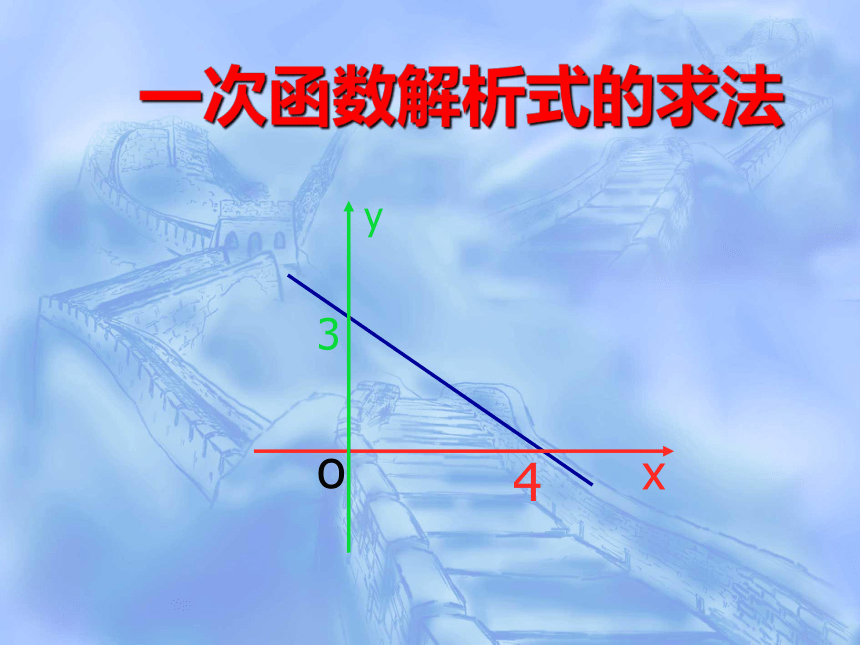
求过A、C两点的一次函数图象的解析式; 一次函数解析式的求法y一、根据定义求解析式5、已知y与x成正比例,且当x=-1时,y=-6,求y与x之间的函数关系式解:由题意可设y=kx(k≠0)
∵当x=-1时,y=-6,
∴-k=-6
∴k=6
∴y=6x
变式训练
6、已知y-2与x成正比例,当x=-2时,y=8,求y与x之间的函数关系式解:根据题意设:
y-2=kx
∴-2k=8-2
∴k=-3
y-2=-3x
∴y=-3x+2
二、已知两点坐标
求函数解析式例2:一次函数y=kx+b表示的直线 经过点A(1,2)、B(-1,-4),试求直线AB的解析式
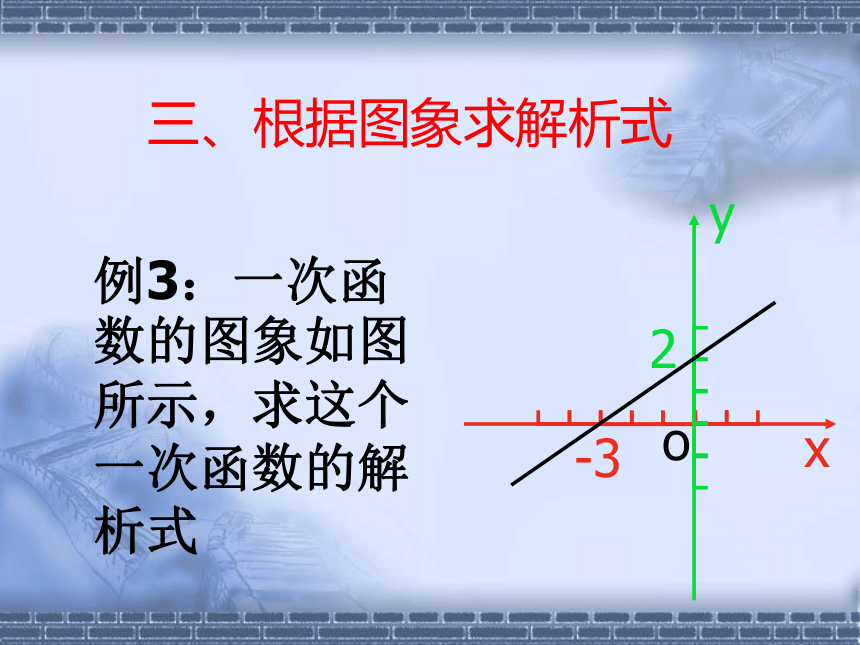
三、根据图象求解析式例3:一次函数的图象如图所示,求这个一次函数的解析式设一次函数解析式为y=kx+b
根据题意得:-3k+b=0
k×0+b=2解得:k=b=2∴y= x+2四、根据表格信息求解析式9、如图:大拇指与小拇指尽量张开时,两指尖的距离称为指距,某项研究表明,一般情况下人的身高h是指距d的一次函数,下表是测得的指距与身高的一组数据:求:h与d之间的函数关系式解:根据题意设:
h=kd+b
∴20k+b=16021k+b=169解得:k=9b=-20∴h=9d-20五、根据图象之间的平行关系求解析式四、5、将函数y=x+2的图象平移,使它经过点(1,-3),求平移后的直线所对应的函数解析式解:设所求直线的解析式为y=kx+b
根据题意得:k=1k+b=-3k=1b=-4∴y=x-4六、根据缺少的条件求解析式四、6、写出一个一次函数,使它的图象过点(-1,2)解:
设函数解析式为y=kx+b(k≠0)
由题意,得 : -k+b=2
∴b=2+k
取k=1,则b=3,有y=x+3
七、根据取值范围求解析式四、7、一次函数y=kx+b的自变量的取值范围是-3≤x ≤6,相应函数值的取值范围是-5 ≤y ≤-2,求这个函数的解析式解:要确定函数的解析式,从已知条件出发,可分两种情形讨论:
①若x=-3时,y=-5,有-3k+b=-5;x=6时,y=-2,有6k+b=-2,联立上面两式,解得k= , b=-4②若x=-3时,y=-2,有-3k+b=-2;x=6时,y=-5,有6k+b=-5,联立上面两式,解得k=- ,b=-3
故所求函数的解析式为:
y= x-4或y=- x-3一次函数y=kx+b的自变量的取值范围是-3≤x ≤6,相应函数值的取值范围是-5 ≤y ≤-2,求这个函数的解析式八、根据面积求解析式10、某一次函数的图象经过点(1,0),且和坐标轴围成的三角形面积为1,求这个一次函数的解析式解:设一次函数解析式为y=kx+b,设直线与x轴,y轴的交点分别为A,B
则A(1,0),
B(0,b)1∴S△AOB= AO×BO
= ×1× b =1
∴ b =2
∴b=±2∵直线y=kx+b过点(1,0)
∴k+b=01解k+b=0b=±2得:k=-2b=2k=2b=-2或∴y=-2x+2或y=2x-21九、根据实际问题求解析式11、已知,如图,一艘轮船在离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港),设出发x小时后,轮船离A港y千米(未到达B港),求y与x的函数关系式解:由题意可设y=kx+b(k≠0)
又当x=0时,y=10;当x= 时,y=26∴b=10
k+b=26解得:k=32
b=10∴y=32x+10应 用12、弹簧总长y(cm)与所挂物体质量x(kg)之间是一次函数关系,则该弹簧不挂物体时的长度为多少?解:设函数解析式为y=kx+b(k≠0)
由题意,得:5k+b=14.520k+b=22解得:k=0.5b=12∴一次函数解析式为
y=0.5x+12当x=0时,y=12(cm)xy52014.522 应 用
已知点A(-4,1),B(-2,5)
在x轴上求一点P,使PA+PB的和最小yxo.A.B
(三)关注知识的横向联系
例8(南昌05)在平面直角坐标系中,A、B、C
三点的坐标分别为(0,0)、(0,-5)、
(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限分类讨论思想13、 某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加2千米/小时后,沙尘暴经过开阔漠地,风速保持不变,当沙尘暴遇到绿色植被区时,其风速成平均每小时减少4千米/小时,最终停止。
结合风速与时间的图像如图,回答下列问题:
(1)在图象的( )内填入相应的数值;
(2)沙尘暴从发生到结束,
共经过多少小时?
(3)求出风速(千米/小时)与时
间(小时)之间的函数关系式.
方程思想14、.已知一次函数图象经过A(2,-1) 和点B,其中点B是另一条直线y= 5x+3与y轴的交点,求这个一次函数的解析式.
函数思想例14.今年入夏以来,全国大部分地区发生严重干旱.某市自来水公司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应交水费y(元)是用水量x(吨)的函数,当0≤x≤5时,y=0.72x,当x>5时,y=0.9x-0.9.(1)画出函数的图象;(2)观察图象,利用函数解析式,回答自来水公司采取的收费标准.THEEND
谢谢!
首师大二附中 郭振华
2006年4月八年级数学期中复习建议
1、(河南05)某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,、分别表示步行和骑车的同学前往目的地所走的路程 (千米)与所用时间 (分钟)之间的函数图象,则以下判断错误的是( D ).
A.骑车的同学比步行的同学晚出发30分钟
B.步行的速度是6千米/时
C.骑车同学从出发到追上步行同学用了20分钟
D.骑车的同学和步行的同学同时到达目的地
(二)分类、分层由浅入深
求一次函数解析式
知一点:2、(上海05)点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是 .
知两点:3、(宁波05)已知一次函数的图象经过A(-2,-3),B(1,3)两点,
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
可转化为两点:(广西04 )
4、一次函数 的图象与 轴相交,其交点到 轴的距离为1,
求这个函数解析式.
例7.如图,点A、B的坐标分别是(-3,0),
(2,0),C点在y轴上, △ABC的面积为15.
求过A、C两点的一次函数图象的解析式; 一次函数解析式的求法y一、根据定义求解析式5、已知y与x成正比例,且当x=-1时,y=-6,求y与x之间的函数关系式解:由题意可设y=kx(k≠0)
∵当x=-1时,y=-6,
∴-k=-6
∴k=6
∴y=6x
变式训练
6、已知y-2与x成正比例,当x=-2时,y=8,求y与x之间的函数关系式解:根据题意设:
y-2=kx
∴-2k=8-2
∴k=-3
y-2=-3x
∴y=-3x+2
二、已知两点坐标
求函数解析式例2:一次函数y=kx+b表示的直线 经过点A(1,2)、B(-1,-4),试求直线AB的解析式
三、根据图象求解析式例3:一次函数的图象如图所示,求这个一次函数的解析式设一次函数解析式为y=kx+b
根据题意得:-3k+b=0
k×0+b=2解得:k=b=2∴y= x+2四、根据表格信息求解析式9、如图:大拇指与小拇指尽量张开时,两指尖的距离称为指距,某项研究表明,一般情况下人的身高h是指距d的一次函数,下表是测得的指距与身高的一组数据:求:h与d之间的函数关系式解:根据题意设:
h=kd+b
∴20k+b=16021k+b=169解得:k=9b=-20∴h=9d-20五、根据图象之间的平行关系求解析式四、5、将函数y=x+2的图象平移,使它经过点(1,-3),求平移后的直线所对应的函数解析式解:设所求直线的解析式为y=kx+b
根据题意得:k=1k+b=-3k=1b=-4∴y=x-4六、根据缺少的条件求解析式四、6、写出一个一次函数,使它的图象过点(-1,2)解:
设函数解析式为y=kx+b(k≠0)
由题意,得 : -k+b=2
∴b=2+k
取k=1,则b=3,有y=x+3
七、根据取值范围求解析式四、7、一次函数y=kx+b的自变量的取值范围是-3≤x ≤6,相应函数值的取值范围是-5 ≤y ≤-2,求这个函数的解析式解:要确定函数的解析式,从已知条件出发,可分两种情形讨论:
①若x=-3时,y=-5,有-3k+b=-5;x=6时,y=-2,有6k+b=-2,联立上面两式,解得k= , b=-4②若x=-3时,y=-2,有-3k+b=-2;x=6时,y=-5,有6k+b=-5,联立上面两式,解得k=- ,b=-3
故所求函数的解析式为:
y= x-4或y=- x-3一次函数y=kx+b的自变量的取值范围是-3≤x ≤6,相应函数值的取值范围是-5 ≤y ≤-2,求这个函数的解析式八、根据面积求解析式10、某一次函数的图象经过点(1,0),且和坐标轴围成的三角形面积为1,求这个一次函数的解析式解:设一次函数解析式为y=kx+b,设直线与x轴,y轴的交点分别为A,B
则A(1,0),
B(0,b)1∴S△AOB= AO×BO
= ×1× b =1
∴ b =2
∴b=±2∵直线y=kx+b过点(1,0)
∴k+b=01解k+b=0b=±2得:k=-2b=2k=2b=-2或∴y=-2x+2或y=2x-21九、根据实际问题求解析式11、已知,如图,一艘轮船在离A港10千米的P地出发向B港匀速行驶,30分钟后离A港26千米(未到达B港),设出发x小时后,轮船离A港y千米(未到达B港),求y与x的函数关系式解:由题意可设y=kx+b(k≠0)
又当x=0时,y=10;当x= 时,y=26∴b=10
k+b=26解得:k=32
b=10∴y=32x+10应 用12、弹簧总长y(cm)与所挂物体质量x(kg)之间是一次函数关系,则该弹簧不挂物体时的长度为多少?解:设函数解析式为y=kx+b(k≠0)
由题意,得:5k+b=14.520k+b=22解得:k=0.5b=12∴一次函数解析式为
y=0.5x+12当x=0时,y=12(cm)xy52014.522 应 用
已知点A(-4,1),B(-2,5)
在x轴上求一点P,使PA+PB的和最小yxo.A.B
(三)关注知识的横向联系
例8(南昌05)在平面直角坐标系中,A、B、C
三点的坐标分别为(0,0)、(0,-5)、
(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限分类讨论思想13、 某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加2千米/小时后,沙尘暴经过开阔漠地,风速保持不变,当沙尘暴遇到绿色植被区时,其风速成平均每小时减少4千米/小时,最终停止。
结合风速与时间的图像如图,回答下列问题:
(1)在图象的( )内填入相应的数值;
(2)沙尘暴从发生到结束,
共经过多少小时?
(3)求出风速(千米/小时)与时
间(小时)之间的函数关系式.
方程思想14、.已知一次函数图象经过A(2,-1) 和点B,其中点B是另一条直线y= 5x+3与y轴的交点,求这个一次函数的解析式.
函数思想例14.今年入夏以来,全国大部分地区发生严重干旱.某市自来水公司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应交水费y(元)是用水量x(吨)的函数,当0≤x≤5时,y=0.72x,当x>5时,y=0.9x-0.9.(1)画出函数的图象;(2)观察图象,利用函数解析式,回答自来水公司采取的收费标准.THEEND
谢谢!
