解直角三角形
图片预览




文档简介
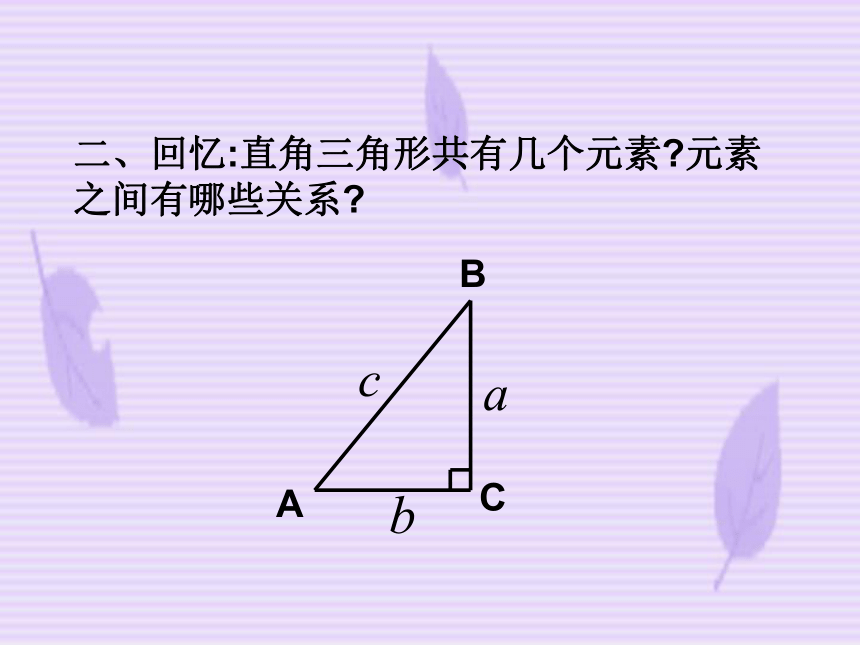
课件19张PPT。解直角三角形的应用二、回忆:直角三角形共有几个元素?元素之间有哪些关系?1、三边之间的关系:2、锐角之间的关系:3、边角之间的关系:利用以上的关系式,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素。在直角三角形中,由已知元素求出所有未知元素的过程,叫做解直角三角形。 1、在直角△ABC中,∠C=90° ∠A=30°
AC=5 ,则BC= , AB= ,
∠B= 。 2、在直角△ABC中, ∠C=90° AC=2 ,
BC=2,则∠A= ,∠B= ,AB= 。3、在△ABC中,AD为BC边上的高,
BD=AD= ,CD=1,则∠BAC= 。 4、在直角△ABC中, ∠C=90° ∠A=30°,
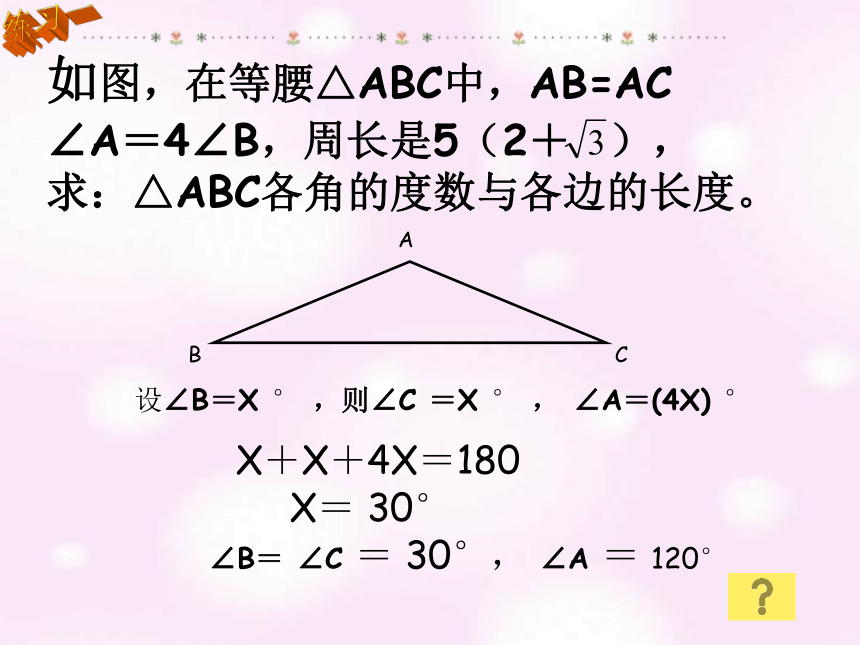
a+b=2,则a= 。复习引入51060°60°30°475°或15°如图,在等腰△ABC中,AB=AC
∠A=4∠B,周长是5(2+ ),
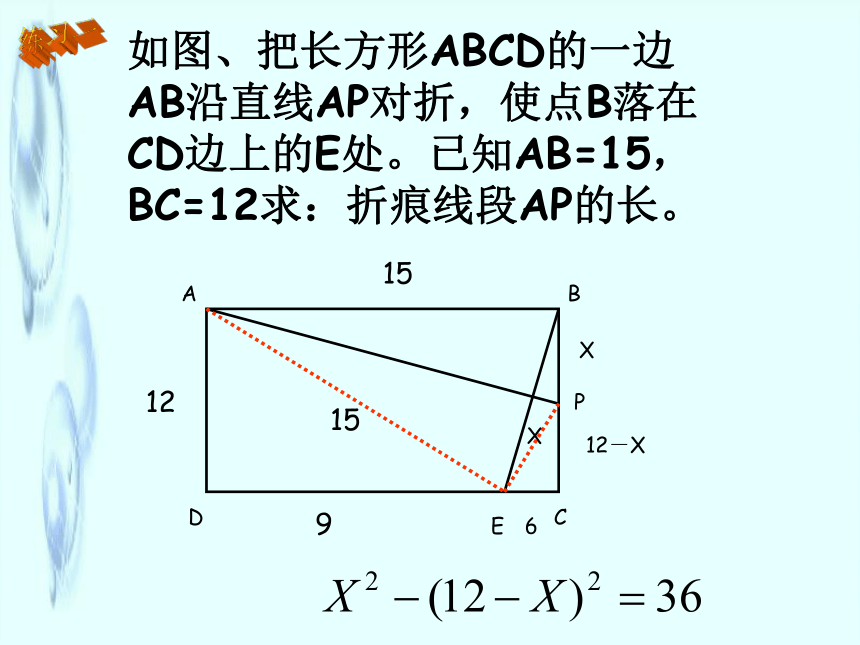
求:△ABC各角的度数与各边的长度。练习一设∠B=X ° ,则∠C =X ° , ∠A=(4X) °X+X+4X=180X= 30°∠B= ∠C = 30°, ∠A = 120°如图、把长方形ABCD的一边AB沿直线AP对折,使点B落在CD边上的E处。已知AB=15,BC=12求:折痕线段AP的长。练习二15121596XX12-X如图,河对岸岸边有一点A,在河边沿河取B、C使∠ABC=60°∠ACB=45°量得BC=30米。求:河的宽度。练习三D练习四如图,为了求河对岸塔高AB,先选定
两点C与D,且使∠CBD=90°,
然后测得CD的长为10米,塔顶A的仰角
α=30°,β=45°,试求塔高AB。开动脑筋请为测量上题中的塔高
AB设计一个可行的方案小结 1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。 2.设未知数得到相关的方程,是解题的一个关键步骤,应用了方程的思想,将几何图形的计算转化为解代数方程。
谢谢您光临指导再见ABCX2XX30°ABCDX2X2XXX2X+2X+2 X=5(2+ )30°30°2X(2+ )=5(2+ )X=2.560°45°XXXα=30°XXβ=45°XXXX102X=ABC方案ABCDXBC-BD=DCαβ方案
AC=5 ,则BC= , AB= ,
∠B= 。 2、在直角△ABC中, ∠C=90° AC=2 ,
BC=2,则∠A= ,∠B= ,AB= 。3、在△ABC中,AD为BC边上的高,
BD=AD= ,CD=1,则∠BAC= 。 4、在直角△ABC中, ∠C=90° ∠A=30°,
a+b=2,则a= 。复习引入51060°60°30°475°或15°如图,在等腰△ABC中,AB=AC
∠A=4∠B,周长是5(2+ ),
求:△ABC各角的度数与各边的长度。练习一设∠B=X ° ,则∠C =X ° , ∠A=(4X) °X+X+4X=180X= 30°∠B= ∠C = 30°, ∠A = 120°如图、把长方形ABCD的一边AB沿直线AP对折,使点B落在CD边上的E处。已知AB=15,BC=12求:折痕线段AP的长。练习二15121596XX12-X如图,河对岸岸边有一点A,在河边沿河取B、C使∠ABC=60°∠ACB=45°量得BC=30米。求:河的宽度。练习三D练习四如图,为了求河对岸塔高AB,先选定
两点C与D,且使∠CBD=90°,
然后测得CD的长为10米,塔顶A的仰角
α=30°,β=45°,试求塔高AB。开动脑筋请为测量上题中的塔高
AB设计一个可行的方案小结 1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。 2.设未知数得到相关的方程,是解题的一个关键步骤,应用了方程的思想,将几何图形的计算转化为解代数方程。
谢谢您光临指导再见ABCX2XX30°ABCDX2X2XXX2X+2X+2 X=5(2+ )30°30°2X(2+ )=5(2+ )X=2.560°45°XXXα=30°XXβ=45°XXXX102X=ABC方案ABCDXBC-BD=DCαβ方案
