云南通海二中2017届高一数学必修一第二章指数函数课件
文档属性
| 名称 | 云南通海二中2017届高一数学必修一第二章指数函数课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-24 08:50:56 | ||
图片预览






文档简介
课件17张PPT。第二章 基本初等函数(Ⅰ)2.1 指数函数
2.2 对数函数
2.3 幂函数前言:
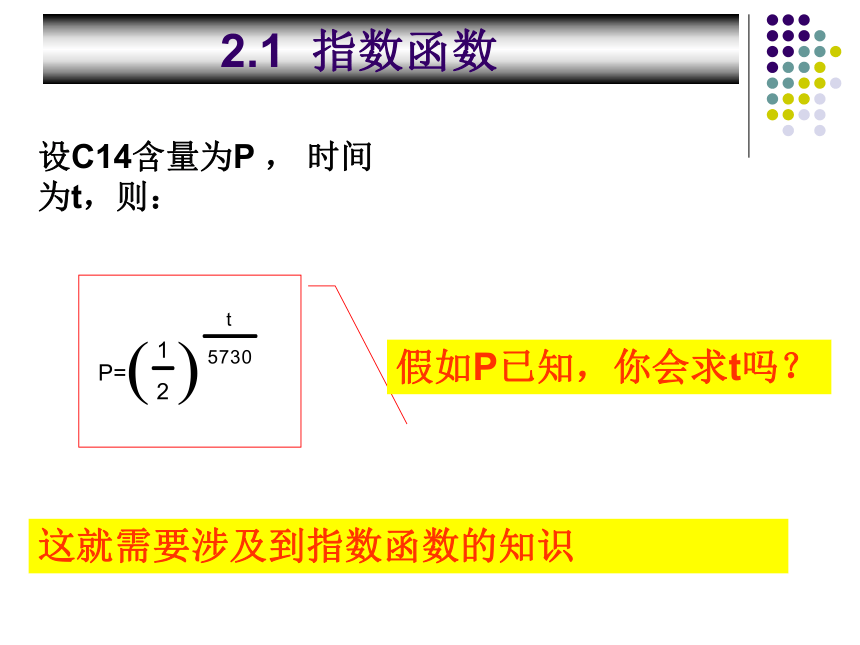
例1:著名的楼兰新娘埋葬于3800年前人们是如何测算的?C14与生物体C14测年法:宇宙射线在大气层中能够产生放射性C14,并与氧结合成 后进入所有活组织,先为植物吸收,再为动物吸收,只要植物和动物生存着,它们就会不断地吸收C14在机体内保持一定的水平。而当有机体死亡后,即会停止吸收C14,其组织内的C14便以约5730年的半衰期开始衰变并消失。对于任何含碳物质只要测定剩下的放射性C14的含量,便可推断其年代。(半衰期:经过一定时间,变为原来的一半)楼兰新娘复原图设C14含量为P , 时间为t,则:
这就需要涉及到指数函数的知识假如P已知,你会求t吗? 2.1 指数函数前言:
例2:细胞有丝分裂是一个分裂为两个,两个个分裂为四个,四个分裂为八个….问题:从一个细胞分裂成128个需要分裂几次?第一次后第二次后第三次后 128个细胞有没有规律?设第x次分裂后细胞个数为y,则:第x次后学习本章内容后我们就可以求解x了2.1.1 指数与指数幂的运算知识回顾:1.什么是平方根?立方根?一个数的平方根有几个?立方根呢?答:中x即为a的平方根,或称a的二次方根中x即为a的立方根,或称a的三次方根 可以看出数的平方根、立方根是n次方根概念里面的两个特例知识探索:一般地,如果 ,那么x叫做a的n次方根,其中,n>1且n ∈ 。你能根据“n次方根”的意义求出下列数的n次方根吗?①4的平方根?
② 8的立方根?
③-8的立方根?
④ 16的4次方根?
⑤ 32的5次方根?
⑥-32的5次方根?
0的7次方根?
⑧ 的立方根
答:①②2;③ -2 ;④ ⑤2;⑥-2;0;⑧ ;观察思考:在上例①至⑧中,n分别是奇数还是偶数?不同的n,对应的根又有什么特点? n为奇数 n为偶数a有一个n次方根a有两个n次方根,且两根互为相反数①中欲求偶次方根,此时有两个根+2和-2
②中欲求奇次方根,此时有一个根+2;
③中欲求奇次方根,此时有一个 根-2;
④中欲求偶次方根,此时有两个根+2和-2
⑤中欲求奇次方根,此时有一个 根+2;
⑥中欲求奇次方根,此时有一个 根-2;
⑦中欲求奇次方根,此时有一个根0;
⑧中欲求奇次方根,此时有一个 根注意:0的任何次方根都是0请问:任何一个数a的偶次方根是否总是存在呢?结合刚才的讨论,我们得到n次方根的性质:
①当n为偶数时,a的n次方根有两个,并互为相反数,正的n次方根用 表示,负的n次方根用 表示 ,这两根可以合并写成 ;
②当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时a的n次方根用 表示;
③负数没有偶次方根,0的任何次方根都是0。上面的文字语言可以用下面的式子表示为:现在我们给式子 起一个名字——根式。根式的概念:式子 叫做根式,其中a叫做被开方数,n叫做根指数;例如: 中,3叫做根指数,-64叫做被开方数。思考:表示 的n次方根,等式 一定成立吗?如果不一定成立,那么 等于什么?如:通过探究我们得到:n为奇数n为偶数刚才讨论的是 ,那么 呢?实际上, 中由于a在根号里面,所以a不可能为负数,因此 恒成立。 请看第50页例1练习1.求出下列各式的值。①②③-23a-32.下列各式中正确的是( )A.B.C.D.D3.求值:解:4.下列说法中正确的是( )A.正数的n次方根是一个正数;
B.负数的n次方根是一个负数;
C.0的任何次方根都是负数;
D.a的n次方根用 表示 。C5.化简下列各式:(1) (2) (3) (4) (5) (6)再见
2.2 对数函数
2.3 幂函数前言:
例1:著名的楼兰新娘埋葬于3800年前人们是如何测算的?C14与生物体C14测年法:宇宙射线在大气层中能够产生放射性C14,并与氧结合成 后进入所有活组织,先为植物吸收,再为动物吸收,只要植物和动物生存着,它们就会不断地吸收C14在机体内保持一定的水平。而当有机体死亡后,即会停止吸收C14,其组织内的C14便以约5730年的半衰期开始衰变并消失。对于任何含碳物质只要测定剩下的放射性C14的含量,便可推断其年代。(半衰期:经过一定时间,变为原来的一半)楼兰新娘复原图设C14含量为P , 时间为t,则:
这就需要涉及到指数函数的知识假如P已知,你会求t吗? 2.1 指数函数前言:
例2:细胞有丝分裂是一个分裂为两个,两个个分裂为四个,四个分裂为八个….问题:从一个细胞分裂成128个需要分裂几次?第一次后第二次后第三次后 128个细胞有没有规律?设第x次分裂后细胞个数为y,则:第x次后学习本章内容后我们就可以求解x了2.1.1 指数与指数幂的运算知识回顾:1.什么是平方根?立方根?一个数的平方根有几个?立方根呢?答:中x即为a的平方根,或称a的二次方根中x即为a的立方根,或称a的三次方根 可以看出数的平方根、立方根是n次方根概念里面的两个特例知识探索:一般地,如果 ,那么x叫做a的n次方根,其中,n>1且n ∈ 。你能根据“n次方根”的意义求出下列数的n次方根吗?①4的平方根?
② 8的立方根?
③-8的立方根?
④ 16的4次方根?
⑤ 32的5次方根?
⑥-32的5次方根?
0的7次方根?
⑧ 的立方根
答:①②2;③ -2 ;④ ⑤2;⑥-2;0;⑧ ;观察思考:在上例①至⑧中,n分别是奇数还是偶数?不同的n,对应的根又有什么特点? n为奇数 n为偶数a有一个n次方根a有两个n次方根,且两根互为相反数①中欲求偶次方根,此时有两个根+2和-2
②中欲求奇次方根,此时有一个根+2;
③中欲求奇次方根,此时有一个 根-2;
④中欲求偶次方根,此时有两个根+2和-2
⑤中欲求奇次方根,此时有一个 根+2;
⑥中欲求奇次方根,此时有一个 根-2;
⑦中欲求奇次方根,此时有一个根0;
⑧中欲求奇次方根,此时有一个 根注意:0的任何次方根都是0请问:任何一个数a的偶次方根是否总是存在呢?结合刚才的讨论,我们得到n次方根的性质:
①当n为偶数时,a的n次方根有两个,并互为相反数,正的n次方根用 表示,负的n次方根用 表示 ,这两根可以合并写成 ;
②当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时a的n次方根用 表示;
③负数没有偶次方根,0的任何次方根都是0。上面的文字语言可以用下面的式子表示为:现在我们给式子 起一个名字——根式。根式的概念:式子 叫做根式,其中a叫做被开方数,n叫做根指数;例如: 中,3叫做根指数,-64叫做被开方数。思考:表示 的n次方根,等式 一定成立吗?如果不一定成立,那么 等于什么?如:通过探究我们得到:n为奇数n为偶数刚才讨论的是 ,那么 呢?实际上, 中由于a在根号里面,所以a不可能为负数,因此 恒成立。 请看第50页例1练习1.求出下列各式的值。①②③-23a-32.下列各式中正确的是( )A.B.C.D.D3.求值:解:4.下列说法中正确的是( )A.正数的n次方根是一个正数;
B.负数的n次方根是一个负数;
C.0的任何次方根都是负数;
D.a的n次方根用 表示 。C5.化简下列各式:(1) (2) (3) (4) (5) (6)再见
