人教版六年级上册数学第三单元《分数除法》整单元课件(153张PPT)
文档属性
| 名称 | 人教版六年级上册数学第三单元《分数除法》整单元课件(153张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 10:36:59 | ||
图片预览










文档简介
(共153张PPT)
倒数的认识
3
R·六年级上册 第三单元 分数除法
文字里有趣的变化!
一、新课导入
呆—杏 音—昱
吞—吴 甲—由
数学里也有这样有趣的变化!
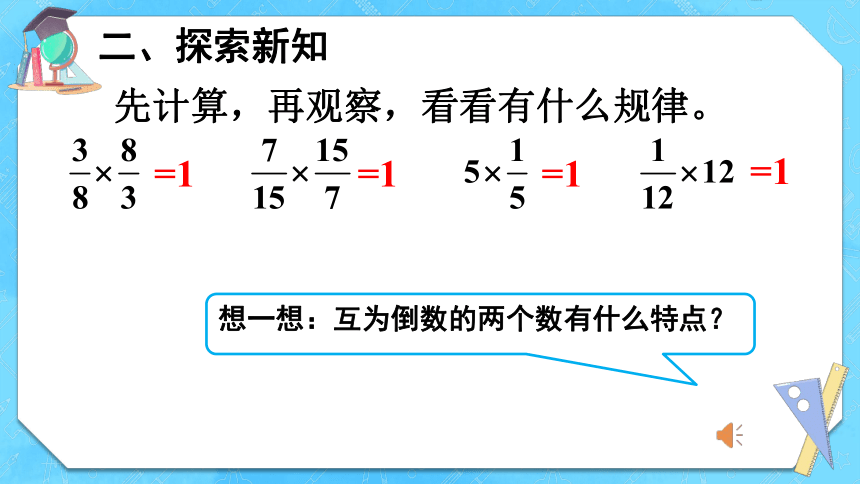
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
相乘的两个数的分子、分母正好颠倒了位置。
这几个算式的乘积都是1
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
乘积是1的两个数互为倒数。
和 互为倒数,就是指 的倒数是 , 的倒数是 。
(1)
+ =1,所以
和 互为倒数 。( )
(2)
× × = 1 ,所以
,
,
互为倒数 。( )
(3)
× =1,所以
是倒数 。( )
×
×
×
(4)
与 的乘积为1,所以
和 互为倒数 。( )
下面的说法对不对,为什么?
√
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
想一想:互为倒数的两个数有什么特点?
你是怎样找一个数的倒数的?
下面哪两个数互为倒数?
6
1
0
分子、分母交换位置
分子、分母交换位置
6 的倒数是
的倒数是
分子、分母交换位置
的倒数是
1的倒数是多少?0有倒数吗?和同学交流一下你的想法。
1×1=1 1的倒数是1。0乘任何数都得0,0没有倒数。
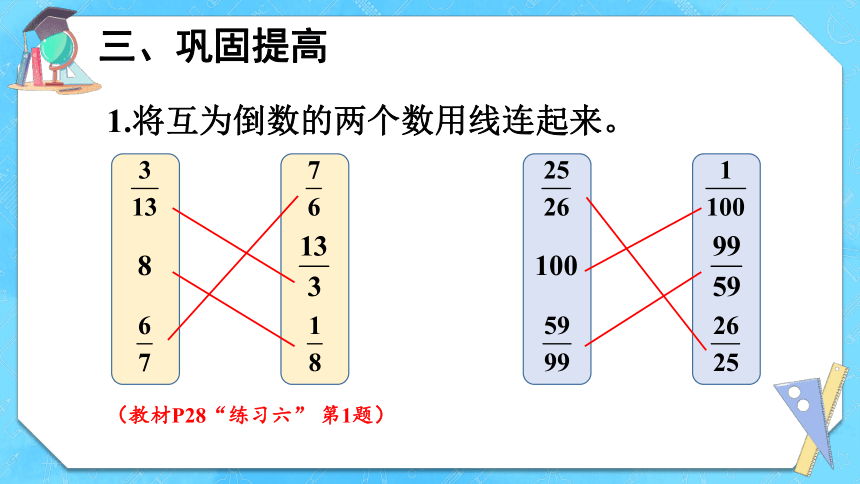
1.将互为倒数的两个数用线连起来。
三、巩固提高
(教材P28“练习六” 第1题)
2.写出下面各数的倒数。
三、巩固提高
的倒数是 ;
的倒数是 ;
的倒数是 ;
的倒数是 ;
1.25
的倒数是 ;
1.25的倒数是 。
5
4
(教材P27 做一做)
3.填空。
(1)
(2)( )的倒数是它本身,( )没有倒数。
(3) 的倒数是( ),9的倒数是( ),2.5的倒数是( )。
4.先计算出每组算式的结果,再在 里填上“>”“<”或“=”。
=
=
=
(教材P28“练习六” 第4题)
四、课堂小结
通过今天的学习你有什么收获?
乘积是1的两个数互为倒数。
五、课后作业
完成对应课时的练习。
分数除以整数
3
R·六年级上册
一、复习导入
1.说出下面各数的倒数。
4
5
1
7
1
4
5
3
2
1
一、复习导入
2.计算下列各题。
1.5×3
2.3×4
=4.5
=9.2
4.5÷3
9.2÷4
=1.5
=2.3
比较两组算式,你有什么发现?
除法是乘法的逆运算。
二、探索新知
1.探究分数除法的意义。
(1)每盒水果糖重 kg,3盒有多重
(2)3盒水果糖重 kg,每盒有多重
分数除法与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
二、探索新知
怎样列式计算呢?
你能在图中表示出结果吗?
2.探究分数除以整数的计算方法。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
把 平均分成2份,就是把4个 平均分成2份,每份是2个 ,就是 。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
把 平均分成2份,每份就是 的 ,也就是 。
思考:把这张纸的 平均分成3份,每份是这张纸的多少?
___×___=___
说一说,这里把÷3写成× 后再计算,你是怎样想的?
把 平均分成3份,就是求 的 。
根据上面的折纸实验和算式,你能发现什么规律?
分数除以整数(0除外)等于分数乘这个整数的倒数。
1.计算下面各题。
9
10
3
1
10
3
3
8
2
1
3
16
三、巩固提高
×
(教材P29“做一做” )
2.先算出乘法算式的得数,再根据左右两题之间的关系,写出除法算式的得数。
3.小芳将长 m的丝带剪成同样长的8段,每段丝带有多长
答:每段丝带有 米。
(教材P33“练习七” 第2题)
4.填一填。
(教材P33“练习七” 第3题)
分数除以整数(0除外)等于分数乘这个整数的倒数。
四、课堂小结
分数除法与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
五、课后作业
完成对应课时的练习。
一个数除以分数
3
R·六年级上册
1.一辆汽车2小时行驶90千米,平均每小时行驶多少千米?
一、复习导入
2.计算下面各题,直接写出答案。
速度=路程÷时间
90÷2=45(千米/时)
分数除以整数(0除外)等于分数乘这个整数的倒数。
二、探索新知
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
怎么计算呢? 画个图试试吧。
先求 小时走的千米数,也就是求2km的 ,即
3个 小时走的千米数也就是1小时走的千米数,再乘3,即
1
1
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
所以小明走得快些。
1
1
1
1
2
1
3km>2km
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
通过上面的计算,你发现了什么?你会用自己的方式表示你发现的规律吗?
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
除以一个不等于0的数,等于乘这个数的倒数。
甲数÷乙数(0除外)=甲数×乙数的倒数
1.计算下面各题。
9
8
27
×
7
16
5
4
×
三、巩固提高
(教材P31“做一做”第1题)
2.计算下面各题。
(教材P31“做一做” 第2题)
3.不用计算,你知道下面哪几道题的商大于被除数、哪几道题的商小于被除数吗
商小于被除数的:
商大于被除数的:
(教材P31“做一做” 第3题)
4.计算下面各题。
(教材P33“练习七” 第4题)
5.把 L橙汁分装在容量是 L的小瓶里,可以装满几瓶
答:可以装满3瓶。
(教材P33“练习七” 第5题)
甲数÷乙数(0除外)=甲数×乙数的倒数
四、课堂小结
一个数除以分数
整数除以分数
分数除以分数
=3
除以一个不等于0的数,等于乘这个数的倒数。
五、课后作业
完成对应课时的练习。
分数混合运算
3
R·六年级上册
说出运算顺序,不用计算。
(18+7)×4 88+30÷5 350-25×2 60÷(77-65)
①
②
一、复习导入
①同级运算,按从左往右的运算顺序进行计算
②两级运算,先算乘法或除法再算加法或减法
③有括号的要先算括号里面的
二、探索新知
一盒药共12片,每次吃半片,每天吃3次。这盒药可以吃几天?
片
一盒药共12片,每次吃半片,每天吃3次。这盒药可以吃几天?
我先算每天吃多少片。
我先算这盒药可以吃几次。
也可以用综合算式表示以上过程,自己试着计算一下。
分数四则运算的顺序和整数一样。
说一说,你是按怎样的顺序计算的?
1.计算下面各题。
(教材P32“做一做”第1题 )
2.一块梯形的玻璃,上底、下底和高分别是
这块玻璃的面积是多少?
( + )× ÷2
5
3
5
4
4
3
答:这块玻璃的面积是 m2 。
= × ×
5
7
4
3
2
1
= (m2)
40
21
(教材P32“做一做”第2题 )
1. 计算下面各题。
三、巩固提高
(教材P34“练习七” 第8题)
2. 李爷爷每天慢跑6圈,他跑半圈大约用2分钟。照这个速度,李爷爷每天慢跑大约要用多少时间?
答:李爷爷每天慢跑大约要用24分钟。
(教材P34“练习七” 第9题)
3.一幢楼共有15 层(如右图)。小萍家住7 楼,她家的地板离地面有多高?
答:小萍家的地板离地20m。
(教材P34“练习七” 第10题)
10
1
2
3
四、课堂小结
分数四则运算的计算顺序和整数四则运算顺序一样。
五、课后作业
完成对应课时的练习。
练习课(第1~3课时)
3
R·六年级上册
一、复习巩固
关于分数除法,你知道了什么
如果两个数的乘积是1,那么这两个数互为倒数,且其中一个数是另一个数的倒数。
1的倒数是1,0没有倒数。
除以一个不为0的数,等于乘这个数的倒数。
分数四则混合运算与整数四则混合运算的运算顺序相同。
二、基础练习
1.填一填。
求一个因数,要用积除以另一个因数。分数除法的意义与整数除法相同。
2.计算下面各题。
(教材P34“练习七” 第12题)
2.计算下面各题。
(教材P34“练习七” 第12题)
3.某饮料厂使用一种自动检测仪检测饮料瓶是否有缺陷,检测一个瓶子所用的时间为 秒。1分钟可以检测多少个瓶子
1分=60秒
答:1分钟可以检测1500个瓶子。
(教材P33“练习七” 第6题)
4.我们平时看到的电影画面实际上是由许多连续拍摄的照片以每 秒一张的速度连续播放的。请你算一算:半秒可以播放多少张照片? 1 分钟呢?
1分=60秒
答:半秒可以播放12张照片,1分钟可以播放1440张照片。
(教材P33“练习七” 第7题)
三、综合练习
1.有240 kg水果糖需要装袋,每袋装 kg,已经装完了总量的 。装完了多少袋?
答:装完了720袋。
(教材P34“练习七” 第11题)
2.解下列方程。
(教材P34“练习七” 第13题)
2.解下列方程。
(教材P34“练习七” 第13题)
3. 一盏节能灯1小时耗电 千瓦时,某个传达室除了这盏节能灯外,没有别的电器。这个传达室上个月的用电量是 千瓦时,这盏灯上个月共使用了多少小时
答:这盏灯上个月共使用了100小时。
(教材P34“练习七” 第14题)
4. 某种手机的自动化生产线在手机机板上插入每个零件的时间仅为 秒。3分钟可以插入多少个零件
3分=180秒
答:3分钟可以插入2000个零件。
(教材P34“练习七” 第15题)
四、拓展练习
按下面的步骤计算,再把最后的得数与开始的数比较,你能发现什么 你知道为什么吗
=
2
3
×
3
4
×
2
1
×
1
1
1
1
=
1
五、课后作业
完成对应课时的练习。
解决问题(1)
3
R·六年级上册
一、复习导入
找出单位“1”,并列出数量关系式。
(1)每把椅子的价钱相当于每张桌子的价钱的 。
5
4
“1”
每张桌子的价钱 × =每把椅子的价钱
5
4
(2)男生人数是女生人数的 。
7
6
“1”
女生人数 × =男生人数
7
6
单位“1”的量×对应的分率=对应的量
二、探索新知
阅读与理解
小明体内的水分重 _______。
小明体内的水分占体重的 ____。
要求的是小明的______。
28kg
体重
(教材P35例4)
分析与解答
水分28kg
体重?kg
水分占体重的
根据“儿童体内的水分占体重的 ”可以列出下面的关系式。
小明的体重× =小明体内水分的质量
分析与解答
水分28kg
体重?kg
水分占体重的
小明的体重× =小明体内水分的质量
解:设小明的体重是x千克。
回顾与反思
看结果是不是小明体内水分的质量。
答:小明的体重是35kg。
28
回顾与反思
解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:
1.找出单位“1”,设未知量为 x;
2.找出题中的数量关系式;
3.列出方程并解答;
4.检验并写出答案。
小明的体重× =小明体内水分的质量
答:小明的体重是35kg。
分析与解答
水分28kg
体重?kg
水分占体重的
小明的体重× =小明体内水分的质量
28 ÷ = 28× = 35(kg)
5
4
4
5
答:小明的体重是 35 kg。
三、巩固提高
1.我国幅员辽阔,东西相距约5200km,东西距离是南北的 。南北相距约多少千米?
(教材P37“练习八” 第1题)
南北距离× =东西距离
解:设南北相距约x千米。
x=5200
x=5200÷
55
52
x=5200×
52
55
x=5500
答:南北相距约5500千米。
2.一杯250mL的鲜牛奶大约含有 g的钙质,占一个成年人一天所需钙质的 。一个成年人一天大约需要多少钙质
答:一个成年人一天大约需要 g钙质。
(教材P37“练习八” 第2题)
成人一天所需钙质的质量× = g的钙质
解:设一个成年人一天大约需要xg的钙质。
x=
x= ÷
8
3
x=
3.神舟十号载人飞船在轨飞行约15 天,相当于神舟十三号载人飞船在轨飞行时间的 。神舟十三号载人飞船在轨飞行约多少天?
答:神舟十三号载人飞船在轨飞行约183天。
神舟十三号在轨飞行的天数× =神舟十号在轨飞行的天数
(教材P37“练习八” 第3题)
四、课堂小结
明确数量关系—确定单位“1” —列式解答。
28÷ =28× =35(kg)
5
4
4
5
五、课后作业
完成对应课时的练习。
解决问题(2)
3
R·六年级上册
一只大熊猫的寿命约为20年,相当于大猩猩的 。大猩猩的寿命约是多少年
答:大猩猩的寿命约是50年。
一、新课导入
解:设大猩猩的寿命约是x年。
x=20
x=20÷
5
2
x=50
5
2
大猩猩的寿命× =大熊猫的寿命
5
2
二、探索新知
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
阅读与理解
小明的体重是_______。
小明的体重比爸爸轻______。
要求的是___________的体重。
35kg
小明爸爸
(教材P36例5)
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
该怎么画线段图?
爸爸:
小明:
35kg
小明的体重比爸爸轻
是爸爸的体重的几分之几?
?kg
爸爸的体重×(1- )=小明的体重
爸爸的体重-小明比爸爸轻的部分=小明的体重
解:设小明爸爸的体重是xkg。
35÷(1- )=75(kg)
爸爸的体重×(1- )=小明的体重
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
解:设小明爸爸的体重是xkg。
爸爸的体重-小明比爸爸轻的部分=小明的体重
答:小明爸爸的体重是75千克。
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
(75-35 )÷75 =
答:小明爸爸的体重是75kg。
看看小明是否比爸爸轻 。
回顾与反思
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
解决“已知比一个数多(少)几分之几是多少,求这个数”的问题的一般方法:
1.找出单位“1”。
2.写出题中的数量关系式。
3.列式或者列方程解答。
4.检验并写出答案。
35÷(1- )=75(千克)
答:小明爸爸的体重是75千克。
1.写出题中的等量关系式。
(1)红花有20朵,比黄花多 ,黄花有多少朵?
(2)一批货物,运走了 ,还剩下 t,这批货物重多少吨?
黄花的朵数+黄花朵数× =红花的朵数
原货物质量-原货物质量× = t
三、巩固提高
解:设爸爸每月的工资为x元。
答:爸爸每月的工资为3125元。
2.妈妈每月的工资是2500元,比爸爸的工资少 。
爸爸每月的工资是多少元?
3.小东读一本课外读物,已经读了35页,还剩下 没有读。这本课外读物一共有多少页
解:设这本课外读物一共有x页。
(教材P38“练习八” 第7题)
x=35
x=35÷
x=35×
x=49
答:这本课外读物一共有49页。
4.运送一批大米,运了4车才运走 。平均每车运走这批大米的几分之几 剩下的大米还要几车才能运完
答:平均每车运走这批大米的 ,剩下的大米还要10车才能运完。
(教材P38“练习八” 第9题)
5.有一组互相咬合的齿轮。
(1)大齿轮有140个齿,小齿轮的齿数是大齿轮的 。小齿轮有多少个齿
答:小齿轮有28个齿。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(2) 小齿轮有28个齿,是大齿轮的 。大齿轮有多少个齿
答:大齿轮有140个齿。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(3)小齿轮每分钟转400周,大齿轮每分钟转的周数比小齿轮少 。大齿轮每分钟转多少周
答:大齿轮每分钟转80周。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(4)大齿轮每分钟转80周,比小齿轮每分钟转的周数少 。小齿轮每分钟转多少周
答:小齿轮每分钟转400周。
小齿轮每分钟转的周数×(1- )=大齿轮每分钟转的周数
(教材P40“练习八” 第10题)
四、课堂小结
说一说,我们是怎样解决问题的?
1.找出单位“1”。
2.写出题中的数量关系式。
3.列式或者列方程解答。
4.检验并写出答案。
五、课后作业
完成对应课时的练习。
解决问题(3)
3
R·六年级上册
一、新课导入
计算下面各题。
六年级举行篮球比赛。六(1)班全场得了42 分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
二、探索新知
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
阅读与理解
知道了全场得分_______
下半场得分是上半场得分的____。
42分
求上半场和下半场的得分各是多少。
分析与解答
解:设上半场得了x分,则下半场得了 x分。
下半场得分: (分)
上半场得分+下半场得分=42分
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
也可以想成上半场的得分是下半场的2倍。
还可以怎么做呢?
分析与解答
解:设下半场得了x分,则上半场得了2x分。
上半场得分: 14×2=28(分)
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
28+14=42,全场得分确实是42分。
14÷28= ,下半场得分确实是上半场的一半。
答:上半场得28分,下半场得14分。
回顾与反思
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
回顾与反思
确定数量关系--设单位“1”的量为x,另一个量用含有x的式子表示--列方程解答
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
1.小丽和小华共收集了36张邮票,小丽收集的张数
是小华的3倍。小丽和小华各收集了多少张邮票?
解:设小华收集了x张邮票,则小丽收集了3x张邮票。
x+3x=36
4x=36
x=9
小丽收集的邮票:3×9=27(张)
答:小丽收集了27张邮票,小华收集了9张。
三、巩固提高
2.某电视机厂去年全年生产电视机108万台,其中上半年产量是下半年的 。这个电视机厂去年上半年和下半年的产量分别是多少万台
解:设下半年产量是x万台,则上半年产量是 万台。
答:上半年产量为48万台,下半年产量为60万台。
(教材P42“练习九” 第1题)
3.武汉长江大桥全长约1670m,其中引桥的长度是正桥的 。这座大桥的正桥和引桥的长度
分别是多少米
解:设大桥正桥的长度为x米,则引桥的长度为 米。
答:大桥正桥的长度为1156米,则引桥的长度为514米。
(教材P42“练习九” 第4题)
4.中国二十四节气中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的黑夜时长是白昼时长的 。白昼和黑夜分别是多少小时
解:设这一天北京白昼为x小时,则黑夜为 小时。
答:这一天北京白昼为15小时,黑夜为9小时。
(教材P42“练习九” 第5题)
四、课堂小结
说一说,怎样列方程解决求2个未知数的问题?
确定数量关系--设单位“1”的量为x,另一个量用含有x的式子表示--列方程解答
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
五、课后作业
完成对应课时的练习。
解决问题(4)
3
R·六年级上册
一、复习导入
①修路队修一条公路,每天修25m,20天修完,这条公路长多少米
25×20=500(m)
工作效率×工作时间=工作总量
②修路队修一条500m的公路,20天修完,平均每天修多少米
500÷20=25(m)
工作总量÷工作时间=工作效率
③修路队修一条500m的公路,每天修25 m,多少天能修完
500÷25=20(天)
工作总量÷工作效率=工作时间
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
二、探索新知
(教材P40例7)
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
阅读与理解
知道了两个队单独修完需要的时间,要求的是_______________________
两队合修,需要的时间。
这条路有多长呢?
能不能假设知道这条路有多长呢?
可以假设这条道路长18km。
我假设这条道路长30km。
你准备假设这条道路有多长呢?自己试一试,算一算。
甲队每天修:___________________________________
乙队每天修:___________________________________
两队合修,每天修:_____________________________
两队合修,需要多少天:_________________________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有18km。
根据假设的这条路的长度,请你列式计算。
甲队每天修:________________
乙队每天修:________________
两队合修,每天修:___________________
两队合修,需要多少天:_______________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有30km。
根据假设的这条路的长度,请你列式计算。
甲队每天修:________________
乙队每天修:________________
两队合修,每天修:___________________
两队合修,需要多少天:_______________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路是1。
根据假设的这条路的长度,请你列式计算。
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有18km。
假设这条道路有30km。
假设这条道路是1。
不同的方法计算出的结果一样吗?
怎样才知道以上的解决方法是否正确? 把你的想法写下来,和同学交流一下。
回顾与反思
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1,很简便。
答:如果两队合修, 天可以修完。
一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物?
(教材P41“做一做”)
把这批货物看作“1”
答:两辆车一起运,2次能运完这批货物。
1. 挖一条水渠,王伯伯每天能挖整条水渠的 ,李叔叔每天能挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
三、巩固提高
“1”
(教材P42“练习九” 第6题)
2.甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,相向而行,几小时后相遇
答: 小时后相遇。
(教材P42“练习九” 第7题)
3.某水库准备打开泄洪口调节水位。只打开A口,8小时可以完成任务;只打开B口,6小时可以完成任务。如果两个泄洪口同时打开,几小时可以完成任务
答: 小时可以完成任务。
(教材P43“练习九” 第8题)
4.植树队要种300棵树。甲队单独种,种完需要8天;乙队单独种,种完需要10天。现在两队合种,5天能种完吗?
答:现在两队合种,5天能种完。
(教材P43“练习九” 第9题)
四、课堂小结
说一说,怎样解决这类工程问题?
把工作总量看作“1”--工作总量÷效率和=合作时间
五、课后作业
完成对应课时的练习。
单元复习提升
3
R·六年级上册
分 数 除 法
分数除法计算
解决问题
倒数的认识
分数除以整数
分数除以分数
分数除法混合运算
已知一个数的几分之几是多少,求这个数
已知比一个数多或少几分之几是多少,求这个数
和倍问题
工程问题
1.找出下面各数的倒数。
0.6
怎么找一个数的倒数?
找分数的倒数:
把分子和分母颠倒位置。
找小数的倒数:
先把小数化成分数,再求这个分数的倒数。
找带分数的倒数:
先把带分数化成假分数,再求这个
假分数的倒数。
2.计算下列各题。
除以一个数(0除外),等于乘这个数的倒数。
3.计算下列各题。
分数四则混合运算与整数四则
混合运算的运算顺序相同。
①郑和新村栽种柳树和槐树共108棵,其中柳树的棵树
是槐树的 。柳树和槐树各栽了多少棵?
答:槐树栽了60棵,柳树栽了48棵。
解:设槐树栽了x棵,则柳树载了 棵。
108-60=48(棵)
4.解决问题。
②公园的园丁栽了2500盆杜鹃花,比种植的月季花少 ,
种植了多少盆月季花?
答:种植了3125盆月季花。
解:设种植了 x 盆月季花。
③一项工程,甲单独完成需要24天,是乙单独完成天数的 。两人合作,几天可以完成这项工程?
解:设乙单独完成需要 x 天。
x = 24
x = 30
1 ÷( + )= (天)
答: 天可以完成这项工程。
完成对应课时的练习。
课后作业
整理和复习
3
R·六年级上册
一、复习巩固
1.计算下列各题。
怎样计算分数除法?本单元的内容和分数乘法的内容有什么关系?
除以一个数(0 除外),就等于 乘这个数的倒数。
(教材P44“整理和复习” 第1题)
在计算时,分数除法是转化成分数乘法来计算的。在解决本单元的实际问题时,有一部分也是利用分数乘法的数量关系来思考的。
整数可以看成分母是 1的分数,所以不管被除数、除数是整数还是分数,计算方法都是一样的。
1.计算下列各题。
(教材P44“整理和复习” 第1题)
1.计算下列各题。
(教材P44“整理和复习” 第1题)
分数四则运算的顺序和整数是一样的。
2. (1)张大爷养了200只鹅,鹅的数量是鸭的 。张大爷养了多少只鸭
(2)张大爷养了200只鹅,鹅的数量比鸭少 。张大爷养了多少只鸭
(3)张大爷养的鹅和鸭共有700只,其中鹅的数量是鸭的 。鹅和鸭各有多少只
解:设鸭有x只,则鹅有 只。
鹅: 。
答:鸭有500只,鹅有200只。
(教材P44“整理和复习” 第2题)
二、巩固提高
1.计算下列各题。
1.计算下列各题。
2.冰融化成水后,水的体积是冰的体积的 。现有一块冰,融化成水以后的体积是27 dm3,这块冰的体积是多少立方分米
答:这块冰的体积是 30 立方分米。
(教材P45“练习十” 第3题)
3.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢 。猎豹奔跑时的最高速度是多少
答:猎豹奔跑的最高速度是110千米/时。
(教材P45“练习十” 第4题)
4.小莉买了一支圆珠笔和一支钢笔,共用去12元,圆珠笔的单价是钢笔的 。圆珠笔和钢笔的单价各是多少元
解:设钢笔的单价是x元,则圆珠笔单价是 元。
圆珠笔单价:
答:圆珠笔的单价是3元,钢笔单价是9元。
5.小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后首次相遇
答: 分钟后首次相遇。
(教材P45“练习十” 第5题)
答:40分钟后小明超出爷爷一整圈。
5.小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(2)*如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈
五、课后作业
完成对应课时的练习。
倒数的认识
3
R·六年级上册 第三单元 分数除法
文字里有趣的变化!
一、新课导入
呆—杏 音—昱
吞—吴 甲—由
数学里也有这样有趣的变化!
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
相乘的两个数的分子、分母正好颠倒了位置。
这几个算式的乘积都是1
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
乘积是1的两个数互为倒数。
和 互为倒数,就是指 的倒数是 , 的倒数是 。
(1)
+ =1,所以
和 互为倒数 。( )
(2)
× × = 1 ,所以
,
,
互为倒数 。( )
(3)
× =1,所以
是倒数 。( )
×
×
×
(4)
与 的乘积为1,所以
和 互为倒数 。( )
下面的说法对不对,为什么?
√
先计算,再观察,看看有什么规律。
二、探索新知
=1
=1
=1
=1
想一想:互为倒数的两个数有什么特点?
你是怎样找一个数的倒数的?
下面哪两个数互为倒数?
6
1
0
分子、分母交换位置
分子、分母交换位置
6 的倒数是
的倒数是
分子、分母交换位置
的倒数是
1的倒数是多少?0有倒数吗?和同学交流一下你的想法。
1×1=1 1的倒数是1。0乘任何数都得0,0没有倒数。
1.将互为倒数的两个数用线连起来。
三、巩固提高
(教材P28“练习六” 第1题)
2.写出下面各数的倒数。
三、巩固提高
的倒数是 ;
的倒数是 ;
的倒数是 ;
的倒数是 ;
1.25
的倒数是 ;
1.25的倒数是 。
5
4
(教材P27 做一做)
3.填空。
(1)
(2)( )的倒数是它本身,( )没有倒数。
(3) 的倒数是( ),9的倒数是( ),2.5的倒数是( )。
4.先计算出每组算式的结果,再在 里填上“>”“<”或“=”。
=
=
=
(教材P28“练习六” 第4题)
四、课堂小结
通过今天的学习你有什么收获?
乘积是1的两个数互为倒数。
五、课后作业
完成对应课时的练习。
分数除以整数
3
R·六年级上册
一、复习导入
1.说出下面各数的倒数。
4
5
1
7
1
4
5
3
2
1
一、复习导入
2.计算下列各题。
1.5×3
2.3×4
=4.5
=9.2
4.5÷3
9.2÷4
=1.5
=2.3
比较两组算式,你有什么发现?
除法是乘法的逆运算。
二、探索新知
1.探究分数除法的意义。
(1)每盒水果糖重 kg,3盒有多重
(2)3盒水果糖重 kg,每盒有多重
分数除法与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
二、探索新知
怎样列式计算呢?
你能在图中表示出结果吗?
2.探究分数除以整数的计算方法。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
把 平均分成2份,就是把4个 平均分成2份,每份是2个 ,就是 。
把一张纸的 平均分成2份,每份是这张纸的几分之几?
把 平均分成2份,每份就是 的 ,也就是 。
思考:把这张纸的 平均分成3份,每份是这张纸的多少?
___×___=___
说一说,这里把÷3写成× 后再计算,你是怎样想的?
把 平均分成3份,就是求 的 。
根据上面的折纸实验和算式,你能发现什么规律?
分数除以整数(0除外)等于分数乘这个整数的倒数。
1.计算下面各题。
9
10
3
1
10
3
3
8
2
1
3
16
三、巩固提高
×
(教材P29“做一做” )
2.先算出乘法算式的得数,再根据左右两题之间的关系,写出除法算式的得数。
3.小芳将长 m的丝带剪成同样长的8段,每段丝带有多长
答:每段丝带有 米。
(教材P33“练习七” 第2题)
4.填一填。
(教材P33“练习七” 第3题)
分数除以整数(0除外)等于分数乘这个整数的倒数。
四、课堂小结
分数除法与整数除法的意义相同,都是已知两个因数的积与其中一个因数,求另一个因数的运算。
五、课后作业
完成对应课时的练习。
一个数除以分数
3
R·六年级上册
1.一辆汽车2小时行驶90千米,平均每小时行驶多少千米?
一、复习导入
2.计算下面各题,直接写出答案。
速度=路程÷时间
90÷2=45(千米/时)
分数除以整数(0除外)等于分数乘这个整数的倒数。
二、探索新知
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
怎么计算呢? 画个图试试吧。
先求 小时走的千米数,也就是求2km的 ,即
3个 小时走的千米数也就是1小时走的千米数,再乘3,即
1
1
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
所以小明走得快些。
1
1
1
1
2
1
3km>2km
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
通过上面的计算,你发现了什么?你会用自己的方式表示你发现的规律吗?
小明 小时走了2km,小红 小时走了 km。谁走得快些?
小明平均每小时走:
小红平均每小时走:
除以一个不等于0的数,等于乘这个数的倒数。
甲数÷乙数(0除外)=甲数×乙数的倒数
1.计算下面各题。
9
8
27
×
7
16
5
4
×
三、巩固提高
(教材P31“做一做”第1题)
2.计算下面各题。
(教材P31“做一做” 第2题)
3.不用计算,你知道下面哪几道题的商大于被除数、哪几道题的商小于被除数吗
商小于被除数的:
商大于被除数的:
(教材P31“做一做” 第3题)
4.计算下面各题。
(教材P33“练习七” 第4题)
5.把 L橙汁分装在容量是 L的小瓶里,可以装满几瓶
答:可以装满3瓶。
(教材P33“练习七” 第5题)
甲数÷乙数(0除外)=甲数×乙数的倒数
四、课堂小结
一个数除以分数
整数除以分数
分数除以分数
=3
除以一个不等于0的数,等于乘这个数的倒数。
五、课后作业
完成对应课时的练习。
分数混合运算
3
R·六年级上册
说出运算顺序,不用计算。
(18+7)×4 88+30÷5 350-25×2 60÷(77-65)
①
②
一、复习导入
①同级运算,按从左往右的运算顺序进行计算
②两级运算,先算乘法或除法再算加法或减法
③有括号的要先算括号里面的
二、探索新知
一盒药共12片,每次吃半片,每天吃3次。这盒药可以吃几天?
片
一盒药共12片,每次吃半片,每天吃3次。这盒药可以吃几天?
我先算每天吃多少片。
我先算这盒药可以吃几次。
也可以用综合算式表示以上过程,自己试着计算一下。
分数四则运算的顺序和整数一样。
说一说,你是按怎样的顺序计算的?
1.计算下面各题。
(教材P32“做一做”第1题 )
2.一块梯形的玻璃,上底、下底和高分别是
这块玻璃的面积是多少?
( + )× ÷2
5
3
5
4
4
3
答:这块玻璃的面积是 m2 。
= × ×
5
7
4
3
2
1
= (m2)
40
21
(教材P32“做一做”第2题 )
1. 计算下面各题。
三、巩固提高
(教材P34“练习七” 第8题)
2. 李爷爷每天慢跑6圈,他跑半圈大约用2分钟。照这个速度,李爷爷每天慢跑大约要用多少时间?
答:李爷爷每天慢跑大约要用24分钟。
(教材P34“练习七” 第9题)
3.一幢楼共有15 层(如右图)。小萍家住7 楼,她家的地板离地面有多高?
答:小萍家的地板离地20m。
(教材P34“练习七” 第10题)
10
1
2
3
四、课堂小结
分数四则运算的计算顺序和整数四则运算顺序一样。
五、课后作业
完成对应课时的练习。
练习课(第1~3课时)
3
R·六年级上册
一、复习巩固
关于分数除法,你知道了什么
如果两个数的乘积是1,那么这两个数互为倒数,且其中一个数是另一个数的倒数。
1的倒数是1,0没有倒数。
除以一个不为0的数,等于乘这个数的倒数。
分数四则混合运算与整数四则混合运算的运算顺序相同。
二、基础练习
1.填一填。
求一个因数,要用积除以另一个因数。分数除法的意义与整数除法相同。
2.计算下面各题。
(教材P34“练习七” 第12题)
2.计算下面各题。
(教材P34“练习七” 第12题)
3.某饮料厂使用一种自动检测仪检测饮料瓶是否有缺陷,检测一个瓶子所用的时间为 秒。1分钟可以检测多少个瓶子
1分=60秒
答:1分钟可以检测1500个瓶子。
(教材P33“练习七” 第6题)
4.我们平时看到的电影画面实际上是由许多连续拍摄的照片以每 秒一张的速度连续播放的。请你算一算:半秒可以播放多少张照片? 1 分钟呢?
1分=60秒
答:半秒可以播放12张照片,1分钟可以播放1440张照片。
(教材P33“练习七” 第7题)
三、综合练习
1.有240 kg水果糖需要装袋,每袋装 kg,已经装完了总量的 。装完了多少袋?
答:装完了720袋。
(教材P34“练习七” 第11题)
2.解下列方程。
(教材P34“练习七” 第13题)
2.解下列方程。
(教材P34“练习七” 第13题)
3. 一盏节能灯1小时耗电 千瓦时,某个传达室除了这盏节能灯外,没有别的电器。这个传达室上个月的用电量是 千瓦时,这盏灯上个月共使用了多少小时
答:这盏灯上个月共使用了100小时。
(教材P34“练习七” 第14题)
4. 某种手机的自动化生产线在手机机板上插入每个零件的时间仅为 秒。3分钟可以插入多少个零件
3分=180秒
答:3分钟可以插入2000个零件。
(教材P34“练习七” 第15题)
四、拓展练习
按下面的步骤计算,再把最后的得数与开始的数比较,你能发现什么 你知道为什么吗
=
2
3
×
3
4
×
2
1
×
1
1
1
1
=
1
五、课后作业
完成对应课时的练习。
解决问题(1)
3
R·六年级上册
一、复习导入
找出单位“1”,并列出数量关系式。
(1)每把椅子的价钱相当于每张桌子的价钱的 。
5
4
“1”
每张桌子的价钱 × =每把椅子的价钱
5
4
(2)男生人数是女生人数的 。
7
6
“1”
女生人数 × =男生人数
7
6
单位“1”的量×对应的分率=对应的量
二、探索新知
阅读与理解
小明体内的水分重 _______。
小明体内的水分占体重的 ____。
要求的是小明的______。
28kg
体重
(教材P35例4)
分析与解答
水分28kg
体重?kg
水分占体重的
根据“儿童体内的水分占体重的 ”可以列出下面的关系式。
小明的体重× =小明体内水分的质量
分析与解答
水分28kg
体重?kg
水分占体重的
小明的体重× =小明体内水分的质量
解:设小明的体重是x千克。
回顾与反思
看结果是不是小明体内水分的质量。
答:小明的体重是35kg。
28
回顾与反思
解决“已知一个数的几分之几是多少,求这个数”的问题,一般方法:
1.找出单位“1”,设未知量为 x;
2.找出题中的数量关系式;
3.列出方程并解答;
4.检验并写出答案。
小明的体重× =小明体内水分的质量
答:小明的体重是35kg。
分析与解答
水分28kg
体重?kg
水分占体重的
小明的体重× =小明体内水分的质量
28 ÷ = 28× = 35(kg)
5
4
4
5
答:小明的体重是 35 kg。
三、巩固提高
1.我国幅员辽阔,东西相距约5200km,东西距离是南北的 。南北相距约多少千米?
(教材P37“练习八” 第1题)
南北距离× =东西距离
解:设南北相距约x千米。
x=5200
x=5200÷
55
52
x=5200×
52
55
x=5500
答:南北相距约5500千米。
2.一杯250mL的鲜牛奶大约含有 g的钙质,占一个成年人一天所需钙质的 。一个成年人一天大约需要多少钙质
答:一个成年人一天大约需要 g钙质。
(教材P37“练习八” 第2题)
成人一天所需钙质的质量× = g的钙质
解:设一个成年人一天大约需要xg的钙质。
x=
x= ÷
8
3
x=
3.神舟十号载人飞船在轨飞行约15 天,相当于神舟十三号载人飞船在轨飞行时间的 。神舟十三号载人飞船在轨飞行约多少天?
答:神舟十三号载人飞船在轨飞行约183天。
神舟十三号在轨飞行的天数× =神舟十号在轨飞行的天数
(教材P37“练习八” 第3题)
四、课堂小结
明确数量关系—确定单位“1” —列式解答。
28÷ =28× =35(kg)
5
4
4
5
五、课后作业
完成对应课时的练习。
解决问题(2)
3
R·六年级上册
一只大熊猫的寿命约为20年,相当于大猩猩的 。大猩猩的寿命约是多少年
答:大猩猩的寿命约是50年。
一、新课导入
解:设大猩猩的寿命约是x年。
x=20
x=20÷
5
2
x=50
5
2
大猩猩的寿命× =大熊猫的寿命
5
2
二、探索新知
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
阅读与理解
小明的体重是_______。
小明的体重比爸爸轻______。
要求的是___________的体重。
35kg
小明爸爸
(教材P36例5)
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
该怎么画线段图?
爸爸:
小明:
35kg
小明的体重比爸爸轻
是爸爸的体重的几分之几?
?kg
爸爸的体重×(1- )=小明的体重
爸爸的体重-小明比爸爸轻的部分=小明的体重
解:设小明爸爸的体重是xkg。
35÷(1- )=75(kg)
爸爸的体重×(1- )=小明的体重
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
解:设小明爸爸的体重是xkg。
爸爸的体重-小明比爸爸轻的部分=小明的体重
答:小明爸爸的体重是75千克。
分析与解答
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
(75-35 )÷75 =
答:小明爸爸的体重是75kg。
看看小明是否比爸爸轻 。
回顾与反思
小明的体重是35 kg,他的体重比爸爸的体重轻 。小明爸爸的体重是多少千克
解决“已知比一个数多(少)几分之几是多少,求这个数”的问题的一般方法:
1.找出单位“1”。
2.写出题中的数量关系式。
3.列式或者列方程解答。
4.检验并写出答案。
35÷(1- )=75(千克)
答:小明爸爸的体重是75千克。
1.写出题中的等量关系式。
(1)红花有20朵,比黄花多 ,黄花有多少朵?
(2)一批货物,运走了 ,还剩下 t,这批货物重多少吨?
黄花的朵数+黄花朵数× =红花的朵数
原货物质量-原货物质量× = t
三、巩固提高
解:设爸爸每月的工资为x元。
答:爸爸每月的工资为3125元。
2.妈妈每月的工资是2500元,比爸爸的工资少 。
爸爸每月的工资是多少元?
3.小东读一本课外读物,已经读了35页,还剩下 没有读。这本课外读物一共有多少页
解:设这本课外读物一共有x页。
(教材P38“练习八” 第7题)
x=35
x=35÷
x=35×
x=49
答:这本课外读物一共有49页。
4.运送一批大米,运了4车才运走 。平均每车运走这批大米的几分之几 剩下的大米还要几车才能运完
答:平均每车运走这批大米的 ,剩下的大米还要10车才能运完。
(教材P38“练习八” 第9题)
5.有一组互相咬合的齿轮。
(1)大齿轮有140个齿,小齿轮的齿数是大齿轮的 。小齿轮有多少个齿
答:小齿轮有28个齿。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(2) 小齿轮有28个齿,是大齿轮的 。大齿轮有多少个齿
答:大齿轮有140个齿。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(3)小齿轮每分钟转400周,大齿轮每分钟转的周数比小齿轮少 。大齿轮每分钟转多少周
答:大齿轮每分钟转80周。
(教材P38“练习八” 第10题)
5.有一组互相咬合的齿轮。
(4)大齿轮每分钟转80周,比小齿轮每分钟转的周数少 。小齿轮每分钟转多少周
答:小齿轮每分钟转400周。
小齿轮每分钟转的周数×(1- )=大齿轮每分钟转的周数
(教材P40“练习八” 第10题)
四、课堂小结
说一说,我们是怎样解决问题的?
1.找出单位“1”。
2.写出题中的数量关系式。
3.列式或者列方程解答。
4.检验并写出答案。
五、课后作业
完成对应课时的练习。
解决问题(3)
3
R·六年级上册
一、新课导入
计算下面各题。
六年级举行篮球比赛。六(1)班全场得了42 分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
二、探索新知
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
阅读与理解
知道了全场得分_______
下半场得分是上半场得分的____。
42分
求上半场和下半场的得分各是多少。
分析与解答
解:设上半场得了x分,则下半场得了 x分。
下半场得分: (分)
上半场得分+下半场得分=42分
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
也可以想成上半场的得分是下半场的2倍。
还可以怎么做呢?
分析与解答
解:设下半场得了x分,则上半场得了2x分。
上半场得分: 14×2=28(分)
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
28+14=42,全场得分确实是42分。
14÷28= ,下半场得分确实是上半场的一半。
答:上半场得28分,下半场得14分。
回顾与反思
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
回顾与反思
确定数量关系--设单位“1”的量为x,另一个量用含有x的式子表示--列方程解答
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
1.小丽和小华共收集了36张邮票,小丽收集的张数
是小华的3倍。小丽和小华各收集了多少张邮票?
解:设小华收集了x张邮票,则小丽收集了3x张邮票。
x+3x=36
4x=36
x=9
小丽收集的邮票:3×9=27(张)
答:小丽收集了27张邮票,小华收集了9张。
三、巩固提高
2.某电视机厂去年全年生产电视机108万台,其中上半年产量是下半年的 。这个电视机厂去年上半年和下半年的产量分别是多少万台
解:设下半年产量是x万台,则上半年产量是 万台。
答:上半年产量为48万台,下半年产量为60万台。
(教材P42“练习九” 第1题)
3.武汉长江大桥全长约1670m,其中引桥的长度是正桥的 。这座大桥的正桥和引桥的长度
分别是多少米
解:设大桥正桥的长度为x米,则引桥的长度为 米。
答:大桥正桥的长度为1156米,则引桥的长度为514米。
(教材P42“练习九” 第4题)
4.中国二十四节气中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天,北京的黑夜时长是白昼时长的 。白昼和黑夜分别是多少小时
解:设这一天北京白昼为x小时,则黑夜为 小时。
答:这一天北京白昼为15小时,黑夜为9小时。
(教材P42“练习九” 第5题)
四、课堂小结
说一说,怎样列方程解决求2个未知数的问题?
确定数量关系--设单位“1”的量为x,另一个量用含有x的式子表示--列方程解答
六年级举行篮球比赛。六(1)班全场得了42分,其中下半场得分是上半场的一半。六(1)班上半场和下半场各得多少分?
五、课后作业
完成对应课时的练习。
解决问题(4)
3
R·六年级上册
一、复习导入
①修路队修一条公路,每天修25m,20天修完,这条公路长多少米
25×20=500(m)
工作效率×工作时间=工作总量
②修路队修一条500m的公路,20天修完,平均每天修多少米
500÷20=25(m)
工作总量÷工作时间=工作效率
③修路队修一条500m的公路,每天修25 m,多少天能修完
500÷25=20(天)
工作总量÷工作效率=工作时间
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
二、探索新知
(教材P40例7)
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
阅读与理解
知道了两个队单独修完需要的时间,要求的是_______________________
两队合修,需要的时间。
这条路有多长呢?
能不能假设知道这条路有多长呢?
可以假设这条道路长18km。
我假设这条道路长30km。
你准备假设这条道路有多长呢?自己试一试,算一算。
甲队每天修:___________________________________
乙队每天修:___________________________________
两队合修,每天修:_____________________________
两队合修,需要多少天:_________________________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有18km。
根据假设的这条路的长度,请你列式计算。
甲队每天修:________________
乙队每天修:________________
两队合修,每天修:___________________
两队合修,需要多少天:_______________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有30km。
根据假设的这条路的长度,请你列式计算。
甲队每天修:________________
乙队每天修:________________
两队合修,每天修:___________________
两队合修,需要多少天:_______________
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路是1。
根据假设的这条路的长度,请你列式计算。
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。如果两队合修,多少天能修完?
分析与解答
假设这条道路有18km。
假设这条道路有30km。
假设这条道路是1。
不同的方法计算出的结果一样吗?
怎样才知道以上的解决方法是否正确? 把你的想法写下来,和同学交流一下。
回顾与反思
不管假设这条道路有多长,答案都是相同的。把道路长度假设成1,很简便。
答:如果两队合修, 天可以修完。
一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物?
(教材P41“做一做”)
把这批货物看作“1”
答:两辆车一起运,2次能运完这批货物。
1. 挖一条水渠,王伯伯每天能挖整条水渠的 ,李叔叔每天能挖整条水渠的 。两人合作,几天能挖完?
答:两人合作,12天能挖完。
三、巩固提高
“1”
(教材P42“练习九” 第6题)
2.甲车从A城市到B城市要行驶2小时,乙车从B城市到A城市要行驶3小时。两车同时分别从A城市和B城市出发,相向而行,几小时后相遇
答: 小时后相遇。
(教材P42“练习九” 第7题)
3.某水库准备打开泄洪口调节水位。只打开A口,8小时可以完成任务;只打开B口,6小时可以完成任务。如果两个泄洪口同时打开,几小时可以完成任务
答: 小时可以完成任务。
(教材P43“练习九” 第8题)
4.植树队要种300棵树。甲队单独种,种完需要8天;乙队单独种,种完需要10天。现在两队合种,5天能种完吗?
答:现在两队合种,5天能种完。
(教材P43“练习九” 第9题)
四、课堂小结
说一说,怎样解决这类工程问题?
把工作总量看作“1”--工作总量÷效率和=合作时间
五、课后作业
完成对应课时的练习。
单元复习提升
3
R·六年级上册
分 数 除 法
分数除法计算
解决问题
倒数的认识
分数除以整数
分数除以分数
分数除法混合运算
已知一个数的几分之几是多少,求这个数
已知比一个数多或少几分之几是多少,求这个数
和倍问题
工程问题
1.找出下面各数的倒数。
0.6
怎么找一个数的倒数?
找分数的倒数:
把分子和分母颠倒位置。
找小数的倒数:
先把小数化成分数,再求这个分数的倒数。
找带分数的倒数:
先把带分数化成假分数,再求这个
假分数的倒数。
2.计算下列各题。
除以一个数(0除外),等于乘这个数的倒数。
3.计算下列各题。
分数四则混合运算与整数四则
混合运算的运算顺序相同。
①郑和新村栽种柳树和槐树共108棵,其中柳树的棵树
是槐树的 。柳树和槐树各栽了多少棵?
答:槐树栽了60棵,柳树栽了48棵。
解:设槐树栽了x棵,则柳树载了 棵。
108-60=48(棵)
4.解决问题。
②公园的园丁栽了2500盆杜鹃花,比种植的月季花少 ,
种植了多少盆月季花?
答:种植了3125盆月季花。
解:设种植了 x 盆月季花。
③一项工程,甲单独完成需要24天,是乙单独完成天数的 。两人合作,几天可以完成这项工程?
解:设乙单独完成需要 x 天。
x = 24
x = 30
1 ÷( + )= (天)
答: 天可以完成这项工程。
完成对应课时的练习。
课后作业
整理和复习
3
R·六年级上册
一、复习巩固
1.计算下列各题。
怎样计算分数除法?本单元的内容和分数乘法的内容有什么关系?
除以一个数(0 除外),就等于 乘这个数的倒数。
(教材P44“整理和复习” 第1题)
在计算时,分数除法是转化成分数乘法来计算的。在解决本单元的实际问题时,有一部分也是利用分数乘法的数量关系来思考的。
整数可以看成分母是 1的分数,所以不管被除数、除数是整数还是分数,计算方法都是一样的。
1.计算下列各题。
(教材P44“整理和复习” 第1题)
1.计算下列各题。
(教材P44“整理和复习” 第1题)
分数四则运算的顺序和整数是一样的。
2. (1)张大爷养了200只鹅,鹅的数量是鸭的 。张大爷养了多少只鸭
(2)张大爷养了200只鹅,鹅的数量比鸭少 。张大爷养了多少只鸭
(3)张大爷养的鹅和鸭共有700只,其中鹅的数量是鸭的 。鹅和鸭各有多少只
解:设鸭有x只,则鹅有 只。
鹅: 。
答:鸭有500只,鹅有200只。
(教材P44“整理和复习” 第2题)
二、巩固提高
1.计算下列各题。
1.计算下列各题。
2.冰融化成水后,水的体积是冰的体积的 。现有一块冰,融化成水以后的体积是27 dm3,这块冰的体积是多少立方分米
答:这块冰的体积是 30 立方分米。
(教材P45“练习十” 第3题)
3.狮子奔跑时的最高速度可以达到60千米/时,比猎豹奔跑时的最高速度慢 。猎豹奔跑时的最高速度是多少
答:猎豹奔跑的最高速度是110千米/时。
(教材P45“练习十” 第4题)
4.小莉买了一支圆珠笔和一支钢笔,共用去12元,圆珠笔的单价是钢笔的 。圆珠笔和钢笔的单价各是多少元
解:设钢笔的单价是x元,则圆珠笔单价是 元。
圆珠笔单价:
答:圆珠笔的单价是3元,钢笔单价是9元。
5.小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(1)如果两人同时同地出发,相背而行,多少分钟后首次相遇
答: 分钟后首次相遇。
(教材P45“练习十” 第5题)
答:40分钟后小明超出爷爷一整圈。
5.小明和爷爷一起去操场散步。小明走一圈需要8分钟,爷爷走一圈需要10分钟。
(2)*如果两人同时同地出发,同方向而行,多少分钟后小明超出爷爷一整圈
五、课后作业
完成对应课时的练习。
