高中物理教科版(2019)必修一课件 1.5.1 速度变化的快慢与方向——加速度(一)(共23张PPT)
文档属性
| 名称 | 高中物理教科版(2019)必修一课件 1.5.1 速度变化的快慢与方向——加速度(一)(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-09 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第一章 描述运动的基本概念
速度变化的快慢与方向——加速度
6
为什么战斗机速度那么快,起跑却跑不过摩托车呢?
速度变化量
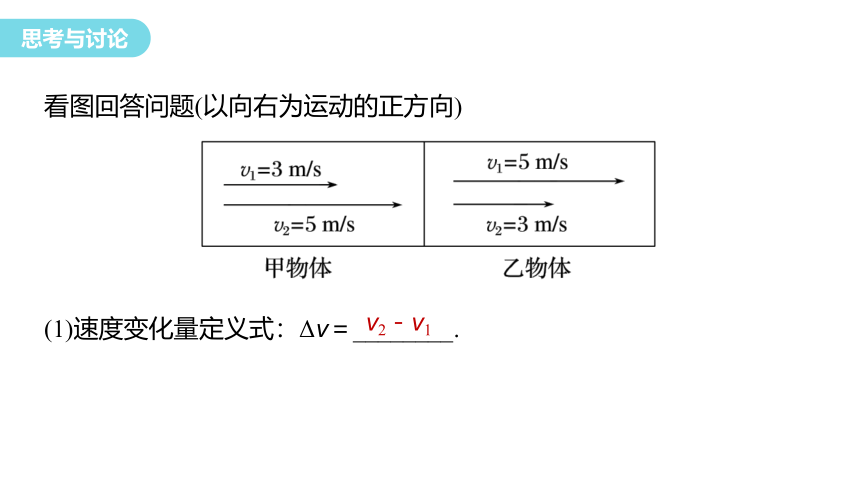
看图回答问题(以向右为运动的正方向)
(1)速度变化量定义式:Δv=________.
v2-v1
(2)请分别把甲物体和乙物体的速度变化量在图中表示出来,并写出数据.
答案
(3)两物体的速度变化量相同吗?你能得到什么结论?
不相同,两物体速度变化量大小相等、方向不同,变化量有方向为矢量,可以用速度变化量的正负表示它的方向。Δv为正表示与规定的正方向相同;Δv为负表示与规定的正方向相反。
(1)速度变化量的方向一定与速度方向相同。( )
(2)速度大小不变,则速度变化量一定为零。( )
×
×
1.下列说法正确的是
A.速度是矢量,速度的变化量是标量
B.甲物体的速度变化量为3 m/s,乙物体的速度变化量为-5 m/s,甲物体
的速度变化量大
C.一小球以10 m/s的速度与墙相撞,弹回时速度大小也为10 m/s,小球的
速度变化量的大小为20 m/s
D.一汽车以10 m/s的速度开始刹车,一段时间后速度变为2 m/s,则汽车
的速度变化量为8 m/s
√
加速度
不同物体的运动速度往往不相同,同一物体的运动快慢也常常是变化的。下表列举了几个物体的运动速度的变化情况.填写下表,并讨论哪个物体的速度变化得最快?说出你判断的依据:
A.自行车下坡 B.公共汽车出站 C.某舰艇出航 D.火车出站
初速度v1/(m·s-1) 2 0 0 0
所用时间t/s 3 3 20 100
末速度v2/(m·s-1) 7 6 6 20
A、B时间t相同,大,则B的速度变化快
速度的变化量v/(m·s-1) ______ ____ ____ ____
速度的变化率 /(m·s-2) _______ ____ ____ ____
5
6
6
20
2
0.3
0.2
B、C相同,时间t短,则B的速度变化快
公共汽车的速度变化得最快
C、D不同, 不同,C的 大,C速度变化快
加速度
1.定义:速度的改变量Δv与发生这一改变所用时间Δt的比。
2.定义式:a=____。其中Δv表示速度的变化量,a在数值上等于单位时
间内速度变化量的大小。
3.物理意义:表示速度变化快慢的物理量。
4.单位:在国际单位制中,加速度的单位是米每二次方秒,符号是m/s2或m·s-2。
某位同学根据a= 得出“物体的加速度a与速度变化量Δv成正比,与时间Δt成反比”的结论,他的结论是否正确?为什么?
(1)物体的速度越大,加速度一定越大。( )
(2)物体速度变化量越大,加速度一定越大。( )
(3)速度很大的物体,其加速度有可能很小,但不能为零。( )
(4)加速度很大时,物体运动的速度可能很小。( )
×
×
√
×
2.(多选)(2022·广东佛山市南海区联考)对下列运动情景中加速度的判断正确的是
A.运动的汽车在某时刻速度为零,故加速度一定为零
B.轿车紧急刹车,速度变化很快,所以加速度很大
C.高速行驶的磁悬浮列车,速度很大,但加速度不一定很大
D.点火后即将升空的火箭,速度很小,其加速度一定也很小
√
√
Δ
v
v1
v2
Δv
v1
v2
(1) v2>v1,则汽车做加速直线运动
(2)v2a
a
1.一辆汽车做直线运动,原来的速度是v1,经过一小段时间Δt后,速度变为v2,试在图中标出速度变化Δv的方向及加速度的方向。
理解加速度方向与速度的变化量方向的关系
2.两物体的加速度分别是-15 m/s2和5 m/s2,哪个加速度大?为什么?阅读“一些运动物体的加速度”表格中的数据,进一步理解负号的意义。
表 一些运动物体的加速度(近似值)
运动物体 a/(m·s-2) 运动物体 a/(m·s-2)
子弹在枪筒中 5×104 赛车起步 4.5
伞兵着陆 -25 汽车起步 2
汽车急刹车 -5 高铁起步 0.35
-15 m/s2大;加速度是矢量,负号说明方向与所选的正方向相反,而不是代数上的正负数,所以是-15 m/s2大。
(1)加速度是矢量,它的方向与速度的变化量Δv的方向一定相同.
(2)在直线运动中,加速度方向与初速度方向相同时,物体做加速直线运动.加速度方向与初速度方向相反时,物体做减速直线运动.当a=0时,v不随时间发生变化,物体做匀速运动.
加速度的方向
3.(多选)下列关于加速度的说法中正确的是
A.加速度方向一定与速度方向相同
B.加速度方向可能与速度方向相反
C.加速度方向与速度变化量方向相反
D.物体的加速度与速度同向时,其速度一定增加
√
√
速度v、速度变化量Δv与加速度a的比较
物理量 速度v 速度变化量Δv 加速度a
物理 意义 表示物体运动的快慢和方向 表示物体速度变化的大小和方向 表示物体速度变化的快慢和方向
定义 位移与所用时间的比值 末速度与初速度的差值 速度变化量与所用时间的比值
表达式 Δv=v2-v1
方向 与Δx的方向相同 由初、末速度决定 与Δv的方向相同
联系 三者无必然联系。速度v很大,速度变化量Δv可能很小,甚至为0,加速度a也可大可小
4.足球运动员在罚点球时,设脚与球的作用时间为0.1 s,若球获得30 m/s的速度并做匀速直线运动,又在空中飞行0.3 s后被守门员挡出,守门员双手与球接触时间为0.1 s,且球被挡出后以10 m/s的速度沿原路弹回,求:
(1)罚点球的瞬间,球的加速度的大小;
(2)守门员接触球的瞬间,球的加速度。
答案 (1) 300 m/s2
(2) 加速度的大小为400 m/s2 ,方向与球被踢出时的方向相反
加速度的计算方法
1.规定正方向。一般选初速度v1的方向为正方向。
2.判定v2的方向,确定v2的符号。
加速度建立的进阶过程
v=Δx/Δt
Δv= v2-v1
a=Δv/Δt
描述运动快慢
描述速度变化
物理意义:描述物体速度变化快慢
单 位:m/s2 方向:a 与 Δv 方向相同
由a与v的方向关系判定物体运动性质
a与v同向,物体做加速运动
a与v反向,物体做减速运动
认知进阶过程
Δv 可能为正也能为负
第一章 描述运动的基本概念
速度变化的快慢与方向——加速度
6
为什么战斗机速度那么快,起跑却跑不过摩托车呢?
速度变化量
看图回答问题(以向右为运动的正方向)
(1)速度变化量定义式:Δv=________.
v2-v1
(2)请分别把甲物体和乙物体的速度变化量在图中表示出来,并写出数据.
答案
(3)两物体的速度变化量相同吗?你能得到什么结论?
不相同,两物体速度变化量大小相等、方向不同,变化量有方向为矢量,可以用速度变化量的正负表示它的方向。Δv为正表示与规定的正方向相同;Δv为负表示与规定的正方向相反。
(1)速度变化量的方向一定与速度方向相同。( )
(2)速度大小不变,则速度变化量一定为零。( )
×
×
1.下列说法正确的是
A.速度是矢量,速度的变化量是标量
B.甲物体的速度变化量为3 m/s,乙物体的速度变化量为-5 m/s,甲物体
的速度变化量大
C.一小球以10 m/s的速度与墙相撞,弹回时速度大小也为10 m/s,小球的
速度变化量的大小为20 m/s
D.一汽车以10 m/s的速度开始刹车,一段时间后速度变为2 m/s,则汽车
的速度变化量为8 m/s
√
加速度
不同物体的运动速度往往不相同,同一物体的运动快慢也常常是变化的。下表列举了几个物体的运动速度的变化情况.填写下表,并讨论哪个物体的速度变化得最快?说出你判断的依据:
A.自行车下坡 B.公共汽车出站 C.某舰艇出航 D.火车出站
初速度v1/(m·s-1) 2 0 0 0
所用时间t/s 3 3 20 100
末速度v2/(m·s-1) 7 6 6 20
A、B时间t相同,大,则B的速度变化快
速度的变化量v/(m·s-1) ______ ____ ____ ____
速度的变化率 /(m·s-2) _______ ____ ____ ____
5
6
6
20
2
0.3
0.2
B、C相同,时间t短,则B的速度变化快
公共汽车的速度变化得最快
C、D不同, 不同,C的 大,C速度变化快
加速度
1.定义:速度的改变量Δv与发生这一改变所用时间Δt的比。
2.定义式:a=____。其中Δv表示速度的变化量,a在数值上等于单位时
间内速度变化量的大小。
3.物理意义:表示速度变化快慢的物理量。
4.单位:在国际单位制中,加速度的单位是米每二次方秒,符号是m/s2或m·s-2。
某位同学根据a= 得出“物体的加速度a与速度变化量Δv成正比,与时间Δt成反比”的结论,他的结论是否正确?为什么?
(1)物体的速度越大,加速度一定越大。( )
(2)物体速度变化量越大,加速度一定越大。( )
(3)速度很大的物体,其加速度有可能很小,但不能为零。( )
(4)加速度很大时,物体运动的速度可能很小。( )
×
×
√
×
2.(多选)(2022·广东佛山市南海区联考)对下列运动情景中加速度的判断正确的是
A.运动的汽车在某时刻速度为零,故加速度一定为零
B.轿车紧急刹车,速度变化很快,所以加速度很大
C.高速行驶的磁悬浮列车,速度很大,但加速度不一定很大
D.点火后即将升空的火箭,速度很小,其加速度一定也很小
√
√
Δ
v
v1
v2
Δv
v1
v2
(1) v2>v1,则汽车做加速直线运动
(2)v2
a
1.一辆汽车做直线运动,原来的速度是v1,经过一小段时间Δt后,速度变为v2,试在图中标出速度变化Δv的方向及加速度的方向。
理解加速度方向与速度的变化量方向的关系
2.两物体的加速度分别是-15 m/s2和5 m/s2,哪个加速度大?为什么?阅读“一些运动物体的加速度”表格中的数据,进一步理解负号的意义。
表 一些运动物体的加速度(近似值)
运动物体 a/(m·s-2) 运动物体 a/(m·s-2)
子弹在枪筒中 5×104 赛车起步 4.5
伞兵着陆 -25 汽车起步 2
汽车急刹车 -5 高铁起步 0.35
-15 m/s2大;加速度是矢量,负号说明方向与所选的正方向相反,而不是代数上的正负数,所以是-15 m/s2大。
(1)加速度是矢量,它的方向与速度的变化量Δv的方向一定相同.
(2)在直线运动中,加速度方向与初速度方向相同时,物体做加速直线运动.加速度方向与初速度方向相反时,物体做减速直线运动.当a=0时,v不随时间发生变化,物体做匀速运动.
加速度的方向
3.(多选)下列关于加速度的说法中正确的是
A.加速度方向一定与速度方向相同
B.加速度方向可能与速度方向相反
C.加速度方向与速度变化量方向相反
D.物体的加速度与速度同向时,其速度一定增加
√
√
速度v、速度变化量Δv与加速度a的比较
物理量 速度v 速度变化量Δv 加速度a
物理 意义 表示物体运动的快慢和方向 表示物体速度变化的大小和方向 表示物体速度变化的快慢和方向
定义 位移与所用时间的比值 末速度与初速度的差值 速度变化量与所用时间的比值
表达式 Δv=v2-v1
方向 与Δx的方向相同 由初、末速度决定 与Δv的方向相同
联系 三者无必然联系。速度v很大,速度变化量Δv可能很小,甚至为0,加速度a也可大可小
4.足球运动员在罚点球时,设脚与球的作用时间为0.1 s,若球获得30 m/s的速度并做匀速直线运动,又在空中飞行0.3 s后被守门员挡出,守门员双手与球接触时间为0.1 s,且球被挡出后以10 m/s的速度沿原路弹回,求:
(1)罚点球的瞬间,球的加速度的大小;
(2)守门员接触球的瞬间,球的加速度。
答案 (1) 300 m/s2
(2) 加速度的大小为400 m/s2 ,方向与球被踢出时的方向相反
加速度的计算方法
1.规定正方向。一般选初速度v1的方向为正方向。
2.判定v2的方向,确定v2的符号。
加速度建立的进阶过程
v=Δx/Δt
Δv= v2-v1
a=Δv/Δt
描述运动快慢
描述速度变化
物理意义:描述物体速度变化快慢
单 位:m/s2 方向:a 与 Δv 方向相同
由a与v的方向关系判定物体运动性质
a与v同向,物体做加速运动
a与v反向,物体做减速运动
认知进阶过程
Δv 可能为正也能为负
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
