7.3多边形内角和
图片预览




文档简介
课件14张PPT。多边形的内角和各式各样的建筑多边形的内角和在前面我们都了解了哪些多边形的内角和? 解:任意的三角形的内角和是180°; 对于四边形来说,我们都知道长方形和正方形的内角和都是360° 任意四边形的内角和又是多少度呢?你怎么得到呢?你能找到几种方法?多边形的内角和P方法总结:
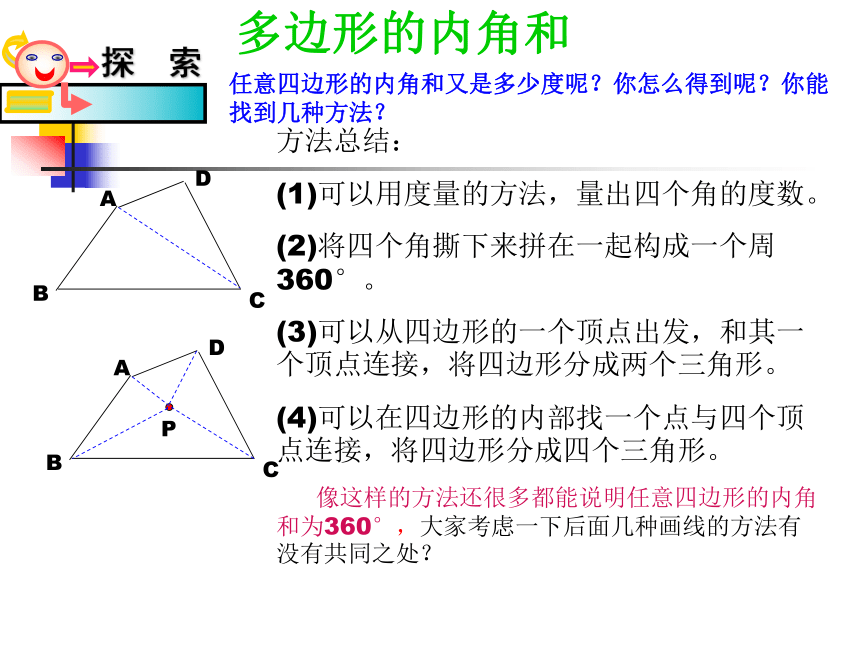
(1)可以用度量的方法,量出四个角的度数。
(2)将四个角撕下来拼在一起构成一个周360°。
(3)可以从四边形的一个顶点出发,和其一个顶点连接,将四边形分成两个三角形。
(4)可以在四边形的内部找一个点与四个顶点连接,将四边形分成四个三角形。
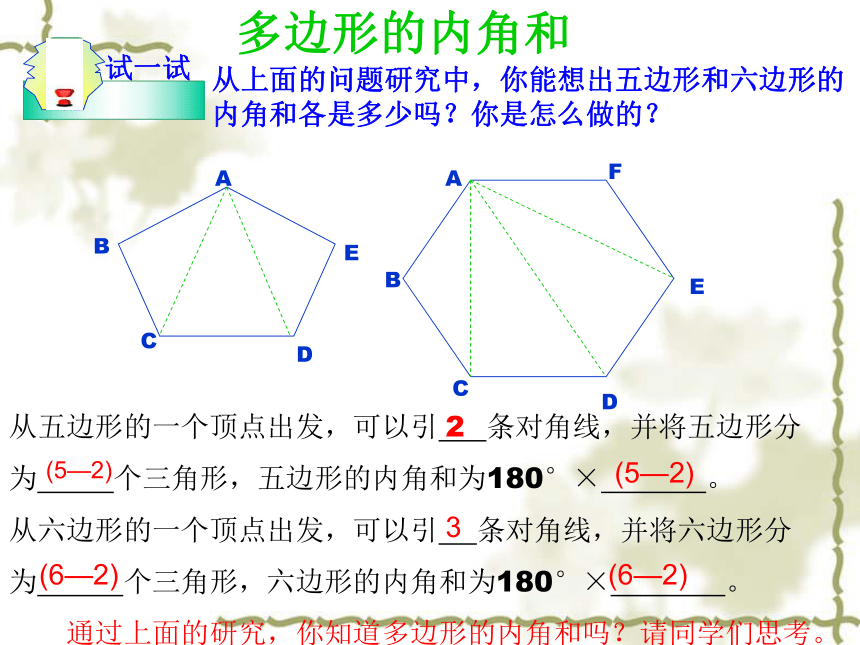
像这样的方法还很多都能说明任意四边形的内角和为360°,大家考虑一下后面几种画线的方法有没有共同之处?多边形的内角和从上面的问题研究中,你能想出五边形和六边形的内角和各是多少吗?你是怎么做的?从五边形的一个顶点出发,可以引 条对角线,并将五边形分
为 个三角形,五边形的内角和为180°× 。
从六边形的一个顶点出发,可以引 条对角线,并将六边形分
为 个三角形,六边形的内角和为180°× 。
通过上面的研究,你知道多边形的内角和吗?请同学们思考。(5—2)(5—2)3(6—2)(6—2)2多边形的内角和(1) 三角形个数与多边形边数有何关系?
三角形个数比多边形的边数 少 2。
(2)多边形的内角和与所有三角形的内角和有何关系?
多边形的内角和与所有三角形的内角和 相等
(3)由此你能得到多边形的内角和吗?
从n边形的一个顶点出发,可以引 条对角线,并将n
边形分为 个三角形, n边形的内角和等于 。
(4)你还有其它的方法可以说明多边形的内角和
为 吗?
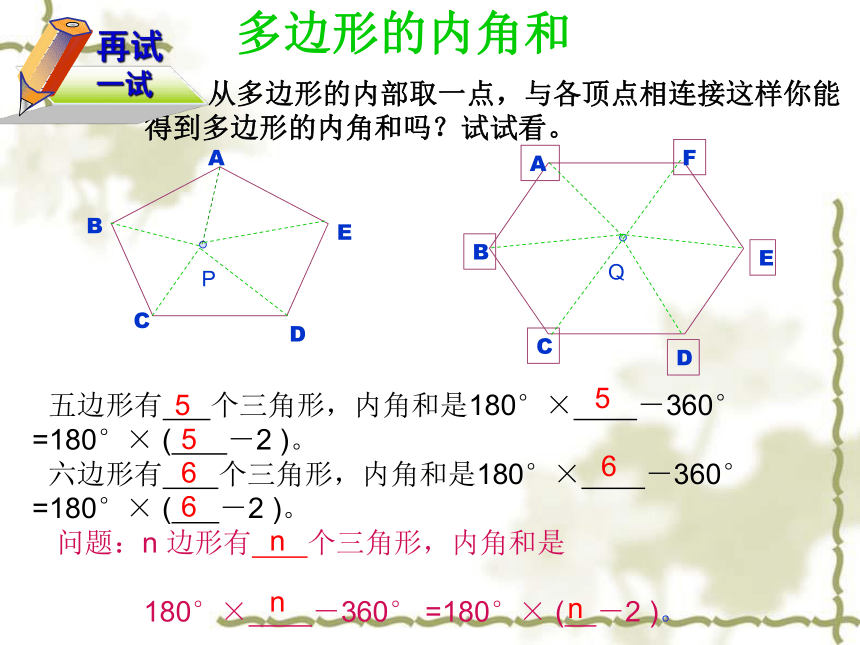
n--3n--2180°×(n—2)180°×(n—2)提问多边形的内角和 从多边形的内部取一点,与各顶点相连接这样你能得到多边形的内角和吗?试试看。PQ 五边形有 个三角形,内角和是180°× -360° =180°× ( -2 )。
六边形有 个三角形,内角和是180°× -360° =180°× ( -2 )。
问题:n 边形有 个三角形,内角和是
180°× -360° =180°× ( -2 )。
555666nnn多边形的内角和说一说你能运用多边形内角和公式解决问题吗?1、说出下列图形中x的值答案:(1)65°(2)60°(3)95°(4)75°多边形的内角和2、快速抢答,熟悉公式(1)、8边形的内角和是 。
(2)、12边形的内角和是 。
(3)、一个多边形的内角和是1440°,它是 边形。
(4)、一个多边形的各内角都等于120°,它是 边形。3、解决问题:如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形ABCD中, ∠A+∠B=180°
因为 ∠A+∠B+∠C+∠D=(4-2)×180°=360°.
所以∠B+∠D=360°-( ∠A+∠C)=360 °-180°=180°.
这就是说,如果四边形的一组对角互补,那么另一 组对角
也互补。1080°1800° 106多边形的外角和等于360°3、如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4,求x的值。1、一个多边形的每个外角都等于60°,它是几边形?2、一个多边形的内角和与外角和相等,它是几边形?多边形的内角和 这节课你有那些收获?
说出来大家分享一下。
1、多边形的内角和为:
(n-2)×180°;
2、已知边数如何求内角和;
3、已知内角和如何求边数。
返回再见
(1)可以用度量的方法,量出四个角的度数。
(2)将四个角撕下来拼在一起构成一个周360°。
(3)可以从四边形的一个顶点出发,和其一个顶点连接,将四边形分成两个三角形。
(4)可以在四边形的内部找一个点与四个顶点连接,将四边形分成四个三角形。
像这样的方法还很多都能说明任意四边形的内角和为360°,大家考虑一下后面几种画线的方法有没有共同之处?多边形的内角和从上面的问题研究中,你能想出五边形和六边形的内角和各是多少吗?你是怎么做的?从五边形的一个顶点出发,可以引 条对角线,并将五边形分
为 个三角形,五边形的内角和为180°× 。
从六边形的一个顶点出发,可以引 条对角线,并将六边形分
为 个三角形,六边形的内角和为180°× 。
通过上面的研究,你知道多边形的内角和吗?请同学们思考。(5—2)(5—2)3(6—2)(6—2)2多边形的内角和(1) 三角形个数与多边形边数有何关系?
三角形个数比多边形的边数 少 2。
(2)多边形的内角和与所有三角形的内角和有何关系?
多边形的内角和与所有三角形的内角和 相等
(3)由此你能得到多边形的内角和吗?
从n边形的一个顶点出发,可以引 条对角线,并将n
边形分为 个三角形, n边形的内角和等于 。
(4)你还有其它的方法可以说明多边形的内角和
为 吗?
n--3n--2180°×(n—2)180°×(n—2)提问多边形的内角和 从多边形的内部取一点,与各顶点相连接这样你能得到多边形的内角和吗?试试看。PQ 五边形有 个三角形,内角和是180°× -360° =180°× ( -2 )。
六边形有 个三角形,内角和是180°× -360° =180°× ( -2 )。
问题:n 边形有 个三角形,内角和是
180°× -360° =180°× ( -2 )。
555666nnn多边形的内角和说一说你能运用多边形内角和公式解决问题吗?1、说出下列图形中x的值答案:(1)65°(2)60°(3)95°(4)75°多边形的内角和2、快速抢答,熟悉公式(1)、8边形的内角和是 。
(2)、12边形的内角和是 。
(3)、一个多边形的内角和是1440°,它是 边形。
(4)、一个多边形的各内角都等于120°,它是 边形。3、解决问题:如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形ABCD中, ∠A+∠B=180°
因为 ∠A+∠B+∠C+∠D=(4-2)×180°=360°.
所以∠B+∠D=360°-( ∠A+∠C)=360 °-180°=180°.
这就是说,如果四边形的一组对角互补,那么另一 组对角
也互补。1080°1800° 106多边形的外角和等于360°3、如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4,求x的值。1、一个多边形的每个外角都等于60°,它是几边形?2、一个多边形的内角和与外角和相等,它是几边形?多边形的内角和 这节课你有那些收获?
说出来大家分享一下。
1、多边形的内角和为:
(n-2)×180°;
2、已知边数如何求内角和;
3、已知内角和如何求边数。
返回再见
