高中物理人教版(2019)选择性必修1课件 2.5 实验:用单摆测量重力加速度(共28张PPT)
文档属性
| 名称 | 高中物理人教版(2019)选择性必修1课件 2.5 实验:用单摆测量重力加速度(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-09 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第二章 机械振动
实验:用单摆测量重力加速度
曾经有个广东(纬度23°)人到瑞士(纬度47°)旅游,看到摆钟很漂亮,就买了一个回家,但是回到广东之后发现摆钟计时不准了,而在瑞士买的时候是很准的。后来就打电话投诉,但经过鉴定摆钟的质量是没有问题的。那问题出现在哪里?摆钟是走慢了还是走快了?如何进行校准呢?
地球上不同地方重力加速度g不同,从瑞士到广东,纬度减小,g变小,摆钟摆动周期变大,摆钟走慢了,应把摆长变短。
T=
根据单摆得周期公式:
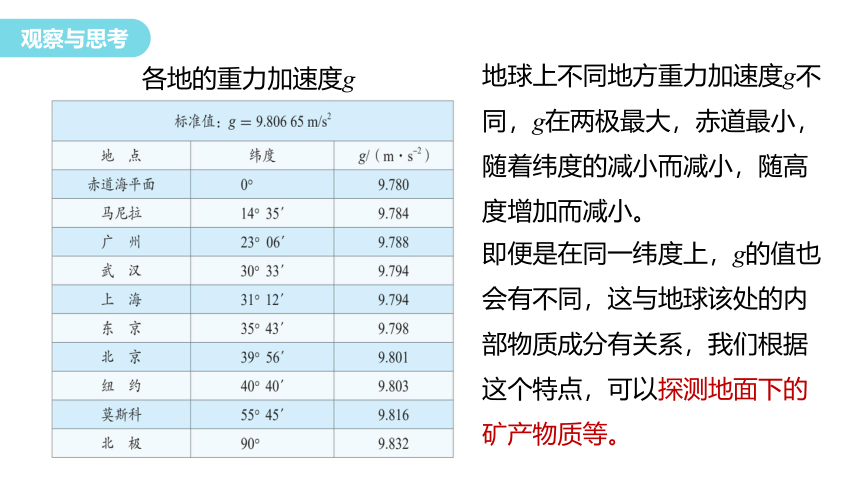
各地的重力加速度g
地球上不同地方重力加速度g不同,g在两极最大,赤道最小,随着纬度的减小而减小,随高度增加而减小。
即便是在同一纬度上,g的值也会有不同,这与地球该处的内部物质成分有关系,我们根据这个特点,可以探测地面下的矿产物质等。
了解地球表面重力加速度的分布,对地球物理学、航空航天技术及大地测量等领域有十分重要的意义。为此,就需要了解测量重力加速度的方法。
地球物理学
航空航天技术
大地测量
自由落体运动法
惠更斯在推导出单摆的周期公式后,用一个单摆测出了巴黎的重力加速度.我们也可以采用同样的办法,测量所在地区的重力加速度数值。
理论上,与重力相关的物理现象都可以用来测量g
单摆法
一、实验思路
1.实验目的
测量重力加速度g
2.实验原理
单摆在偏角很小(小于5°)时的运动,可看成简谐运动,根据其周期
3.物理量的测量
测出摆长l和周期T,即可计算得到当地的重力加速度数值.
T= ,可得g=________.
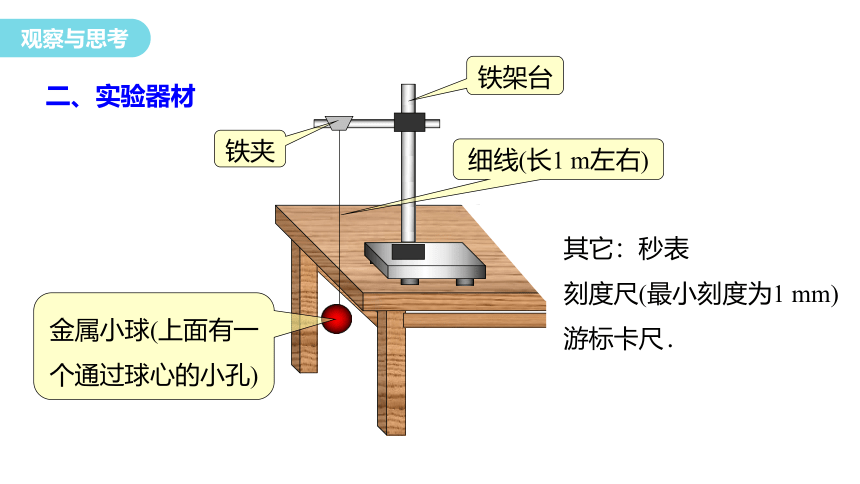
二、实验器材
其它:秒表
刻度尺(最小刻度为1 mm)
游标卡尺.
铁架台
金属小球(上面有一个通过球心的小孔)
铁夹
细线(长1 m左右)
1.做单摆
(1)让细线穿过球上的小孔,在细线的一端打一个比孔稍大一些的线结,制成一个单摆.
(2)将铁夹固定在铁架台上端,铁架台放在实验桌边,把单摆上端固定在铁夹上,使摆线自由下垂.在单摆平衡位置处做上标记.
三、实验步骤
PK
PK
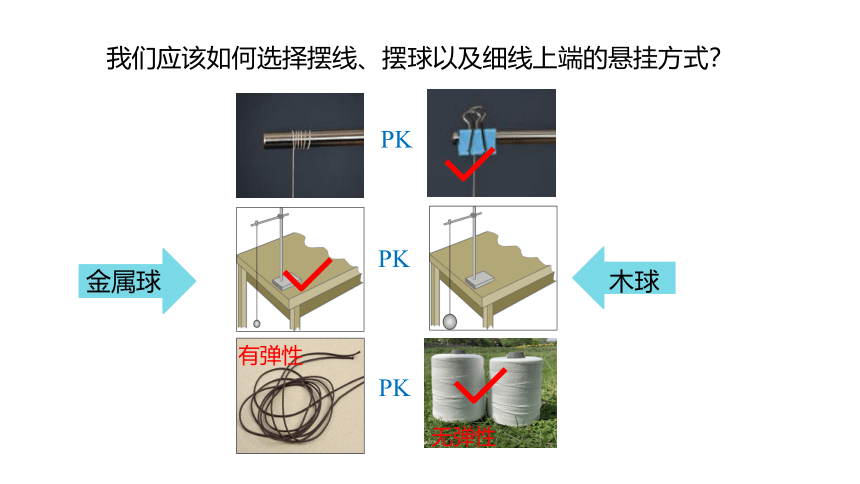
我们应该如何选择摆线、摆球以及细线上端的悬挂方式?
金属球
木球
PK
有弹性
无弹性
2.测摆长
用刻度尺量出悬线长l′(准确到mm),用游标卡尺
测出摆球的直径d,则摆长为l= .
测摆球的直径
累计法测周期:减小误差
4.重复测量
将单摆的摆长变短或变长,重复实验,测出相应的摆长l和周期T.
3.测周期
把单摆从平衡位置拉开一个角度(小于5°),释放摆球。当摆球摆动稳定后,经过最低位置,即平衡位置时,用停表开始计时,测出单摆完成30次(或50次)全振动的时间,求出一次全振动的时间,即为单摆的振动周期。
2分7.6秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
秒表的读数
此时37代表的7
t<2分30秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
1分51.4秒
t>1分30秒
此时读51就代表51
四、数据分析
(1)公式法:每改变一次摆长,将测量数据填入设计好的表格中,把相应的l和T代入g= 中,求出g值,最后求出g的平均值.
实验次数 摆长l/m 周期T/s 重力加速度g/(m·s-2) 重力加速度g的平均值(m·s-2)
1
2
3
五、误差分析
1.误差来源:
本实验系统误差主要来源于单摆模型本身是否符合要求。即:悬点是否固定,球、线是否符合要求,摆动是圆锥摆还是在同一竖直面内的摆动以及测量哪段长度作为摆长等。
本实验偶然误差主要来自时间(即单摆周期)的测量上。
2.误差分析
(1)测量摆长时引起的误差
①若在未悬挂摆球前测量了摆长、摆线拉得过紧、测量了摆线长后却误加了直径等,会使实际的摆长偏小;
②若悬点未固定好,摆球摆动过程中出现松动,测量了摆线长漏加了摆球半径等,使实际的摆长偏大。
(2)测量周期时引起的误差
①由于测量全振动次数错误造成误差。
②开始计时或停止计时时过早或过迟按下停表。
③计量单摆的全振动次数时,不从摆球通过最低点(平衡位置)时开始计时,容易产生较大的计时误差。
六、注意事项
1.选择细而不易被拉长的线,长度一般不应短于1 m;摆球应选用密度较大、直径较小的金属球。
2.单摆悬线的上端应紧夹在铁夹中,不可以随意卷在铁杆上。
3.摆长要悬挂好摆球后再测,不要先测摆长再悬挂小球,不要把摆线长当成摆长。
4.摆动时摆线偏离竖直方向的角度应很小,不能超过5°。
5.摆球摆动时,要使之保持在同一竖直平面内,不要形成圆锥摆。
6.计算单摆的全振动次数时,应从摆球通过最低位置(平衡位置)时开始计时,要测n次全振动的时间t。
1.(2022·盐城市高二期末)用单摆测量重力加速度的实验装置如图甲所示:
(1)组装单摆时,应在下列器材中选用_____(选填选项前的字母)。
A.长度为1 m左右的细线
B.长度为10 cm左右的橡皮绳
C.直径为1.5 cm左右的塑料球
D.直径为1.5 cm左右的铁球
AD
(2)选择好器材,将符合实验要求的单摆挂在铁架台上,应采用图____(选填“乙”或“丙”)所示的固定方式。
丙
(3)下列测量单摆振动周期的方法正确的是_____。
A.把摆球从平衡位置拉开到某一位置,然后由静止释放摆球,在释放摆球
的同时启动停表开始计时,当摆球再次回到原来位置时,按停停表停止
计时
B.以单摆在最大位移处为计时基准位置,用停表测出摆球第n次回到基准位
置的时间t,则T=
C.以摆球在最低位置处为计时基准位置,开始记时后,摆球每经过最低位
置,记数一次,用停表记录摆球n次经过最低位置的时间t,则T=
D.以摆球在最低位置处为计时基准位置,开始记时后,摆球每从同一方向
经过摆球的最低位置记数一次,用停表记录摆球从同一方向n次经过摆球
的最低位置时的时间t,则T=
D
2.(2022·江西丰城九中高二期末)在“用单摆测量重力加速度”的实验中。
(1)某同学先用米尺测得摆线长为97.43 cm,用游标卡尺测得摆球直径如图甲所示为_____ cm,则单摆的摆长为_____ cm;然后用停表记录了单摆振动50次所用的时间如图乙所示为_____ s,则单摆的周期为____ s;当地的重力加速度为g=_____ m/s2;
2.125
98.49
99.8
2.0
9.71
(2)实验中,如果摆球密度不均匀,无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径,具体做法如下:第一次量得悬线长L1,测得振动周期为T1;第二次量得悬线长L2,测得振动周期为T2,由此可
推得重力加速度为g=___________。
(1)造成图线不过坐标原点的原因可能是___________________________。
3.在“用单摆测量重力加速度”的实验中,由单摆做简谐运动的周期公式得到g= ,只要测出多组单摆的摆长l和运动周期T,作出T2-l图像,就可以求出当地的重力加速度。理论上T2-l图线是一条过坐标原点的直线,某同学根据实验数据作出的图像如图所示:
测量摆长时漏掉了摆球的半径
(2)由图像求出的重力加速度g=______ m/s2(取π2=9.87)。
9.87
(3)如果测得的g值偏小,可能的原因是____。
A.测摆长时摆线拉得过紧
B.摆线上端悬点未固定,振动中出现松动,使摆线
长度增加了
C.开始计时时,停表过迟按下
D.实验时误将49次全振动记为50次
B
4.(2023·湖北部分地区高二期末)在“利用单摆测重力加速度”的实验中。
(1)用最小刻度为1 mm的刻度尺测量摆线长,如图甲所示,单摆的摆线长为______ cm;用游标卡尺测量摆球的直径,如图乙所示,则球的直径为_______ cm;
99.15
2.075
(2)实验时用拉力传感器测得摆线的拉力随时间变化的图像,如图丙所示。若用l表示摆长,则重力加速度的表达式为g=_____。
(3)在进行实验数据处理时,甲、乙两位同学把摆线长和小球直径之和作为摆长。甲同学直接利用公式求出各组重力加速度,再求出平均值;乙同学做出T2-l图像后求出斜率,然后算出重力加速度,两同学处理数据的方法对结果的影响是:甲_____,乙___
_____。(均选填“偏大”“偏小”或“无影响”)
偏大
无
影响
实验:用单摆测量重力加速度
二、实验器材
铁架台及铁夹、金属小球、秒表、细线、刻度尺、游标卡尺
一、实验思路
三、实验步骤
1.做单摆 2.测摆长 3.测周期 4.重复实验
四、数据分析
公式法
图像法
平均值法
五、误差分析
系统误差
偶然误差
六、注意事项
T= ,可得g=
第二章 机械振动
实验:用单摆测量重力加速度
曾经有个广东(纬度23°)人到瑞士(纬度47°)旅游,看到摆钟很漂亮,就买了一个回家,但是回到广东之后发现摆钟计时不准了,而在瑞士买的时候是很准的。后来就打电话投诉,但经过鉴定摆钟的质量是没有问题的。那问题出现在哪里?摆钟是走慢了还是走快了?如何进行校准呢?
地球上不同地方重力加速度g不同,从瑞士到广东,纬度减小,g变小,摆钟摆动周期变大,摆钟走慢了,应把摆长变短。
T=
根据单摆得周期公式:
各地的重力加速度g
地球上不同地方重力加速度g不同,g在两极最大,赤道最小,随着纬度的减小而减小,随高度增加而减小。
即便是在同一纬度上,g的值也会有不同,这与地球该处的内部物质成分有关系,我们根据这个特点,可以探测地面下的矿产物质等。
了解地球表面重力加速度的分布,对地球物理学、航空航天技术及大地测量等领域有十分重要的意义。为此,就需要了解测量重力加速度的方法。
地球物理学
航空航天技术
大地测量
自由落体运动法
惠更斯在推导出单摆的周期公式后,用一个单摆测出了巴黎的重力加速度.我们也可以采用同样的办法,测量所在地区的重力加速度数值。
理论上,与重力相关的物理现象都可以用来测量g
单摆法
一、实验思路
1.实验目的
测量重力加速度g
2.实验原理
单摆在偏角很小(小于5°)时的运动,可看成简谐运动,根据其周期
3.物理量的测量
测出摆长l和周期T,即可计算得到当地的重力加速度数值.
T= ,可得g=________.
二、实验器材
其它:秒表
刻度尺(最小刻度为1 mm)
游标卡尺.
铁架台
金属小球(上面有一个通过球心的小孔)
铁夹
细线(长1 m左右)
1.做单摆
(1)让细线穿过球上的小孔,在细线的一端打一个比孔稍大一些的线结,制成一个单摆.
(2)将铁夹固定在铁架台上端,铁架台放在实验桌边,把单摆上端固定在铁夹上,使摆线自由下垂.在单摆平衡位置处做上标记.
三、实验步骤
PK
PK
我们应该如何选择摆线、摆球以及细线上端的悬挂方式?
金属球
木球
PK
有弹性
无弹性
2.测摆长
用刻度尺量出悬线长l′(准确到mm),用游标卡尺
测出摆球的直径d,则摆长为l= .
测摆球的直径
累计法测周期:减小误差
4.重复测量
将单摆的摆长变短或变长,重复实验,测出相应的摆长l和周期T.
3.测周期
把单摆从平衡位置拉开一个角度(小于5°),释放摆球。当摆球摆动稳定后,经过最低位置,即平衡位置时,用停表开始计时,测出单摆完成30次(或50次)全振动的时间,求出一次全振动的时间,即为单摆的振动周期。
2分7.6秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
秒表的读数
此时37代表的7
t<2分30秒
0
31
2
33
4
35
6
37
8
39
41
10
43
12
14
45
16
47
18
49
20
51
22
53
24
26
55
57
28
59
0
1
2
6
7
8
9
10
11
3
4
5
12
13
14
1分51.4秒
t>1分30秒
此时读51就代表51
四、数据分析
(1)公式法:每改变一次摆长,将测量数据填入设计好的表格中,把相应的l和T代入g= 中,求出g值,最后求出g的平均值.
实验次数 摆长l/m 周期T/s 重力加速度g/(m·s-2) 重力加速度g的平均值(m·s-2)
1
2
3
五、误差分析
1.误差来源:
本实验系统误差主要来源于单摆模型本身是否符合要求。即:悬点是否固定,球、线是否符合要求,摆动是圆锥摆还是在同一竖直面内的摆动以及测量哪段长度作为摆长等。
本实验偶然误差主要来自时间(即单摆周期)的测量上。
2.误差分析
(1)测量摆长时引起的误差
①若在未悬挂摆球前测量了摆长、摆线拉得过紧、测量了摆线长后却误加了直径等,会使实际的摆长偏小;
②若悬点未固定好,摆球摆动过程中出现松动,测量了摆线长漏加了摆球半径等,使实际的摆长偏大。
(2)测量周期时引起的误差
①由于测量全振动次数错误造成误差。
②开始计时或停止计时时过早或过迟按下停表。
③计量单摆的全振动次数时,不从摆球通过最低点(平衡位置)时开始计时,容易产生较大的计时误差。
六、注意事项
1.选择细而不易被拉长的线,长度一般不应短于1 m;摆球应选用密度较大、直径较小的金属球。
2.单摆悬线的上端应紧夹在铁夹中,不可以随意卷在铁杆上。
3.摆长要悬挂好摆球后再测,不要先测摆长再悬挂小球,不要把摆线长当成摆长。
4.摆动时摆线偏离竖直方向的角度应很小,不能超过5°。
5.摆球摆动时,要使之保持在同一竖直平面内,不要形成圆锥摆。
6.计算单摆的全振动次数时,应从摆球通过最低位置(平衡位置)时开始计时,要测n次全振动的时间t。
1.(2022·盐城市高二期末)用单摆测量重力加速度的实验装置如图甲所示:
(1)组装单摆时,应在下列器材中选用_____(选填选项前的字母)。
A.长度为1 m左右的细线
B.长度为10 cm左右的橡皮绳
C.直径为1.5 cm左右的塑料球
D.直径为1.5 cm左右的铁球
AD
(2)选择好器材,将符合实验要求的单摆挂在铁架台上,应采用图____(选填“乙”或“丙”)所示的固定方式。
丙
(3)下列测量单摆振动周期的方法正确的是_____。
A.把摆球从平衡位置拉开到某一位置,然后由静止释放摆球,在释放摆球
的同时启动停表开始计时,当摆球再次回到原来位置时,按停停表停止
计时
B.以单摆在最大位移处为计时基准位置,用停表测出摆球第n次回到基准位
置的时间t,则T=
C.以摆球在最低位置处为计时基准位置,开始记时后,摆球每经过最低位
置,记数一次,用停表记录摆球n次经过最低位置的时间t,则T=
D.以摆球在最低位置处为计时基准位置,开始记时后,摆球每从同一方向
经过摆球的最低位置记数一次,用停表记录摆球从同一方向n次经过摆球
的最低位置时的时间t,则T=
D
2.(2022·江西丰城九中高二期末)在“用单摆测量重力加速度”的实验中。
(1)某同学先用米尺测得摆线长为97.43 cm,用游标卡尺测得摆球直径如图甲所示为_____ cm,则单摆的摆长为_____ cm;然后用停表记录了单摆振动50次所用的时间如图乙所示为_____ s,则单摆的周期为____ s;当地的重力加速度为g=_____ m/s2;
2.125
98.49
99.8
2.0
9.71
(2)实验中,如果摆球密度不均匀,无法确定重心位置,一位同学设计了一个巧妙的方法不计摆球的半径,具体做法如下:第一次量得悬线长L1,测得振动周期为T1;第二次量得悬线长L2,测得振动周期为T2,由此可
推得重力加速度为g=___________。
(1)造成图线不过坐标原点的原因可能是___________________________。
3.在“用单摆测量重力加速度”的实验中,由单摆做简谐运动的周期公式得到g= ,只要测出多组单摆的摆长l和运动周期T,作出T2-l图像,就可以求出当地的重力加速度。理论上T2-l图线是一条过坐标原点的直线,某同学根据实验数据作出的图像如图所示:
测量摆长时漏掉了摆球的半径
(2)由图像求出的重力加速度g=______ m/s2(取π2=9.87)。
9.87
(3)如果测得的g值偏小,可能的原因是____。
A.测摆长时摆线拉得过紧
B.摆线上端悬点未固定,振动中出现松动,使摆线
长度增加了
C.开始计时时,停表过迟按下
D.实验时误将49次全振动记为50次
B
4.(2023·湖北部分地区高二期末)在“利用单摆测重力加速度”的实验中。
(1)用最小刻度为1 mm的刻度尺测量摆线长,如图甲所示,单摆的摆线长为______ cm;用游标卡尺测量摆球的直径,如图乙所示,则球的直径为_______ cm;
99.15
2.075
(2)实验时用拉力传感器测得摆线的拉力随时间变化的图像,如图丙所示。若用l表示摆长,则重力加速度的表达式为g=_____。
(3)在进行实验数据处理时,甲、乙两位同学把摆线长和小球直径之和作为摆长。甲同学直接利用公式求出各组重力加速度,再求出平均值;乙同学做出T2-l图像后求出斜率,然后算出重力加速度,两同学处理数据的方法对结果的影响是:甲_____,乙___
_____。(均选填“偏大”“偏小”或“无影响”)
偏大
无
影响
实验:用单摆测量重力加速度
二、实验器材
铁架台及铁夹、金属小球、秒表、细线、刻度尺、游标卡尺
一、实验思路
三、实验步骤
1.做单摆 2.测摆长 3.测周期 4.重复实验
四、数据分析
公式法
图像法
平均值法
五、误差分析
系统误差
偶然误差
六、注意事项
T= ,可得g=
