高中物理人教版(2019)选择性必修1课件 2.4 单摆(共30张PPT)
文档属性
| 名称 | 高中物理人教版(2019)选择性必修1课件 2.4 单摆(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 65.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-09 16:51:05 | ||
图片预览









文档简介
(共30张PPT)
第二章 机械振动
单摆
判天地之美,析万物之理—庄子
单摆及其回复力
游乐大摆锤
风铃
秋千
生活中的摆动
摆钟
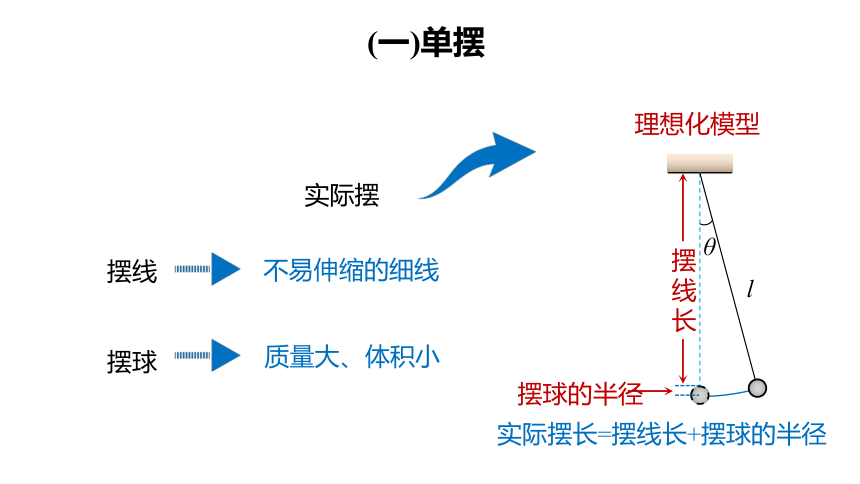
(一)单摆
如果细线的长度不可改变;细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆.
与小球受到的重力及拉线相比,空气等对它的阻力可以忽略.
θ
l
理想化模型
摆线
摆球
实际摆长=摆线长+摆球的半径
摆线长
θ
l
不易伸缩的细线
质量大、体积小
摆球的半径
实际摆
(一)单摆
平衡位置
O
O
A’
A
FT
mg
mgcosθ
mgsinθ
圆弧
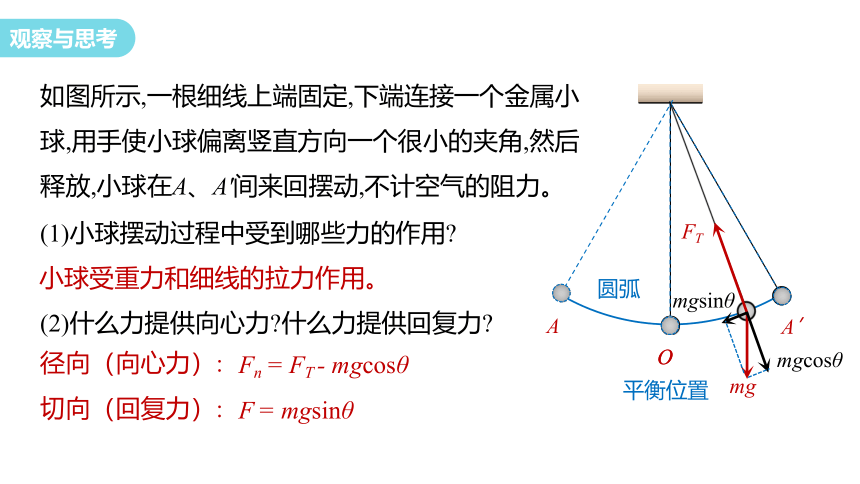
如图所示,一根细线上端固定,下端连接一个金属小球,用手使小球偏离竖直方向一个很小的夹角,然后释放,小球在A、A'间来回摆动,不计空气的阻力。
(1)小球摆动过程中受到哪些力的作用
(2)什么力提供向心力 什么力提供回复力
小球受重力和细线的拉力作用。
F = mgsinθ
Fn = FT - mgcosθ
切向(回复力):
径向(向心力):
平衡位置
O
O
A’
A
FT
mg
mgcosθ
mgsinθ
圆弧
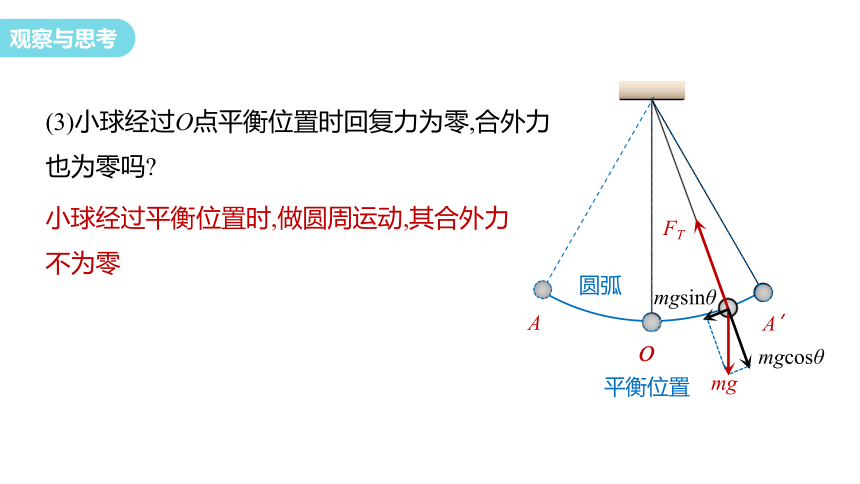
(3)小球经过O点平衡位置时回复力为零,合外力也为零吗
小球经过平衡位置时,做圆周运动,其合外力不为零
平衡位置
O
O
B
A
C
圆弧
x
D
回复力F = mgsinθ
F= - kx
l
夹角θ sinθ 弧度值θ
1° 0.01745 0.01745
2° 0.03490 0.03491
3° 0.05234 0.05236
4° 0.06976 0.06979
5° 0.08716 0.08725
②当 θ 很小时,sinθ≈θ
①当θ 很小时,弧长≈x
当摆角很小时,单摆在竖直面内的摆动可看作是简谐运动.
回复力与位移的方向相反
细线下悬挂一个漏斗,漏斗内装满沙子。当漏斗摆动时,沿着垂直于摆动的方向匀速拖动木板,观察呈现在木板上的沙子图样。
(二)单摆的回复力
(1)来源:摆球的重力沿圆弧切线方向的分力提供回复力.
(2)规律:在摆角很小的情况下,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总是指向平衡位置,即F= . 从回复力特点可以判断单摆做简谐运动.
(1)单摆运动的回复力是重力和摆线拉力的合力。( )
(2)单摆经过平衡位置时受到的合力为零。( )
(3)单摆摆动到最高点时速度为零,合外力也为零。( )
×
×
×
1.(2023·青岛一中月考)图中O点为单摆的固定悬点,现将摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程中
A.摆球受到重力、拉力、回复力三个力的作用
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,速度最大,细线拉力也最大
D.摆球在B点处,速度最大,回复力也最大
√
2.(多选)如图所示为一单摆的振动图像,则
A.t1和t3时刻摆线的拉力等大
B.t2和t3时刻摆球速度相等
C.t3时刻摆球速度正在减小
D.t4时刻摆线的拉力正在减小
√
√
单摆的周期
一条短绳系一个小球,它的振动周期较短。
悬绳较长的秋千,周期较长。
秒摆:用大约1m长的细线栓着小钢球,它的周期大约为2s;
傅科摆:摆长大约67m的傅科摆,它的周期约为16.43s
傅科摆
不同的单摆周期不同,那么单摆的周期与哪些因素有关?
应该采用什么实验方法进行研究?
摆长l、摆球质量m、振幅A
探究方法:控制变量法
研究单摆的振幅、质量、摆长对周期的影响。
现象和结论:两摆同步摆动,说明周期与振幅无关,即摆长和质量相同,振幅不同,周期相同。
单摆的等时性:单摆的周期与振幅无关的性质。
实验一:将摆长相同、质量相同的摆球拉到不同高度(即振幅不同,都在小偏角下)自由释放,观察两摆的摆动情况。
定性研究影响单摆周期的因素
实验二:将摆长相同、质量不同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
现象和结论:两摆同步摆动,说明周期与质量无关,
即:摆长和振幅相同,质量不同,周期相同。
定性研究影响单摆周期的因素
实验三:将摆长不同、质量相同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
现象和结论:两摆不同步摆动,说明周期与摆长有关,
即:振幅和质量相同,摆长不同,周期不同,摆长越长,周期越大。
定性研究影响单摆周期的因素
单摆的周期
1.单摆振动的周期与摆球质量无关,与振幅无关,但与摆长有关,摆长越长,周期越大.
2.(1)提出:单摆周期公式是荷兰物理学家惠更斯首先提出的。
(2)单摆的周期公式T= ,即周期T 与摆长l的二次方根成
正比,与重力加速度g 的二次方根成反比,而与振幅、摆球质量无关.
惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动。请思考:
(1)摆针走时偏快应如何校准?
调节螺母使圆盘沿摆杆下移。
(2)将一个走时准确的摆钟从福建移到北京,摆钟应如何校准?
调节螺母使圆盘沿摆杆下移。
(1)摆球的质量越大,周期越大。( )
(2)若单摆的振幅变为原来的一半,则周期也将变为原来的一半。
( )
×
×
3.(来自教材)周期是2 s的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,它在月球上做50次全振动要用多少时间?已知地球表面的重力加速度为9.8 m/s2,月球上的自由落体加速度为1.6 m/s2,π2取9.8。
B.甲、乙两单摆振动的频率之比是3∶2
C.甲、乙两单摆振动的周期之比是2∶3
D.若甲、乙两单摆在不同地点摆动,但摆长相同,则甲、乙两单摆所在
地点的重力加速度之比为9∶4
4.(多选)(2022·白城市洮南十中月考)甲、乙两个单摆的振动图像如图所示,根据振动图像可以判定
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆
长之比是9∶4
√
√
√
5.如图所示,MN为半径较大的光滑圆弧的一部分,把小球A放在MN的圆心处,再把另一个小球B放在MN上离最低点C很近的B处(弧BC所对圆心角小于5°),今使两小球同时由静止释放,则
A.球A先到达C点
B.球B先到达C点
C.两球同时到达C点
D.无法确定哪个球先到达C点
√
6.如图所示为相同的小球(可看作质点)构成的单摆,所有的绳子长度都相同,在不同的条件下的周期分别为T1、T2、T3、T4(其中(3)图两小球均带负电荷,(4)图中振动系统处于匀加速下降的电梯内),关于周期大小关系的判断,正确的是
A.T1>T2>T3>T4 B.T4C.T4>T1=T3>T2 D.T1√
对l、g的理解
(1)公式中l是摆长,即悬点到摆球球心的距离。
(b)图中,乙在垂直纸面方向摆动时,其等效摆长等于甲摆的摆长;乙在纸面内小角度摆动时,等效摆长等于丙摆的摆长。
(2)①公式中g是单摆所在地的重力加速度,由单摆所在的空间位置决定。
②等效重力加速度:一般情况下,公式中g的值等于摆球静止在平衡位置时,摆线的拉力与摆球质量的比值。
二:单摆的周期
一:单摆及其回复力
单摆
单摆
单摆的回复力
理想化模型
重力沿圆弧切线方向的分力提供
摆角很小时,与位移成正比,指向平衡位置
证明单摆做简谐运动
影响因素
周期公式
惠更斯首次提出
与摆球质量、振幅无关,与摆场有关
等效摆长
等效重力加速度
第二章 机械振动
单摆
判天地之美,析万物之理—庄子
单摆及其回复力
游乐大摆锤
风铃
秋千
生活中的摆动
摆钟
(一)单摆
如果细线的长度不可改变;细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆.
与小球受到的重力及拉线相比,空气等对它的阻力可以忽略.
θ
l
理想化模型
摆线
摆球
实际摆长=摆线长+摆球的半径
摆线长
θ
l
不易伸缩的细线
质量大、体积小
摆球的半径
实际摆
(一)单摆
平衡位置
O
O
A’
A
FT
mg
mgcosθ
mgsinθ
圆弧
如图所示,一根细线上端固定,下端连接一个金属小球,用手使小球偏离竖直方向一个很小的夹角,然后释放,小球在A、A'间来回摆动,不计空气的阻力。
(1)小球摆动过程中受到哪些力的作用
(2)什么力提供向心力 什么力提供回复力
小球受重力和细线的拉力作用。
F = mgsinθ
Fn = FT - mgcosθ
切向(回复力):
径向(向心力):
平衡位置
O
O
A’
A
FT
mg
mgcosθ
mgsinθ
圆弧
(3)小球经过O点平衡位置时回复力为零,合外力也为零吗
小球经过平衡位置时,做圆周运动,其合外力不为零
平衡位置
O
O
B
A
C
圆弧
x
D
回复力F = mgsinθ
F= - kx
l
夹角θ sinθ 弧度值θ
1° 0.01745 0.01745
2° 0.03490 0.03491
3° 0.05234 0.05236
4° 0.06976 0.06979
5° 0.08716 0.08725
②当 θ 很小时,sinθ≈θ
①当θ 很小时,弧长≈x
当摆角很小时,单摆在竖直面内的摆动可看作是简谐运动.
回复力与位移的方向相反
细线下悬挂一个漏斗,漏斗内装满沙子。当漏斗摆动时,沿着垂直于摆动的方向匀速拖动木板,观察呈现在木板上的沙子图样。
(二)单摆的回复力
(1)来源:摆球的重力沿圆弧切线方向的分力提供回复力.
(2)规律:在摆角很小的情况下,摆球所受的回复力与它偏离平衡位置的位移成正比,方向总是指向平衡位置,即F= . 从回复力特点可以判断单摆做简谐运动.
(1)单摆运动的回复力是重力和摆线拉力的合力。( )
(2)单摆经过平衡位置时受到的合力为零。( )
(3)单摆摆动到最高点时速度为零,合外力也为零。( )
×
×
×
1.(2023·青岛一中月考)图中O点为单摆的固定悬点,现将摆球(可视为质点)拉至A点,此时细线处于张紧状态,释放摆球,摆球将在竖直平面内的A、C之间来回摆动,B点为运动中的最低位置,则在摆动过程中
A.摆球受到重力、拉力、回复力三个力的作用
B.摆球在A点和C点处,速度为零,回复力也为零
C.摆球在B点处,速度最大,细线拉力也最大
D.摆球在B点处,速度最大,回复力也最大
√
2.(多选)如图所示为一单摆的振动图像,则
A.t1和t3时刻摆线的拉力等大
B.t2和t3时刻摆球速度相等
C.t3时刻摆球速度正在减小
D.t4时刻摆线的拉力正在减小
√
√
单摆的周期
一条短绳系一个小球,它的振动周期较短。
悬绳较长的秋千,周期较长。
秒摆:用大约1m长的细线栓着小钢球,它的周期大约为2s;
傅科摆:摆长大约67m的傅科摆,它的周期约为16.43s
傅科摆
不同的单摆周期不同,那么单摆的周期与哪些因素有关?
应该采用什么实验方法进行研究?
摆长l、摆球质量m、振幅A
探究方法:控制变量法
研究单摆的振幅、质量、摆长对周期的影响。
现象和结论:两摆同步摆动,说明周期与振幅无关,即摆长和质量相同,振幅不同,周期相同。
单摆的等时性:单摆的周期与振幅无关的性质。
实验一:将摆长相同、质量相同的摆球拉到不同高度(即振幅不同,都在小偏角下)自由释放,观察两摆的摆动情况。
定性研究影响单摆周期的因素
实验二:将摆长相同、质量不同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
现象和结论:两摆同步摆动,说明周期与质量无关,
即:摆长和振幅相同,质量不同,周期相同。
定性研究影响单摆周期的因素
实验三:将摆长不同、质量相同摆球拉到同一高度(振幅相同)自由释放,观察两摆的摆动情况。
现象和结论:两摆不同步摆动,说明周期与摆长有关,
即:振幅和质量相同,摆长不同,周期不同,摆长越长,周期越大。
定性研究影响单摆周期的因素
单摆的周期
1.单摆振动的周期与摆球质量无关,与振幅无关,但与摆长有关,摆长越长,周期越大.
2.(1)提出:单摆周期公式是荷兰物理学家惠更斯首先提出的。
(2)单摆的周期公式T= ,即周期T 与摆长l的二次方根成
正比,与重力加速度g 的二次方根成反比,而与振幅、摆球质量无关.
惠更斯利用摆的等时性发明了带摆的计时器,叫摆钟。摆钟运行时克服摩擦所需的能量由重锤的势能提供,运行的速率由钟摆控制。旋转钟摆下端的螺母可以使摆上的圆盘沿摆杆上下移动。请思考:
(1)摆针走时偏快应如何校准?
调节螺母使圆盘沿摆杆下移。
(2)将一个走时准确的摆钟从福建移到北京,摆钟应如何校准?
调节螺母使圆盘沿摆杆下移。
(1)摆球的质量越大,周期越大。( )
(2)若单摆的振幅变为原来的一半,则周期也将变为原来的一半。
( )
×
×
3.(来自教材)周期是2 s的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,它在月球上做50次全振动要用多少时间?已知地球表面的重力加速度为9.8 m/s2,月球上的自由落体加速度为1.6 m/s2,π2取9.8。
B.甲、乙两单摆振动的频率之比是3∶2
C.甲、乙两单摆振动的周期之比是2∶3
D.若甲、乙两单摆在不同地点摆动,但摆长相同,则甲、乙两单摆所在
地点的重力加速度之比为9∶4
4.(多选)(2022·白城市洮南十中月考)甲、乙两个单摆的振动图像如图所示,根据振动图像可以判定
A.若甲、乙两单摆在同一地点摆动,甲、乙两单摆摆
长之比是9∶4
√
√
√
5.如图所示,MN为半径较大的光滑圆弧的一部分,把小球A放在MN的圆心处,再把另一个小球B放在MN上离最低点C很近的B处(弧BC所对圆心角小于5°),今使两小球同时由静止释放,则
A.球A先到达C点
B.球B先到达C点
C.两球同时到达C点
D.无法确定哪个球先到达C点
√
6.如图所示为相同的小球(可看作质点)构成的单摆,所有的绳子长度都相同,在不同的条件下的周期分别为T1、T2、T3、T4(其中(3)图两小球均带负电荷,(4)图中振动系统处于匀加速下降的电梯内),关于周期大小关系的判断,正确的是
A.T1>T2>T3>T4 B.T4
对l、g的理解
(1)公式中l是摆长,即悬点到摆球球心的距离。
(b)图中,乙在垂直纸面方向摆动时,其等效摆长等于甲摆的摆长;乙在纸面内小角度摆动时,等效摆长等于丙摆的摆长。
(2)①公式中g是单摆所在地的重力加速度,由单摆所在的空间位置决定。
②等效重力加速度:一般情况下,公式中g的值等于摆球静止在平衡位置时,摆线的拉力与摆球质量的比值。
二:单摆的周期
一:单摆及其回复力
单摆
单摆
单摆的回复力
理想化模型
重力沿圆弧切线方向的分力提供
摆角很小时,与位移成正比,指向平衡位置
证明单摆做简谐运动
影响因素
周期公式
惠更斯首次提出
与摆球质量、振幅无关,与摆场有关
等效摆长
等效重力加速度
