人教版九年级上册第24课时 圆的基本性质同步练习(含解析)
文档属性
| 名称 | 人教版九年级上册第24课时 圆的基本性质同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 13:37:39 | ||
图片预览


文档简介
第六单元 圆
第24课时 圆的基本性质
30分钟
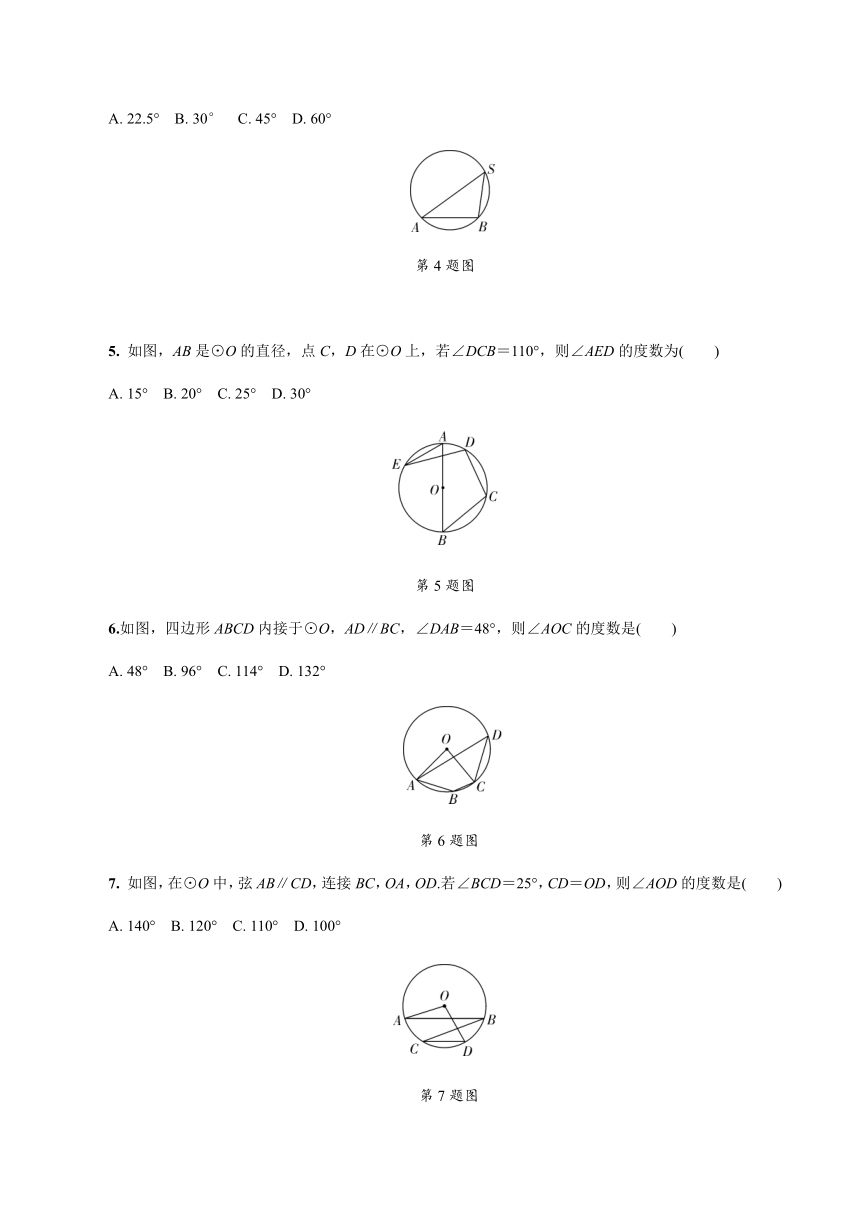
1.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )
A. ∠B B. ∠C C. ∠DEB D. ∠D
第1题图
2. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A. 50° B. 55° C. 60° D. 65°
第2题图
3. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
A. 110° B. 120° C. 135° D. 140°
第3题图
4.如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
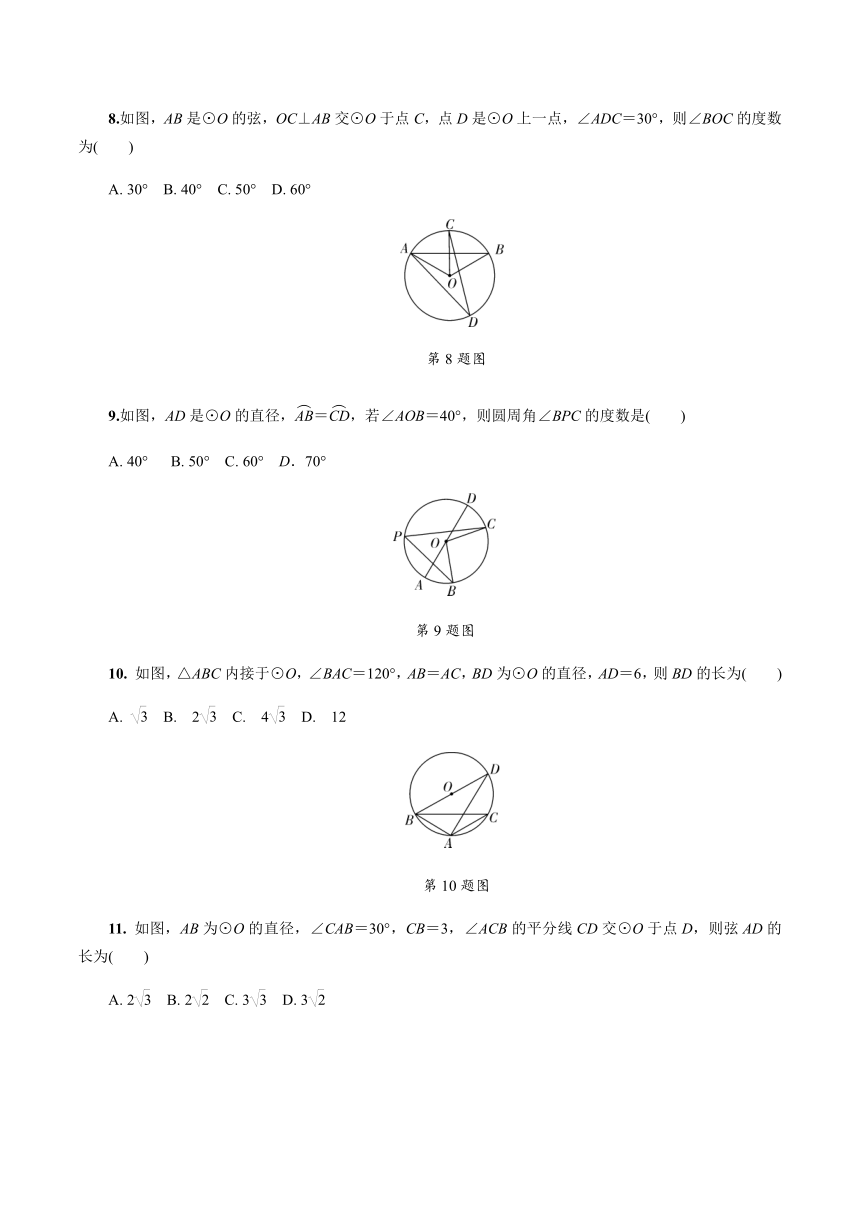
A. 22.5° B. 30° C. 45° D. 60°
第4题图
5. 如图,AB是⊙O的直径,点C,D在⊙O上,若∠DCB=110°,则∠AED的度数为( )
A. 15° B. 20° C. 25° D. 30°
第5题图
6.如图,四边形ABCD内接于⊙O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A. 48° B. 96° C. 114° D. 132°
第6题图
7. 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=25°,CD=OD,则∠AOD的度数是( )
A. 140° B. 120° C. 110° D. 100°
第7题图
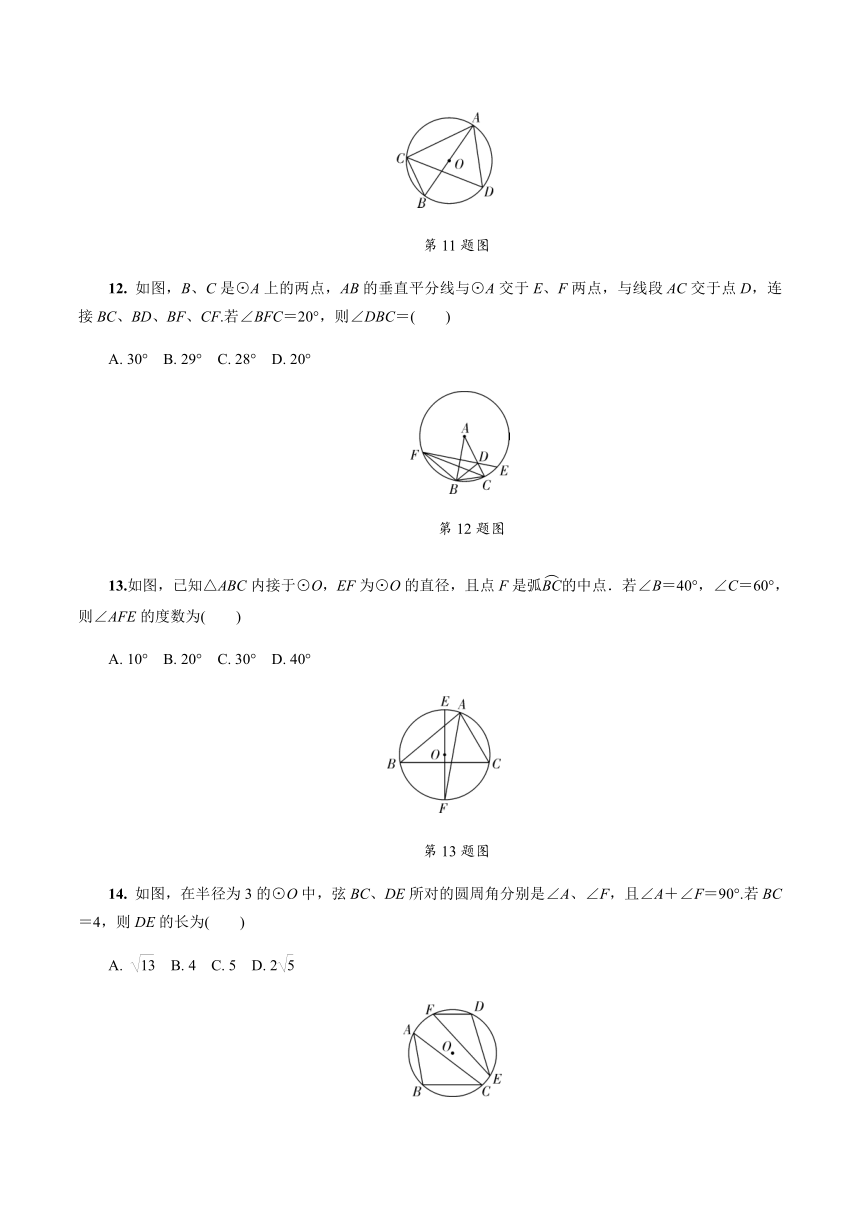
8.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC的度数为( )
A. 30° B. 40° C. 50° D. 60°
第8题图
9.如图,AD是⊙O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是( )
A. 40° B. 50° C. 60° D.70°
第9题图
10. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BD的长为( )
A. B. 2 C. 4 D. 12
第10题图
11. 如图,AB为⊙O的直径,∠CAB=30°,CB=3,∠ACB的平分线CD交⊙O于点D,则弦AD的长为( )
A. 2 B. 2 C. 3 D. 3
第11题图
12. 如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于点D,连接BC、BD、BF、CF.若∠BFC=20°,则∠DBC=( )
A. 30° B. 29° C. 28° D. 20°
第12题图
13.如图,已知△ABC内接于⊙O,EF为⊙O的直径,且点F是弧的中点.若∠B=40°,∠C=60°,则∠AFE的度数为( )
A. 10° B. 20° C. 30° D. 40°
第13题图
14. 如图,在半径为3的⊙O中,弦BC、DE所对的圆周角分别是∠A、∠F,且∠A+∠F=90°.若BC=4,则DE的长为( )
A. B. 4 C. 5 D. 2
第14题图
15. 在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=3,CD=2,则线段CE的长为( )
第15题图
A.
B.
C.
D.
16. 如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD=________度.
第16题图
如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为________.
第17题图
18. 已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是________.
10分钟
1.如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A. AP=2OP B. CD=2OP
C. OB⊥AC D. AC平分OB
第1题图
2. 如图,已知⊙O的内接五边形ABCDE,连接BE、CE,若AB=BC=CE,∠EDC=130°,则∠ABE的度数为( )
A. 25° B. 30° C. 35° D. 40°
第2题图
3. 如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=80°,则∠EAC的度数为( )
A. 20° B. 25°
C. 30° D. 35°
第3题图
4. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为________.
5. 如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心,1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP、OA,则△AOP面积的最大值为________.
第5题图
2分钟
1. 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
第1题图
A. B. 2 C. D.
参考答案
第24课时 圆的基本性质
点对点·课时内考点巩固
1. D 【解析】在⊙O中,∵∠A与∠D都是所对的圆周角,∴∠A=∠D.
2. A 【解析】∵OB=OC,∴∠OCB=∠OBC=40°.∴在△OBC中,∠BOC=180°-∠OCB-∠OBC=180°-40°-40°=100°.∴∠A=∠BOC=×100°=50°.
3. D 【解析】∵四边形ABCD内接于⊙O,∠A=40°,∴∠C=180°-∠A=140°.
4. C 【解析】如解图,设圆心为O,半径为r,则AB=r.连接OA、OB,则r2+r2=(r)2,∴△OAB为等腰直角三角形,∠AOB=90°.∴∠ASB=∠AOB=45°.
第4题解图
5. B 【解析】如解图,连接AC,∵AB为直径,∴∠ACB=90°,∴∠ACD=∠DCB-∠ACB=110°-90°=20°,∴∠AED=∠ACD=20°.
第5题解图
6. B 【解析】∵AD∥BC,∴∠B=180°-∠DAB=132°,∵四边形ABCD内接于⊙O,∴∠D=180°-∠B=48°,由圆周角定理得,∠AOC=2∠D=96°.
7. C 【解析】如解图,连接OC,∵AB∥CD,∴∠B=∠BCD=25°,∴∠AOC=50°,∵CD=OD,OD=OC,∴OC=OD=CD,∴△COD为等边三角形,∴∠COD=60°,∴∠AOD=∠AOC+∠COD=110°.
第7题解图
D 【解析】∵OC⊥AB,∴点C是的中点,即=.∴∠BOC=∠AOC=2∠ADC=60°.
9. B 【解析】∵=,∴∠COD=∠AOB=40°,∴∠BOC=100°,∴∠BPC=∠BOC=50°.
10. C 【解析】∵∠BAC=120°,AB=AC,∴∠BCA=×(180°-120°)=30°.∴∠D=∠BCA=30°.∵BD为⊙O的直径,∴∠BAD=90°.在Rt△BAD中,BD===4.
11. D 【解析】如解图,连接BD,∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,∵∠CAB=30°,∴AB=2CB=6,∵CD平分∠ACB,∴∠BCD=45°,∵∠BAD=∠BCD=45°,∴△ABD为等腰直角三角形,∴AD=AB=×6=3.
第11题解图
12. A 【解析】∵∠BFC=20°,∴∠BAC=2∠BFC=40°,∵AB=AC,∴∠ABC=∠ACB=(180°-40°)=70°.又∵EF是线段AB的垂直平分线,∴AD=BD,∴∠ABD=∠BAC=40°,∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
13. A 【解析】如解图,连接OC、CF.∵∠B=40°,∠ACB=60°,∴∠BAC=80°,∠AFC=∠ABC=40°,∵点F是弧的中点,∴∠BAF=∠CAF=40°,∴∠COF=2∠CAF=80°,∵OF=OC,∴∠OFC=(180°-80°)=50°,∴∠AFE=∠OFC-∠AFC=10°.
第13题解图
14. D 【解析】如解图,连接DO并延长,交⊙O于点G,连接EG、FG,则∠DFG=∠DEG=90°,又∵∠A+∠DFE=90°,∠GFE+∠DFE=90°,∴∠A=∠GFE.则GE=BC=4.∵⊙O的半径为3,∴DG=6.在Rt△DEG中,DE===2.
第14题解图
15. C 【解析】如解图,作BM⊥AC于点M,DN⊥AC于点N,则BM∥DN,∴△BME∽△DNE,∴=,∵∠ACB=∠ACD=60°,∴∠CBM=∠CDN=30°,∴CM=BC=,CN=CD=,∴BM=CM=,DN=CN=,∴MN=CM-CN=,∴=,∴EN=MN=,∴CE=CN+EN=+=.
第15题解图
16. 20 【解析】∵AB为⊙O的直径,点C在⊙O上,且OC⊥AB,∴∠ADC=∠AOC=45°.∵∠AEC=65°,且∠AEC是△ADE的一个外角,∴∠BAD=∠AEC-∠ADC=20°.
17. 【解析】如解图,连接OA、OC,∵∠CBA=45°,∴∠AOC=90°.又∵OA=OC=2,∴AC=2.在Rt△ACD中,∠CDA=90°,∠CAD=30°,∴CD=AC·sin30°=.
第17题解图
18. 105°或15° 【解析】如解图,连接OC,OA,OB.∵OC=OA=AC=5,∴△OAC是等边三角形,∴∠CAO=60°,∵OA=OB=5,AB=5,∴OA2+OB2=AB2,∴△OAB是等腰直角三角形,∠OAB=45°,点C的位置有两种情况,如解图①时,∠BAC=∠CAO+∠OAB=60°+45°=105°;如解图②时,∠BAC=∠CAO-∠OAB=60°-45°=15°.综上所述,∠BAC的度数是105°或15°.
第18题解图
点对线·板块内考点衔接
1. A 【解析】如解图,连接OC.∵四边形OBCD是平行四边形,OD=OB,∴四边形OBCD是菱形.∴OD=OC=CD.∵AD是⊙O的直径,∴∠ACD=90°.∵CD∥OB,∴CD=2OP,OB⊥AC.故B、C选项正确.∵△CBP≌△COP(HL),∴BP=OP.故D选项正确.
第1题解图
2. B 【解析】如解图,连接OA,OB,OC,OE,∵AB=BC=CE,∴==,∠1=∠2=∠3,在四边形BCDE中,∵∠D=130°,∴∠CBE=50°,∠2=2∠CBE=100°,∴∠1=∠3=∠2=100°,∠AOE=360°-3×100°=60°,∴∠ABE=∠AOE=30°.
第2题解图
3. C 【解析】∵∠AEB+∠AEC=∠D+∠AEC=180°,∠D=80°,∴∠AEB=∠D=80°.∵四边形ABCD是菱形,∴∠B=∠D=80°,AB=BC,∴∠B=∠AEB.∴∠BAE=180°-2∠B=20°,∠BAC=∠ACB=(180°-∠B)=50°.∴∠EAC=∠BAC-∠BAE=30°.
4. 5 【解析】如解图,四边形ABCD为正方形,BD为⊙O的直径,OA为半径,则OA=OB=5,OA⊥OB,∴AB= ==5.
第4题解图
5. 【解析】如解图,延长AO至C点,过点D作DF⊥AC于点F,延长FD交⊙D于点P′,连接AP′,OP′,要使△AOP面积最大,则只需AO边上的高最大,此时P′满足条件,即P′F为△AOP的AO边上最大的高.∵DF===,∴P′F=DF+DP′=+1=,AO=AC=,∴△AOP的最大面积为AO·P′F=××=.
第5题解图
点对面·跨板块考点迁移
1. D 【解析】如解图,连接AC、AO,得到等腰三角形AOC,过A点作AD⊥OC,垂足为点D,∴∠CAD=∠CAO=∠OBC,∵点C坐标为(0,2),∴CD=OD=1,∴在Rt△ACD中,AD===2,∴tan∠OBC=tan∠CAD===.
第1题解图
第24课时 圆的基本性质
30分钟
1.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是( )
A. ∠B B. ∠C C. ∠DEB D. ∠D
第1题图
2. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A. 50° B. 55° C. 60° D. 65°
第2题图
3. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
A. 110° B. 120° C. 135° D. 140°
第3题图
4.如图,点A,B,S在圆上,若弦AB的长度等于圆半径的倍,则∠ASB的度数是( )
A. 22.5° B. 30° C. 45° D. 60°
第4题图
5. 如图,AB是⊙O的直径,点C,D在⊙O上,若∠DCB=110°,则∠AED的度数为( )
A. 15° B. 20° C. 25° D. 30°
第5题图
6.如图,四边形ABCD内接于⊙O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A. 48° B. 96° C. 114° D. 132°
第6题图
7. 如图,在⊙O中,弦AB∥CD,连接BC,OA,OD.若∠BCD=25°,CD=OD,则∠AOD的度数是( )
A. 140° B. 120° C. 110° D. 100°
第7题图
8.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC的度数为( )
A. 30° B. 40° C. 50° D. 60°
第8题图
9.如图,AD是⊙O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是( )
A. 40° B. 50° C. 60° D.70°
第9题图
10. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BD的长为( )
A. B. 2 C. 4 D. 12
第10题图
11. 如图,AB为⊙O的直径,∠CAB=30°,CB=3,∠ACB的平分线CD交⊙O于点D,则弦AD的长为( )
A. 2 B. 2 C. 3 D. 3
第11题图
12. 如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于点D,连接BC、BD、BF、CF.若∠BFC=20°,则∠DBC=( )
A. 30° B. 29° C. 28° D. 20°
第12题图
13.如图,已知△ABC内接于⊙O,EF为⊙O的直径,且点F是弧的中点.若∠B=40°,∠C=60°,则∠AFE的度数为( )
A. 10° B. 20° C. 30° D. 40°
第13题图
14. 如图,在半径为3的⊙O中,弦BC、DE所对的圆周角分别是∠A、∠F,且∠A+∠F=90°.若BC=4,则DE的长为( )
A. B. 4 C. 5 D. 2
第14题图
15. 在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=3,CD=2,则线段CE的长为( )
第15题图
A.
B.
C.
D.
16. 如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD=________度.
第16题图
如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为2,则CD的长为________.
第17题图
18. 已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是________.
10分钟
1.如图,AD是⊙O的直径,BC是弦,四边形OBCD是平行四边形,AC与OB相交于点P,下列结论错误的是( )
A. AP=2OP B. CD=2OP
C. OB⊥AC D. AC平分OB
第1题图
2. 如图,已知⊙O的内接五边形ABCDE,连接BE、CE,若AB=BC=CE,∠EDC=130°,则∠ABE的度数为( )
A. 25° B. 30° C. 35° D. 40°
第2题图
3. 如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=80°,则∠EAC的度数为( )
A. 20° B. 25°
C. 30° D. 35°
第3题图
4. 在半径为5的圆形纸片上裁出一个边长最大的正方形纸片,则这个正方形纸片的边长应为________.
5. 如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心,1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP、OA,则△AOP面积的最大值为________.
第5题图
2分钟
1. 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
第1题图
A. B. 2 C. D.
参考答案
第24课时 圆的基本性质
点对点·课时内考点巩固
1. D 【解析】在⊙O中,∵∠A与∠D都是所对的圆周角,∴∠A=∠D.
2. A 【解析】∵OB=OC,∴∠OCB=∠OBC=40°.∴在△OBC中,∠BOC=180°-∠OCB-∠OBC=180°-40°-40°=100°.∴∠A=∠BOC=×100°=50°.
3. D 【解析】∵四边形ABCD内接于⊙O,∠A=40°,∴∠C=180°-∠A=140°.
4. C 【解析】如解图,设圆心为O,半径为r,则AB=r.连接OA、OB,则r2+r2=(r)2,∴△OAB为等腰直角三角形,∠AOB=90°.∴∠ASB=∠AOB=45°.
第4题解图
5. B 【解析】如解图,连接AC,∵AB为直径,∴∠ACB=90°,∴∠ACD=∠DCB-∠ACB=110°-90°=20°,∴∠AED=∠ACD=20°.
第5题解图
6. B 【解析】∵AD∥BC,∴∠B=180°-∠DAB=132°,∵四边形ABCD内接于⊙O,∴∠D=180°-∠B=48°,由圆周角定理得,∠AOC=2∠D=96°.
7. C 【解析】如解图,连接OC,∵AB∥CD,∴∠B=∠BCD=25°,∴∠AOC=50°,∵CD=OD,OD=OC,∴OC=OD=CD,∴△COD为等边三角形,∴∠COD=60°,∴∠AOD=∠AOC+∠COD=110°.
第7题解图
D 【解析】∵OC⊥AB,∴点C是的中点,即=.∴∠BOC=∠AOC=2∠ADC=60°.
9. B 【解析】∵=,∴∠COD=∠AOB=40°,∴∠BOC=100°,∴∠BPC=∠BOC=50°.
10. C 【解析】∵∠BAC=120°,AB=AC,∴∠BCA=×(180°-120°)=30°.∴∠D=∠BCA=30°.∵BD为⊙O的直径,∴∠BAD=90°.在Rt△BAD中,BD===4.
11. D 【解析】如解图,连接BD,∵AB为⊙O的直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,∵∠CAB=30°,∴AB=2CB=6,∵CD平分∠ACB,∴∠BCD=45°,∵∠BAD=∠BCD=45°,∴△ABD为等腰直角三角形,∴AD=AB=×6=3.
第11题解图
12. A 【解析】∵∠BFC=20°,∴∠BAC=2∠BFC=40°,∵AB=AC,∴∠ABC=∠ACB=(180°-40°)=70°.又∵EF是线段AB的垂直平分线,∴AD=BD,∴∠ABD=∠BAC=40°,∴∠DBC=∠ABC-∠ABD=70°-40°=30°.
13. A 【解析】如解图,连接OC、CF.∵∠B=40°,∠ACB=60°,∴∠BAC=80°,∠AFC=∠ABC=40°,∵点F是弧的中点,∴∠BAF=∠CAF=40°,∴∠COF=2∠CAF=80°,∵OF=OC,∴∠OFC=(180°-80°)=50°,∴∠AFE=∠OFC-∠AFC=10°.
第13题解图
14. D 【解析】如解图,连接DO并延长,交⊙O于点G,连接EG、FG,则∠DFG=∠DEG=90°,又∵∠A+∠DFE=90°,∠GFE+∠DFE=90°,∴∠A=∠GFE.则GE=BC=4.∵⊙O的半径为3,∴DG=6.在Rt△DEG中,DE===2.
第14题解图
15. C 【解析】如解图,作BM⊥AC于点M,DN⊥AC于点N,则BM∥DN,∴△BME∽△DNE,∴=,∵∠ACB=∠ACD=60°,∴∠CBM=∠CDN=30°,∴CM=BC=,CN=CD=,∴BM=CM=,DN=CN=,∴MN=CM-CN=,∴=,∴EN=MN=,∴CE=CN+EN=+=.
第15题解图
16. 20 【解析】∵AB为⊙O的直径,点C在⊙O上,且OC⊥AB,∴∠ADC=∠AOC=45°.∵∠AEC=65°,且∠AEC是△ADE的一个外角,∴∠BAD=∠AEC-∠ADC=20°.
17. 【解析】如解图,连接OA、OC,∵∠CBA=45°,∴∠AOC=90°.又∵OA=OC=2,∴AC=2.在Rt△ACD中,∠CDA=90°,∠CAD=30°,∴CD=AC·sin30°=.
第17题解图
18. 105°或15° 【解析】如解图,连接OC,OA,OB.∵OC=OA=AC=5,∴△OAC是等边三角形,∴∠CAO=60°,∵OA=OB=5,AB=5,∴OA2+OB2=AB2,∴△OAB是等腰直角三角形,∠OAB=45°,点C的位置有两种情况,如解图①时,∠BAC=∠CAO+∠OAB=60°+45°=105°;如解图②时,∠BAC=∠CAO-∠OAB=60°-45°=15°.综上所述,∠BAC的度数是105°或15°.
第18题解图
点对线·板块内考点衔接
1. A 【解析】如解图,连接OC.∵四边形OBCD是平行四边形,OD=OB,∴四边形OBCD是菱形.∴OD=OC=CD.∵AD是⊙O的直径,∴∠ACD=90°.∵CD∥OB,∴CD=2OP,OB⊥AC.故B、C选项正确.∵△CBP≌△COP(HL),∴BP=OP.故D选项正确.
第1题解图
2. B 【解析】如解图,连接OA,OB,OC,OE,∵AB=BC=CE,∴==,∠1=∠2=∠3,在四边形BCDE中,∵∠D=130°,∴∠CBE=50°,∠2=2∠CBE=100°,∴∠1=∠3=∠2=100°,∠AOE=360°-3×100°=60°,∴∠ABE=∠AOE=30°.
第2题解图
3. C 【解析】∵∠AEB+∠AEC=∠D+∠AEC=180°,∠D=80°,∴∠AEB=∠D=80°.∵四边形ABCD是菱形,∴∠B=∠D=80°,AB=BC,∴∠B=∠AEB.∴∠BAE=180°-2∠B=20°,∠BAC=∠ACB=(180°-∠B)=50°.∴∠EAC=∠BAC-∠BAE=30°.
4. 5 【解析】如解图,四边形ABCD为正方形,BD为⊙O的直径,OA为半径,则OA=OB=5,OA⊥OB,∴AB= ==5.
第4题解图
5. 【解析】如解图,延长AO至C点,过点D作DF⊥AC于点F,延长FD交⊙D于点P′,连接AP′,OP′,要使△AOP面积最大,则只需AO边上的高最大,此时P′满足条件,即P′F为△AOP的AO边上最大的高.∵DF===,∴P′F=DF+DP′=+1=,AO=AC=,∴△AOP的最大面积为AO·P′F=××=.
第5题解图
点对面·跨板块考点迁移
1. D 【解析】如解图,连接AC、AO,得到等腰三角形AOC,过A点作AD⊥OC,垂足为点D,∴∠CAD=∠CAO=∠OBC,∵点C坐标为(0,2),∴CD=OD=1,∴在Rt△ACD中,AD===2,∴tan∠OBC=tan∠CAD===.
第1题解图
同课章节目录
