《第3章整式及其加减》同步达标测试题 2022-2023学年鲁教版(五四制)六年级数学上册(含答案)
文档属性
| 名称 | 《第3章整式及其加减》同步达标测试题 2022-2023学年鲁教版(五四制)六年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 104.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 13:42:27 | ||
图片预览



文档简介
2022-2023学年鲁教版六年级数学上册《第3章整式及其加减》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.“m与n差的3倍”用代数式可以表示成( )
A.3m﹣n B.m﹣3n C.3(n﹣m) D.3(m﹣n)
2.若﹣2xm+7y4与3x4y2n是同类项,则mn的值为( )
A.1 B.5 C.6 D.﹣6
3.某种苹果的售价是m元/kg(m<20),现用100元买5kg这种苹果,应找回( )
A.5m元 B.(100﹣5m)元 C.(5m﹣100)元 D.(5m+100)元
4.按一定规律排列的单项式:a,﹣3a2,5a3,﹣7a4,9a5,﹣11a6,…,第2022个单项式是( )
A.4043a2022 B.﹣4043a2022 C.4045a2022 D.﹣4045a2022
5.下列算式中正确的是( )
A.4x﹣3x=1 B.2x+3y=3xy
C.3x2+2x3=5x5 D.x2﹣3x2=﹣2x2
6.已知a为任意实数,有多项式M=2x2+3ax+5,N=x+4,且MN=A,当多项式A中不含2次项时,a的值为( )
A.﹣ B.﹣1 C.0 D.1
7.若代数式2(x+1)+3(x+2)的值为8,则代数式2(x﹣2)+3(x﹣1)的值为( )
A.0 B.11 C.﹣7 D.﹣15
8.按如图所示的运算程序,能使输出y值为3的是( )
A.x=1 B.x=2 C.x=3 D.x=4
二.填空题(共8小题,满分40分)
9.已知﹣xm+3y与2x4yn+3是同类项,则(m+n)2021的值是 .
10.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.
(1)现购进a本甲种书和b本乙种书.请用含a,b的代数式表示,共付款( )元;
(2)若花费5×104元购进甲种书、花费3×103元购进乙种书,
用科学记数法表示共花费 元.
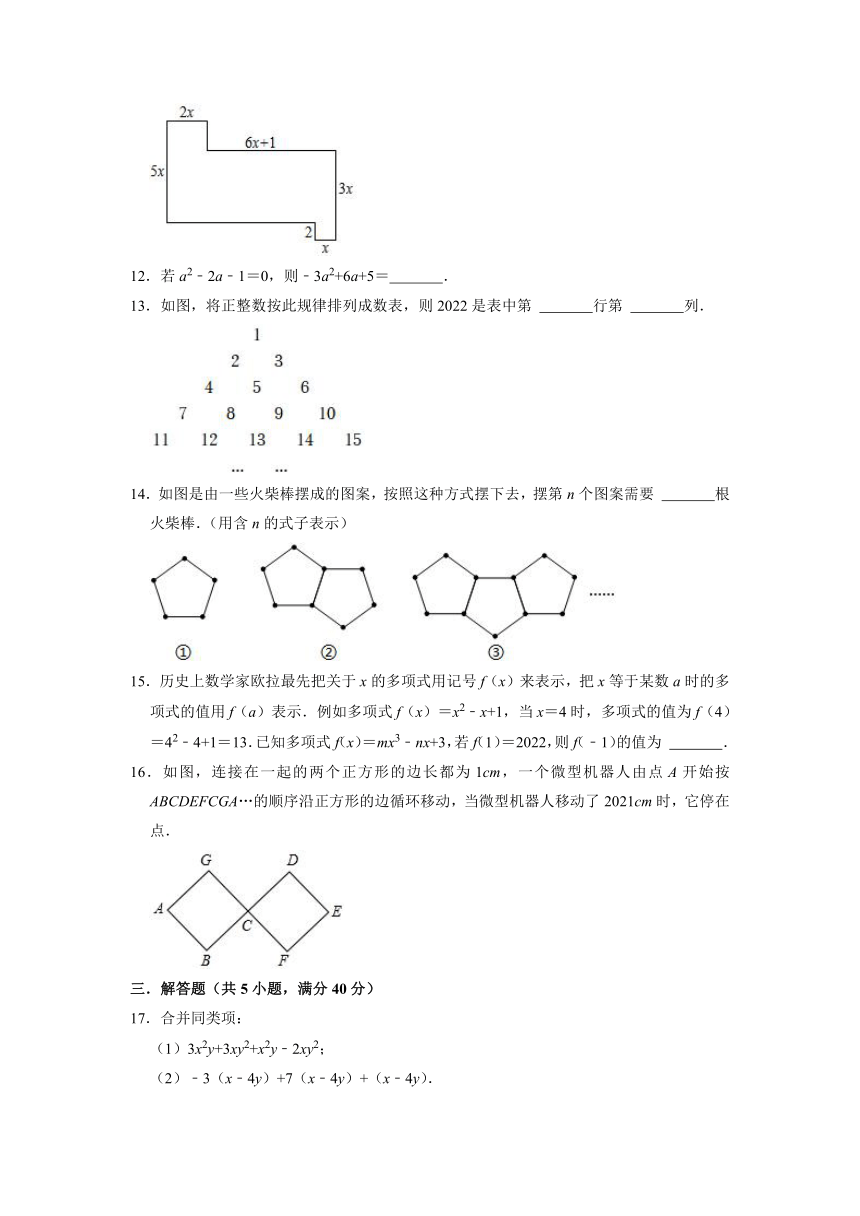
11.如图所示是小明设计的一个图案,则该图案的面积用含x的代数式表示为 .
12.若a2﹣2a﹣1=0,则﹣3a2+6a+5= .
13.如图,将正整数按此规律排列成数表,则2022是表中第 行第 列.
14.如图是由一些火柴棒摆成的图案,按照这种方式摆下去,摆第n个图案需要 根火柴棒.(用含n的式子表示)
15.历史上数学家欧拉最先把关于x的多项式用记号f(x)来表示,把x等于某数a时的多项式的值用f(a)表示.例如多项式f(x)=x2﹣x+1,当x=4时,多项式的值为f(4)=42﹣4+1=13.已知多项式f(x)=mx3﹣nx+3,若f(1)=2022,则f(﹣1)的值为 .
16.如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动,当微型机器人移动了2021cm时,它停在 点.
三.解答题(共5小题,满分40分)
17.合并同类项:
(1)3x2y+3xy2+x2y﹣2xy2;
(2)﹣3(x﹣4y)+7(x﹣4y)+(x﹣4y).
18.先化简,再求值:﹣3(a2﹣b)+5(3b+a2),其中a=﹣2,b=﹣1.
19.临近春节,小明去超市买了若干盏灯笼和若干副春联,准备送给贫困户,已知每盏灯笼的价格为25元,每副春联的价格为20元.现买了a盏灯笼和b副春联,共花费y元.
(1)用含a,b的代数式表示y.
(2)如果a=10,y=470,则b的值为多少?
20.先化简,再求值:
已知:A=x2﹣3xy+y2,B=4x2﹣13xy+4y2,求5A﹣(﹣6A+4B)的值,其中x,y满足(y﹣1)2+|x+3|=0.
21.请观察下列算式:
(1),,,.
则第10个算式为 = .
第n个算式为 = .
(2)运用以上规律计算:= .
(3)仿照以上方法计算:.
参考答案
一.选择题(共8小题,满分40分)
1.解:“m与n差的3倍”用代数式可以表示为:3(m﹣n).
故选:D.
2.解:由同类项的概念可知:m+7=4,2n=4,
解得:m=﹣3,n=2,
∴mn=(﹣3)×2=﹣6,
故选:D.
3.解:由题意得:应找回:(100﹣5m)元,
故选:B.
4.解:∵一列单项式:a,﹣3a2,5a3,﹣7a4,9a5,﹣11a6,…,
∴第n个单项式为(﹣1)n+1 (2n﹣1) an,
∴第2022个单项式为:(﹣1)2022+1 (2×2022﹣1) a2022=﹣4043a2022.
故选:B.
5.解:A、原式=x,故A不符合题意.
B、2x与3y不是同类项,不能合并,故B不符合题意.
C、3x2与2x3不是同类项,不能合并,故C不符合题意.
D、x2﹣3x2=﹣2x2,故D符合题意.
故选:D.
6.解:A=MN=(2x2+3ax+5)(x+4)=2x3+8x2+3ax2+12ax+5x+20=2x3+(3a+8)x2+(12a+5)x+20,
∵多项式A中不含2次项,
∴3a+8=0,
∴a=﹣.
故选:A.
7.解:∵2(x+1)+3(x+2)=8
∴2x+2+3x+6=8
5x=0
x=0,
把x=0代入原式=2×(﹣2)﹣3=﹣7,
故选:C.
8.解:当x=1时,1是奇数,y==6;
当x=2时,2是偶数,y=+1=2;
当x=3时,3是奇数,y==2;
当x=4时,4是偶数,y=+1=3;
∴按如图所示的运算程序,能使输出y值为3的是x=4.
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵﹣xm+3y与2x4yn+3是同类项,
∴m+3=4,n+3=1,
解得m=1,n=﹣2,
∴(m+n)2021=(1﹣2)2021=﹣1,
故答案为:﹣1.
10.解:(1)购买两种书的总价为:(4a+10b)元,
故答案为:4a+10b;
(2)5×104+3×103
=50×103+3×103
=53×103
=5.3×104,
故答案为:5.3×104.
11.解:如图,
该图案的面积为:2x [5x﹣(3x﹣2)]+(2x+6x+1)(3x﹣2)+2x
=2x(2x+2)+(8x+1)(3x﹣2)+2x
=4x2+4x+24x2﹣16x+3x﹣2+2x
=28x2﹣7x﹣2,
故答案为:28x2﹣7x﹣2.
12.解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴原式=﹣3(a2﹣2a)+5
=﹣3×1+5
=﹣3+5
=2.
故答案为:2.
13.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2022<,2022﹣=2022﹣2016=6,
∴2022是表中第64行第6列,
故答案为:64,6.
14.解:观察图形的变化可知:
摆第1个图案要用火柴棒的根数为:5;
摆第2个图案要用火柴棒的根数为:9=5+4=5+4×1;
摆第3个图案要用火柴棒的根数为:13=5+4+4=5+4×2;
...
则摆第n个图案要用火柴棒的根数为:5+4(n﹣1)=4n+1.
故答案为:(4n+1).
15.解:当x=1时,
f(1)=m×13﹣n×(1)+3=m﹣n+3,
∵f(1)=2022,
∴m﹣n+3=2022,
∴m﹣n=2019,
∴f(﹣1)=m×(﹣1)3﹣n×(﹣1)+3
=﹣(m﹣n)+3
=﹣2019+3
=﹣2016.
故答案为:﹣2016.
16.解:∵两个正方形的边长都为1cm,
∴从A开始移动8cm后回到点A,
∵2021÷8=252…5,
∴移动2021cm时停在点F处.
故答案为:F.
三.解答题(共5小题,满分40分)
17.解:(1)3x2y+3xy2+x2y﹣2xy2
=(3x2y+x2y)+(3xy2﹣2xy2)
=4x2y+xy2;
(2)﹣3(x﹣4y)+7(x﹣4y)+(x﹣4y)
=(﹣3+7+1)(x﹣4y)
=5(x﹣4y)
=5x﹣20y.
18.解:原式=﹣3a2+3b+15b+5a2
=2a2+18b,
当a=﹣2,b=﹣1时,
原式=2×(﹣2)2+18×(﹣1)
=8﹣18
=﹣10.
19.解:(1)每盏灯笼的价格为25元,买a盏,则用了25a元;每副春联的价格为20元,买b副,则用了20b元.
∴y=25a+20b.
故答案为:y=25a+20b.
(2)由(1)知y=25a+20b.
当a=10,y=470时,
得10×25+20b=470,
解得:b=11.
故答案为:b=11.
20.解:∵(y﹣1)2+|x+3|=0,(y﹣1)2≥0,|x+3|≥0,
∴y﹣1=0,x+3=0,
∴x=﹣3,y=1.
原式=5A+3A﹣2B
=8A﹣2B
=8(x2﹣3xy+y2)﹣2(4x2﹣13xy+4y2)
=8x2﹣24xy+8y2﹣8x2+26xy﹣8y2
=2xy;
当x=﹣3,y=1时,
原式=2×(﹣3)×1
=﹣6.
21.解:(1)∵,,,,
∴第n个算式为:=,
则第10个算式为:=,
故答案为:,,,;
(2)
=+++...+++
=1﹣+﹣++...+++
=1﹣
=,
故答案为:;
(3)
=+++...++
=×(1﹣+++...++)
=×(1﹣)
=×
=
一.选择题(共8小题,满分40分)
1.“m与n差的3倍”用代数式可以表示成( )
A.3m﹣n B.m﹣3n C.3(n﹣m) D.3(m﹣n)
2.若﹣2xm+7y4与3x4y2n是同类项,则mn的值为( )
A.1 B.5 C.6 D.﹣6
3.某种苹果的售价是m元/kg(m<20),现用100元买5kg这种苹果,应找回( )
A.5m元 B.(100﹣5m)元 C.(5m﹣100)元 D.(5m+100)元
4.按一定规律排列的单项式:a,﹣3a2,5a3,﹣7a4,9a5,﹣11a6,…,第2022个单项式是( )
A.4043a2022 B.﹣4043a2022 C.4045a2022 D.﹣4045a2022
5.下列算式中正确的是( )
A.4x﹣3x=1 B.2x+3y=3xy
C.3x2+2x3=5x5 D.x2﹣3x2=﹣2x2
6.已知a为任意实数,有多项式M=2x2+3ax+5,N=x+4,且MN=A,当多项式A中不含2次项时,a的值为( )
A.﹣ B.﹣1 C.0 D.1
7.若代数式2(x+1)+3(x+2)的值为8,则代数式2(x﹣2)+3(x﹣1)的值为( )
A.0 B.11 C.﹣7 D.﹣15
8.按如图所示的运算程序,能使输出y值为3的是( )
A.x=1 B.x=2 C.x=3 D.x=4
二.填空题(共8小题,满分40分)
9.已知﹣xm+3y与2x4yn+3是同类项,则(m+n)2021的值是 .
10.某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.
(1)现购进a本甲种书和b本乙种书.请用含a,b的代数式表示,共付款( )元;
(2)若花费5×104元购进甲种书、花费3×103元购进乙种书,
用科学记数法表示共花费 元.
11.如图所示是小明设计的一个图案,则该图案的面积用含x的代数式表示为 .
12.若a2﹣2a﹣1=0,则﹣3a2+6a+5= .
13.如图,将正整数按此规律排列成数表,则2022是表中第 行第 列.
14.如图是由一些火柴棒摆成的图案,按照这种方式摆下去,摆第n个图案需要 根火柴棒.(用含n的式子表示)
15.历史上数学家欧拉最先把关于x的多项式用记号f(x)来表示,把x等于某数a时的多项式的值用f(a)表示.例如多项式f(x)=x2﹣x+1,当x=4时,多项式的值为f(4)=42﹣4+1=13.已知多项式f(x)=mx3﹣nx+3,若f(1)=2022,则f(﹣1)的值为 .
16.如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动,当微型机器人移动了2021cm时,它停在 点.
三.解答题(共5小题,满分40分)
17.合并同类项:
(1)3x2y+3xy2+x2y﹣2xy2;
(2)﹣3(x﹣4y)+7(x﹣4y)+(x﹣4y).
18.先化简,再求值:﹣3(a2﹣b)+5(3b+a2),其中a=﹣2,b=﹣1.
19.临近春节,小明去超市买了若干盏灯笼和若干副春联,准备送给贫困户,已知每盏灯笼的价格为25元,每副春联的价格为20元.现买了a盏灯笼和b副春联,共花费y元.
(1)用含a,b的代数式表示y.
(2)如果a=10,y=470,则b的值为多少?
20.先化简,再求值:
已知:A=x2﹣3xy+y2,B=4x2﹣13xy+4y2,求5A﹣(﹣6A+4B)的值,其中x,y满足(y﹣1)2+|x+3|=0.
21.请观察下列算式:
(1),,,.
则第10个算式为 = .
第n个算式为 = .
(2)运用以上规律计算:= .
(3)仿照以上方法计算:.
参考答案
一.选择题(共8小题,满分40分)
1.解:“m与n差的3倍”用代数式可以表示为:3(m﹣n).
故选:D.
2.解:由同类项的概念可知:m+7=4,2n=4,
解得:m=﹣3,n=2,
∴mn=(﹣3)×2=﹣6,
故选:D.
3.解:由题意得:应找回:(100﹣5m)元,
故选:B.
4.解:∵一列单项式:a,﹣3a2,5a3,﹣7a4,9a5,﹣11a6,…,
∴第n个单项式为(﹣1)n+1 (2n﹣1) an,
∴第2022个单项式为:(﹣1)2022+1 (2×2022﹣1) a2022=﹣4043a2022.
故选:B.
5.解:A、原式=x,故A不符合题意.
B、2x与3y不是同类项,不能合并,故B不符合题意.
C、3x2与2x3不是同类项,不能合并,故C不符合题意.
D、x2﹣3x2=﹣2x2,故D符合题意.
故选:D.
6.解:A=MN=(2x2+3ax+5)(x+4)=2x3+8x2+3ax2+12ax+5x+20=2x3+(3a+8)x2+(12a+5)x+20,
∵多项式A中不含2次项,
∴3a+8=0,
∴a=﹣.
故选:A.
7.解:∵2(x+1)+3(x+2)=8
∴2x+2+3x+6=8
5x=0
x=0,
把x=0代入原式=2×(﹣2)﹣3=﹣7,
故选:C.
8.解:当x=1时,1是奇数,y==6;
当x=2时,2是偶数,y=+1=2;
当x=3时,3是奇数,y==2;
当x=4时,4是偶数,y=+1=3;
∴按如图所示的运算程序,能使输出y值为3的是x=4.
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵﹣xm+3y与2x4yn+3是同类项,
∴m+3=4,n+3=1,
解得m=1,n=﹣2,
∴(m+n)2021=(1﹣2)2021=﹣1,
故答案为:﹣1.
10.解:(1)购买两种书的总价为:(4a+10b)元,
故答案为:4a+10b;
(2)5×104+3×103
=50×103+3×103
=53×103
=5.3×104,
故答案为:5.3×104.
11.解:如图,
该图案的面积为:2x [5x﹣(3x﹣2)]+(2x+6x+1)(3x﹣2)+2x
=2x(2x+2)+(8x+1)(3x﹣2)+2x
=4x2+4x+24x2﹣16x+3x﹣2+2x
=28x2﹣7x﹣2,
故答案为:28x2﹣7x﹣2.
12.解:∵a2﹣2a﹣1=0,
∴a2﹣2a=1,
∴原式=﹣3(a2﹣2a)+5
=﹣3×1+5
=﹣3+5
=2.
故答案为:2.
13.解:由图可知,
第一行1个数字,
第二行2个数字,
第三行3个数字,
…,
则第n行n个数字,
前n行一共有个数字,
∵<2022<,2022﹣=2022﹣2016=6,
∴2022是表中第64行第6列,
故答案为:64,6.
14.解:观察图形的变化可知:
摆第1个图案要用火柴棒的根数为:5;
摆第2个图案要用火柴棒的根数为:9=5+4=5+4×1;
摆第3个图案要用火柴棒的根数为:13=5+4+4=5+4×2;
...
则摆第n个图案要用火柴棒的根数为:5+4(n﹣1)=4n+1.
故答案为:(4n+1).
15.解:当x=1时,
f(1)=m×13﹣n×(1)+3=m﹣n+3,
∵f(1)=2022,
∴m﹣n+3=2022,
∴m﹣n=2019,
∴f(﹣1)=m×(﹣1)3﹣n×(﹣1)+3
=﹣(m﹣n)+3
=﹣2019+3
=﹣2016.
故答案为:﹣2016.
16.解:∵两个正方形的边长都为1cm,
∴从A开始移动8cm后回到点A,
∵2021÷8=252…5,
∴移动2021cm时停在点F处.
故答案为:F.
三.解答题(共5小题,满分40分)
17.解:(1)3x2y+3xy2+x2y﹣2xy2
=(3x2y+x2y)+(3xy2﹣2xy2)
=4x2y+xy2;
(2)﹣3(x﹣4y)+7(x﹣4y)+(x﹣4y)
=(﹣3+7+1)(x﹣4y)
=5(x﹣4y)
=5x﹣20y.
18.解:原式=﹣3a2+3b+15b+5a2
=2a2+18b,
当a=﹣2,b=﹣1时,
原式=2×(﹣2)2+18×(﹣1)
=8﹣18
=﹣10.
19.解:(1)每盏灯笼的价格为25元,买a盏,则用了25a元;每副春联的价格为20元,买b副,则用了20b元.
∴y=25a+20b.
故答案为:y=25a+20b.
(2)由(1)知y=25a+20b.
当a=10,y=470时,
得10×25+20b=470,
解得:b=11.
故答案为:b=11.
20.解:∵(y﹣1)2+|x+3|=0,(y﹣1)2≥0,|x+3|≥0,
∴y﹣1=0,x+3=0,
∴x=﹣3,y=1.
原式=5A+3A﹣2B
=8A﹣2B
=8(x2﹣3xy+y2)﹣2(4x2﹣13xy+4y2)
=8x2﹣24xy+8y2﹣8x2+26xy﹣8y2
=2xy;
当x=﹣3,y=1时,
原式=2×(﹣3)×1
=﹣6.
21.解:(1)∵,,,,
∴第n个算式为:=,
则第10个算式为:=,
故答案为:,,,;
(2)
=+++...+++
=1﹣+﹣++...+++
=1﹣
=,
故答案为:;
(3)
=+++...++
=×(1﹣+++...++)
=×(1﹣)
=×
=
