人教版五上 数学 第三单元《小数除法》教材解读(共22张PPT)
文档属性
| 名称 | 人教版五上 数学 第三单元《小数除法》教材解读(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
《小数除法》教材解读
新人教版数学五年级上册第三单元
数与代数
统计与概率
图形与几何
综合与实践
目录
1
单元教材分析
2
课标解读及核心素养
3
单元教学目标及重难点
4
教材例题解析
5
教学实施建议
单元教材分析
本单元主要学习的内容有:除数是整数的小数除法—个数除以小数、商的近似数、循环小数、用计算器探索规律、解决问题以及整理和复习。教材在编排时通过晨练、编制中国结、买羽毛球等与现实生活息息相关的情境引出有关小数除法的一系列间题。小数除法的计算法则、试商的方法都与整数除法有关,因此教材重点突出怎样把除数是小数的除法转化成除数是整数的除法,多处以加强提示的方式向学生展示探究的过程。商的近似值和循环小数都是进一步研究商,通过学习,学生可以根据具体情况灵活地处理商,并认识循环小数等有关概念。而用计算器探索规律,既可使学生学习借助计算工具探索数学规律,又可激发学生的学习兴趣。
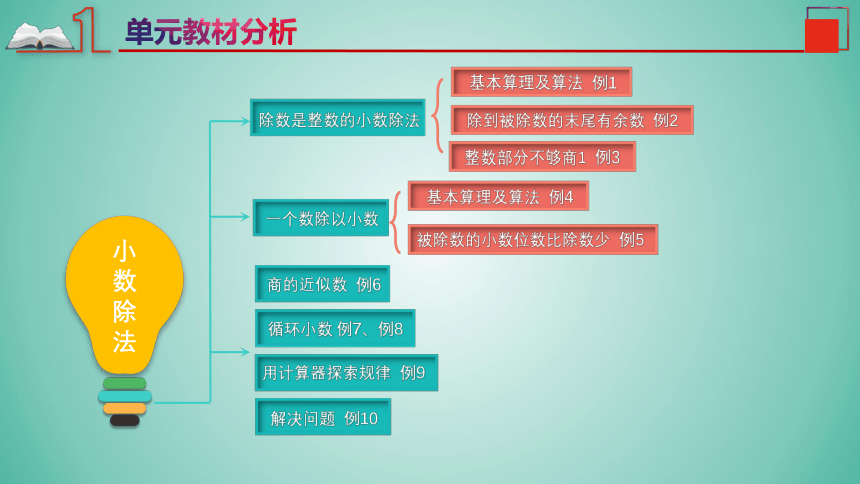
除数是整数的小数除法
小
数
除
法
基本算理及算法 例1
除到被除数的末尾有余数 例2
整数部分不够商1 例3
被除数的小数位数比除数少 例5
单元教材分析
一个数除以小数
基本算理及算法 例4
商的近似数 例6
循环小数 例7、例8
用计算器探索规律 例9
解决问题 例10
教材编排特点
01
02
03
结合具体情境,充分利用学生的生活经验和已有知识,引导学生自主探索小数除法的计算方法。
重视计算方法的概括,给出计算法则的结语。
练习、例题的设计既有巩固,又有铺垫。
单元教材分析
课标解读及核心素养
课
标
解
读
《义务教育数学课程标准(2022年版)》在“学段目标”的“第二学段”中提出:“理解分数、小数、百分数的意义,了解负数的意义;掌握必要的运算技能;理解估算的意义”“能借助计算器解决简单的应用问题”“在观察、实验、猜想、验证等活动中,发展合情推理能力,能进行有条理的思考,能比较清楚地表达自己的思考过程与结果”“尝试从日常生活中发现并提出简单的数学问题,并运用一些知识加以解决”“能探索分析和解决简单问题的有效方法,了解解决问题方法的多样性”“能回顾解决问题的过程,初步判断结果的合理性”。
数学
抽象
数学
建模
数据
分析
直观
想象
逻辑
推理
数学
运算
会用数学的眼光观察世界
会用数学的思维思考世界
会用数学的语言表达世界
课标解读及核心素养
2
4
1
3
使学生掌握小数除法的计算方法,能正确地进行计算;能根据算式特点,合理选择口算、笔算、估算、简算等方法灵活计算。
使学生掌握用“四舍五入”法截取商是小数的近似值,能根据实际情况合理运用“进一法”和“去尾法” 截取商的近似值。
使学生初步认识循环小数、有限小数和无限小数;使学生能借助计算器探索规律,并应用规律解决问题。能应用小数除法及其他运算解决一些实际问题。
在小数除法简单实际问题解决的过程中,使学生体会小数除法的应用价值。
单元教学目标及重难点
单元教学目标及重难点
教学难点
教学重点
体会除法运算的意义,在理解的基础上掌握2~6的乘法口诀求商的方法及用除法解决问题。
除法是小数的小数除法商的小数点位置的确定。
教学重点
小数除法的计算原理。
教材例题解析
解决“每周应跑多少千米”时,着重以下四个环节:
①根据数量关系列出除法算式。②计算前先估计计算结果。
③让学生用已有知识探索“22.4:4”的计算方法。
④让学生用已有的知识经验解释竖式计算过程,理解商的小数点为什么要和被除数的小数点对齐。
除数是整数的小数除法安排了3个例题。例1和例2是两种基本情况,例3是特殊情况。例1是除到被除数的末尾没有余数,能除尽的情形。
根据除法的意义引出小数除以整数的算式,计算时教材呈现了两种方法。一种是将千米数转化为米数,把小数除以整数的除法转化成整数除法。另一种是根据小数意义,理解用竖式计算的方法。这种方法是学习的重点,核心是帮助学生理解为什么商的小数,点要和被除数的小数点对齐。
联系数的意义进行算理指导,利用情境支撑算理理解,促进小数除法计算方法的形成。
关注算理算法的沟通与联系教学时,需要梳理整数除法与小数除法的共同点与不同点,让学生明确整数除法和小数除法的计算。
教材例题解析
例2是除到被除数的末尾仍有余数,需要添0继续除。结合小数意义说明“为什么添0继续除后,商要写在十分位上”
通过想一想提示引导学生总结小数除以整数的计算方法以及要注意的地方。
例3是被除数比除数小,整数部分不够商1的特殊情况。结合意义说明“为什么要在商的个位商0”的算理。
教材还提出“验算”的要求。一方面加深乘、除法之间关系的理解;另一方面强化验算的意识和习惯。虽然安排在例3之后,并不意味着只有此题才需要验算,而应将习惯培养贯穿于小数除法学习的始终。
将估算融于其中,加强对结果合理性的反思
引导自主探索、自主概括总结计算方法
教材例题解析
例4是被除数和除数的小数位数相同,用编“中国结”的情境引入,借助“一共的米数÷每个结的米数=个数”列出算式,引出所学内容。
在计算方法的探讨上,教材用“想一想,除数是小数怎么计算?”突出讨论重,点后,用小男孩的话说明解决这个问题的基本方法是“把除数转化成整数”。
教材呈现了根据商不变的性质,把除数和被除数同时扩大到原来的100倍,使除数变成整数的过程。最后给出竖式的简便写法,即画去除数的小数点和前面的0,以及被除数的小数点,说明除数和被除数都扩大到原来的100倍,小数点都向右移动了两位。
转化思想
鼓励探究算法,体会“转化”思想教学时可以让学生经历这几个过程:根据情境的数量关系列出算式;估计编“中国结”的个数;利用已有经验和知识探索计算方法,可能会有两种方法,即转化成“厘米数”计算和利用商不变的性质转化;交流算法,体会两种方法之间的联系与共同点,都是“将除数转化为整数”;讨论竖式表达的规范性和简洁性。
教材例题解析
例5教学被除数的小数位数比除数的小数位数少的情况。通过提问“被除数的位数不够怎么办?”,引起学生思考。并通过虚线框里的图示,说明把除数变成整数,小数点要向右移动两位,根据商不变的性质,被除数也要右移两位,而它只有一位小数,所以要在它的末尾用“0”补足。
教材用讨论来引导学生总结小数除法的计算方法。提示教师:计算方法的得出应基于学生的自主反思、充分交流,在学生概括的基础上加以提炼与完善。
应用迁移
探究方法
重视算法
整理提炼
一看:看清除数有几位小数;
二移:把除数和被除数的小数点同时向右移动相同的位数,使除数变成整数。当被除数位数不足时,用“0”补足;
三算:按照除数是整数的小数除法的方法计算。
教材例题解析
例6教学求商的近似数。一是体会求商的近似数的必要性;二是掌握取商的近似值的方法。
教材提供“求每个羽毛球的价钱”的情境,让学生感受取商的近似值是实际应用的需要。教材首先让学生理解在解决实际问题时,遇到除不尽的情况,可以取商的近似值。
其次,让学生明白可以根据需要取不同精确度的近似值。如,计算价钱可以精确到“分”,即保留两位小数;也可以精确到“角”,即保留一位小数。
适当补充问题,突出取近似值的意义。小数除法中取近似值有两种情况,一是除不尽的时候;一是除得尽,但是小数位数比较多,根据实际情况不用这么多。例题是在除不尽时的情况下,根据实际需要取近似值。
教材例题解析
例7是教学商从某一位起,一个数字重复出现的情况,为认识循环小数提供感性材料。
教材创设了王鹏赛跑的情境,通过解决问题,引出400÷75。让学生通过实际计算,发现这道题无论除到小数点后面多少位,都除不尽。由此让学生观察这个竖式,看有什么发现。学生会发现余数“25”重复不断出现,商“3”也重复不断出现。
例8通过计算两道除法式题,呈现了除不尽时商的两种情况:一种是从某位起重复出现某一个数字;另一种是从某位起几个数字依次不断重复出现。由此引出循环小数的概念。
引导探究商循环出现的原因
重观察、比较、概括
这里要注意两点:一是结果用“=”;二是适时将算式过程优化。除的过程中,只要余数第二次重复出现,就不必再除,可以确定商。
教材例题解析
在教学“循环小数”概念之后,教材介绍了循环节的概念,给出循环小数的简便记法。
值得注意的是,如果用循环小数表示用“=”连接,如果用近似数表示则用“≈”连接。
教材结合具体算式用“算一算、想一想”的方式组织学生讨论“两个数相除,如果不能得到整数商,所得的商会有哪些情况”,得出两个数相除时商的两种情况,一种是能除尽的情况,商是有限小数;一种是除不尽的情况,商是无限循环小数。在此基础上,介绍有限小数和无限小数的概念。
厘清概念之间的联系。教学有限小数和无限小数的概念时,可以结合大量的实例让学生讨论后明确,如果不能得到整数的商,会有两种情况。由此引出有限小数和无限小数的概念,并说明我们现在学习的小数范围比以前又扩大了,又增加了无限小数,而循环小数就是一种无限小数。但要注意,无限小数除了循环小数外,还有无限不循环小数
教材例题解析
例9教学用计算器探索规律。有三方面的作用:一是巩固循环小数;二是熟练计算器的使用;三是探索规律,但教学重心是规律的探索。
用计算器计算
观察发现规律
利用规律写商
做一做:引导学生观察算式有怎样的规律,可以培养观察的能力。从上往下观察被乘数、乘数是怎样变化的,积是怎样变化的。帮助学生形成观察的方法,分析算式之间的关系。接下来,学生概括表达规律,接写下一个算式,得出一个一般的规律,并进行类推。
教材例题解析
例10是根据实际需要用“进一法”和“去尾法”取商的近似值。
体会根据实际情况用“去尾法”“进一法”取近似值的必要性。由于这两道题算出的结果都是小数,而需要准备的瓶子和包装的礼品盒都必须是整数,因此都要取这些计算结果的近似值。
取近似值时,不能机械地使用“四舍五入”法,要根据具体情况确定“舍”还是“入”。
进一法
去尾法
利用已有经验尝试解决问题,交流体会优化方法
学生可能会有以下几种解法
①0.4×6=2.4(千克)6+1=7(个);
②2.5÷0.4≈6(个)6+1=7(个):③2.5÷0.4=6.25(个)6+1=7(个)
教学实施建议
抓住新旧知识的连接点,在理解算理的基础上,引导学生通过讨论总结小数除法的计算方法。
本单元内容与旧知识联系十分紧密。小数除法的计算法则是以整数除法中被除数和除数同时乘上相同的数(0除外)商不变,以及小数点位置移动规律等知识为基础来说明的。小数除法的试商方法、除的步骤和整数除法基本相同,不同的只是小数点的处理问题。因此,要注意复习和运用整数除法的有关知识,为新知识的学习奠定好基础。
同小数乘法一样,教学中要让学生在理解算理的基础上,及时归纳、总结小数除法的计算方法,帮助学生形成良好的计算能力。
教学实施建议
要注意突出重点,攻破难点。
除数是整数的小数除法,要注意讲明商的小数点为什么与被除数的小数点对齐。小数除以小数,要重点说明除数怎样转化为整数。讲清了一般的计算原理,注意克服难点:小数点的处理问题。学生在计算中经常出现只去掉除数的小数点,而不把被除数的小数点相应地向右移动,或者把小数点的位置移错,使商的小数点常常处理错。为了帮助学生攻破难点,可适当安排有针对性的单项练习。教学中,一方面需要关注要点,重视“除数位数与被除数的小数位数不同”这一除法类型;另一方面,需要加强商中间有0的除法的铺垫与练习,以弥补薄弱,突破难点。
谢谢欣赏
THANK YOU FOR LISTENING
《小数除法》教材解读
新人教版数学五年级上册第三单元
数与代数
统计与概率
图形与几何
综合与实践
目录
1
单元教材分析
2
课标解读及核心素养
3
单元教学目标及重难点
4
教材例题解析
5
教学实施建议
单元教材分析
本单元主要学习的内容有:除数是整数的小数除法—个数除以小数、商的近似数、循环小数、用计算器探索规律、解决问题以及整理和复习。教材在编排时通过晨练、编制中国结、买羽毛球等与现实生活息息相关的情境引出有关小数除法的一系列间题。小数除法的计算法则、试商的方法都与整数除法有关,因此教材重点突出怎样把除数是小数的除法转化成除数是整数的除法,多处以加强提示的方式向学生展示探究的过程。商的近似值和循环小数都是进一步研究商,通过学习,学生可以根据具体情况灵活地处理商,并认识循环小数等有关概念。而用计算器探索规律,既可使学生学习借助计算工具探索数学规律,又可激发学生的学习兴趣。
除数是整数的小数除法
小
数
除
法
基本算理及算法 例1
除到被除数的末尾有余数 例2
整数部分不够商1 例3
被除数的小数位数比除数少 例5
单元教材分析
一个数除以小数
基本算理及算法 例4
商的近似数 例6
循环小数 例7、例8
用计算器探索规律 例9
解决问题 例10
教材编排特点
01
02
03
结合具体情境,充分利用学生的生活经验和已有知识,引导学生自主探索小数除法的计算方法。
重视计算方法的概括,给出计算法则的结语。
练习、例题的设计既有巩固,又有铺垫。
单元教材分析
课标解读及核心素养
课
标
解
读
《义务教育数学课程标准(2022年版)》在“学段目标”的“第二学段”中提出:“理解分数、小数、百分数的意义,了解负数的意义;掌握必要的运算技能;理解估算的意义”“能借助计算器解决简单的应用问题”“在观察、实验、猜想、验证等活动中,发展合情推理能力,能进行有条理的思考,能比较清楚地表达自己的思考过程与结果”“尝试从日常生活中发现并提出简单的数学问题,并运用一些知识加以解决”“能探索分析和解决简单问题的有效方法,了解解决问题方法的多样性”“能回顾解决问题的过程,初步判断结果的合理性”。
数学
抽象
数学
建模
数据
分析
直观
想象
逻辑
推理
数学
运算
会用数学的眼光观察世界
会用数学的思维思考世界
会用数学的语言表达世界
课标解读及核心素养
2
4
1
3
使学生掌握小数除法的计算方法,能正确地进行计算;能根据算式特点,合理选择口算、笔算、估算、简算等方法灵活计算。
使学生掌握用“四舍五入”法截取商是小数的近似值,能根据实际情况合理运用“进一法”和“去尾法” 截取商的近似值。
使学生初步认识循环小数、有限小数和无限小数;使学生能借助计算器探索规律,并应用规律解决问题。能应用小数除法及其他运算解决一些实际问题。
在小数除法简单实际问题解决的过程中,使学生体会小数除法的应用价值。
单元教学目标及重难点
单元教学目标及重难点
教学难点
教学重点
体会除法运算的意义,在理解的基础上掌握2~6的乘法口诀求商的方法及用除法解决问题。
除法是小数的小数除法商的小数点位置的确定。
教学重点
小数除法的计算原理。
教材例题解析
解决“每周应跑多少千米”时,着重以下四个环节:
①根据数量关系列出除法算式。②计算前先估计计算结果。
③让学生用已有知识探索“22.4:4”的计算方法。
④让学生用已有的知识经验解释竖式计算过程,理解商的小数点为什么要和被除数的小数点对齐。
除数是整数的小数除法安排了3个例题。例1和例2是两种基本情况,例3是特殊情况。例1是除到被除数的末尾没有余数,能除尽的情形。
根据除法的意义引出小数除以整数的算式,计算时教材呈现了两种方法。一种是将千米数转化为米数,把小数除以整数的除法转化成整数除法。另一种是根据小数意义,理解用竖式计算的方法。这种方法是学习的重点,核心是帮助学生理解为什么商的小数,点要和被除数的小数点对齐。
联系数的意义进行算理指导,利用情境支撑算理理解,促进小数除法计算方法的形成。
关注算理算法的沟通与联系教学时,需要梳理整数除法与小数除法的共同点与不同点,让学生明确整数除法和小数除法的计算。
教材例题解析
例2是除到被除数的末尾仍有余数,需要添0继续除。结合小数意义说明“为什么添0继续除后,商要写在十分位上”
通过想一想提示引导学生总结小数除以整数的计算方法以及要注意的地方。
例3是被除数比除数小,整数部分不够商1的特殊情况。结合意义说明“为什么要在商的个位商0”的算理。
教材还提出“验算”的要求。一方面加深乘、除法之间关系的理解;另一方面强化验算的意识和习惯。虽然安排在例3之后,并不意味着只有此题才需要验算,而应将习惯培养贯穿于小数除法学习的始终。
将估算融于其中,加强对结果合理性的反思
引导自主探索、自主概括总结计算方法
教材例题解析
例4是被除数和除数的小数位数相同,用编“中国结”的情境引入,借助“一共的米数÷每个结的米数=个数”列出算式,引出所学内容。
在计算方法的探讨上,教材用“想一想,除数是小数怎么计算?”突出讨论重,点后,用小男孩的话说明解决这个问题的基本方法是“把除数转化成整数”。
教材呈现了根据商不变的性质,把除数和被除数同时扩大到原来的100倍,使除数变成整数的过程。最后给出竖式的简便写法,即画去除数的小数点和前面的0,以及被除数的小数点,说明除数和被除数都扩大到原来的100倍,小数点都向右移动了两位。
转化思想
鼓励探究算法,体会“转化”思想教学时可以让学生经历这几个过程:根据情境的数量关系列出算式;估计编“中国结”的个数;利用已有经验和知识探索计算方法,可能会有两种方法,即转化成“厘米数”计算和利用商不变的性质转化;交流算法,体会两种方法之间的联系与共同点,都是“将除数转化为整数”;讨论竖式表达的规范性和简洁性。
教材例题解析
例5教学被除数的小数位数比除数的小数位数少的情况。通过提问“被除数的位数不够怎么办?”,引起学生思考。并通过虚线框里的图示,说明把除数变成整数,小数点要向右移动两位,根据商不变的性质,被除数也要右移两位,而它只有一位小数,所以要在它的末尾用“0”补足。
教材用讨论来引导学生总结小数除法的计算方法。提示教师:计算方法的得出应基于学生的自主反思、充分交流,在学生概括的基础上加以提炼与完善。
应用迁移
探究方法
重视算法
整理提炼
一看:看清除数有几位小数;
二移:把除数和被除数的小数点同时向右移动相同的位数,使除数变成整数。当被除数位数不足时,用“0”补足;
三算:按照除数是整数的小数除法的方法计算。
教材例题解析
例6教学求商的近似数。一是体会求商的近似数的必要性;二是掌握取商的近似值的方法。
教材提供“求每个羽毛球的价钱”的情境,让学生感受取商的近似值是实际应用的需要。教材首先让学生理解在解决实际问题时,遇到除不尽的情况,可以取商的近似值。
其次,让学生明白可以根据需要取不同精确度的近似值。如,计算价钱可以精确到“分”,即保留两位小数;也可以精确到“角”,即保留一位小数。
适当补充问题,突出取近似值的意义。小数除法中取近似值有两种情况,一是除不尽的时候;一是除得尽,但是小数位数比较多,根据实际情况不用这么多。例题是在除不尽时的情况下,根据实际需要取近似值。
教材例题解析
例7是教学商从某一位起,一个数字重复出现的情况,为认识循环小数提供感性材料。
教材创设了王鹏赛跑的情境,通过解决问题,引出400÷75。让学生通过实际计算,发现这道题无论除到小数点后面多少位,都除不尽。由此让学生观察这个竖式,看有什么发现。学生会发现余数“25”重复不断出现,商“3”也重复不断出现。
例8通过计算两道除法式题,呈现了除不尽时商的两种情况:一种是从某位起重复出现某一个数字;另一种是从某位起几个数字依次不断重复出现。由此引出循环小数的概念。
引导探究商循环出现的原因
重观察、比较、概括
这里要注意两点:一是结果用“=”;二是适时将算式过程优化。除的过程中,只要余数第二次重复出现,就不必再除,可以确定商。
教材例题解析
在教学“循环小数”概念之后,教材介绍了循环节的概念,给出循环小数的简便记法。
值得注意的是,如果用循环小数表示用“=”连接,如果用近似数表示则用“≈”连接。
教材结合具体算式用“算一算、想一想”的方式组织学生讨论“两个数相除,如果不能得到整数商,所得的商会有哪些情况”,得出两个数相除时商的两种情况,一种是能除尽的情况,商是有限小数;一种是除不尽的情况,商是无限循环小数。在此基础上,介绍有限小数和无限小数的概念。
厘清概念之间的联系。教学有限小数和无限小数的概念时,可以结合大量的实例让学生讨论后明确,如果不能得到整数的商,会有两种情况。由此引出有限小数和无限小数的概念,并说明我们现在学习的小数范围比以前又扩大了,又增加了无限小数,而循环小数就是一种无限小数。但要注意,无限小数除了循环小数外,还有无限不循环小数
教材例题解析
例9教学用计算器探索规律。有三方面的作用:一是巩固循环小数;二是熟练计算器的使用;三是探索规律,但教学重心是规律的探索。
用计算器计算
观察发现规律
利用规律写商
做一做:引导学生观察算式有怎样的规律,可以培养观察的能力。从上往下观察被乘数、乘数是怎样变化的,积是怎样变化的。帮助学生形成观察的方法,分析算式之间的关系。接下来,学生概括表达规律,接写下一个算式,得出一个一般的规律,并进行类推。
教材例题解析
例10是根据实际需要用“进一法”和“去尾法”取商的近似值。
体会根据实际情况用“去尾法”“进一法”取近似值的必要性。由于这两道题算出的结果都是小数,而需要准备的瓶子和包装的礼品盒都必须是整数,因此都要取这些计算结果的近似值。
取近似值时,不能机械地使用“四舍五入”法,要根据具体情况确定“舍”还是“入”。
进一法
去尾法
利用已有经验尝试解决问题,交流体会优化方法
学生可能会有以下几种解法
①0.4×6=2.4(千克)6+1=7(个);
②2.5÷0.4≈6(个)6+1=7(个):③2.5÷0.4=6.25(个)6+1=7(个)
教学实施建议
抓住新旧知识的连接点,在理解算理的基础上,引导学生通过讨论总结小数除法的计算方法。
本单元内容与旧知识联系十分紧密。小数除法的计算法则是以整数除法中被除数和除数同时乘上相同的数(0除外)商不变,以及小数点位置移动规律等知识为基础来说明的。小数除法的试商方法、除的步骤和整数除法基本相同,不同的只是小数点的处理问题。因此,要注意复习和运用整数除法的有关知识,为新知识的学习奠定好基础。
同小数乘法一样,教学中要让学生在理解算理的基础上,及时归纳、总结小数除法的计算方法,帮助学生形成良好的计算能力。
教学实施建议
要注意突出重点,攻破难点。
除数是整数的小数除法,要注意讲明商的小数点为什么与被除数的小数点对齐。小数除以小数,要重点说明除数怎样转化为整数。讲清了一般的计算原理,注意克服难点:小数点的处理问题。学生在计算中经常出现只去掉除数的小数点,而不把被除数的小数点相应地向右移动,或者把小数点的位置移错,使商的小数点常常处理错。为了帮助学生攻破难点,可适当安排有针对性的单项练习。教学中,一方面需要关注要点,重视“除数位数与被除数的小数位数不同”这一除法类型;另一方面,需要加强商中间有0的除法的铺垫与练习,以弥补薄弱,突破难点。
谢谢欣赏
THANK YOU FOR LISTENING
