平面的基本性质

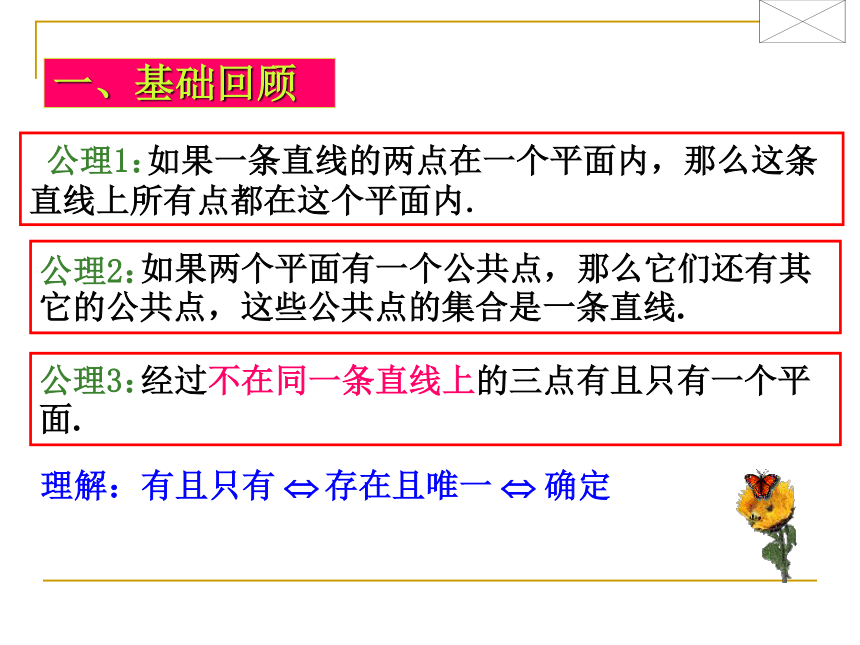
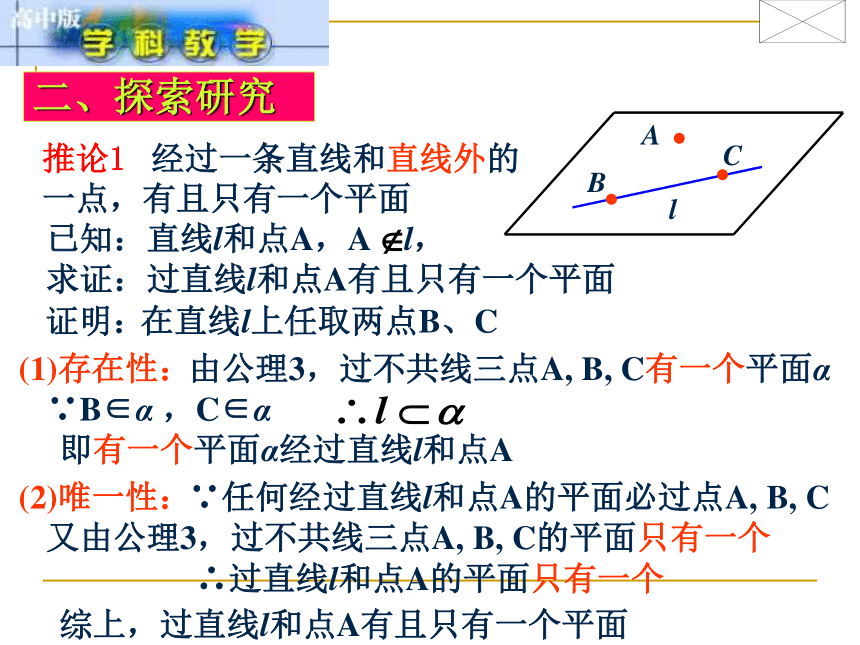
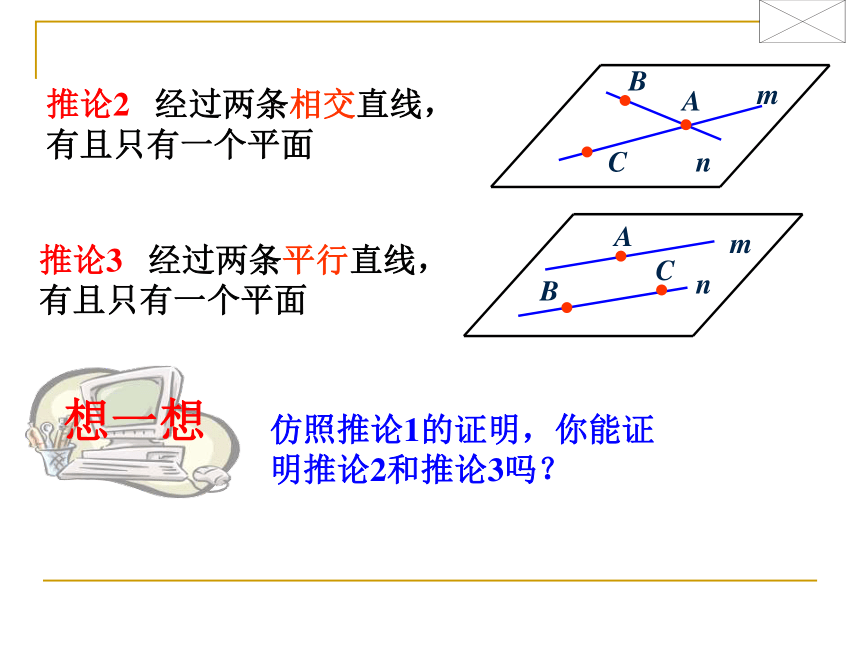
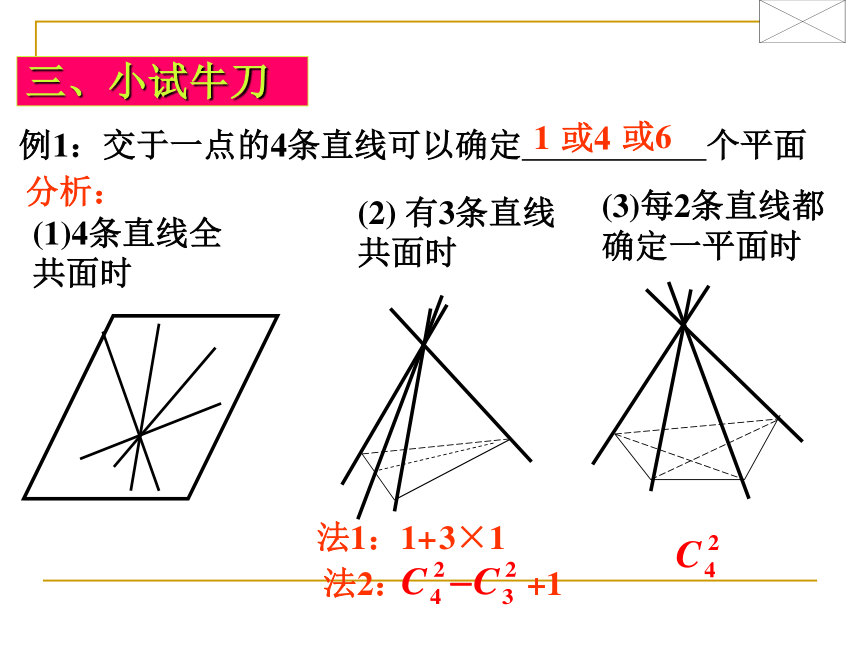
课件12张PPT。9.1平面的基本性质(2) 如果一条直线的两点在一个平面内，那么这条直线上所有点都在这个平面内.一、基础回顾公理1：公理2： 如果两个平面有一个公共点，那么它们还有其它的公共点，这些公共点的集合是一条直线.公理3： 经过不在同一条直线上的三点有且只有一个平面.理解：有且只有 ?存在且唯一? 确定二、探索研究推论1? 经过一条直线和直线外的一点，有且只有一个平面 已知：直线l和点A，A l，求证：过直线l和点A有且只有一个平面B证明：(1)存在性：C在直线l上任取两点B、C由公理3，过不共线三点A, B, C有一个平面α∵B∈α ，C∈α即有一个平面α经过直线l和点A(2)唯一性：∵任何经过直线l和点A的平面必过点A, B, C又由公理3，过不共线三点A, B, C的平面只有一个∴过直线l和点A的平面只有一个 综上，过直线l和点A有且只有一个平面推论2 经过两条相交直线，有且只有一个平面推论3 经过两条平行直线，有且只有一个平面仿照推论1的证明，你能证明推论2和推论3吗？BCABC法2：三、小试牛刀例1：交于一点的4条直线可以确定 个平面(1)4条直线全共面时分析：1(2) 有3条直线共面时法1：1+3×1+1或4(3)每2条直线都确定一平面时或6反馈练习1.三条直线两两相交，由这三条直线所确定平面的
个数是（? ）
A．1??????? B．2??????? C．3???????? D．1或3D2.下列各个条件中，可以确定一个平面的是( )
A.三个点 B.两条不重合的直线
C.一个点和一条直线 D.不共点的两两相交的三条直线 D3.怎样用两根拉紧的细线来检验桌子的四条腿的底端
是否共面？ 四、典例精析例2：求证：两两相交且不过同一点的四条直线共面．已知：直线a、b、c、d两两相交且不过同一点求证：a、b、c、d共面证明：①若有三线共点地情况，如图甲，设b, c, d交于一点D，直线a分别交b, c, d于点A, B, C∵b∩d=D ∴b, d可确定一平面α ∵A∈b，C∈d∴A∈α ，C∈α ∵B∈a，D∈a点评：共面问题的“落入法”先确定一个平面(依据公理3及其3个推论)再证其它的点、线在此平面内(依据公理1)②若无三线共点的情况，如图乙，请你完成证明练习：已知a∥b∥c、a∩l＝B、c∩l ＝C，求证：直线a、b、c、l四线共面证明：∵a//b∴a、b确定一平面α∵b//c∴b、c确定一平面β∵A∈a，B∈b∴A∈α ，B∈α 即 同理 又∵l∩b=B∴由推论2得α 与β重合点评：共面问题的“同一法”先确定多个平面(依据公理3及其3个推论)再证这些平面重合 (证两平面都过可以唯一确定平面的点、线)故直线a、b、c、l四线共面例3：如图点E、F、G、H分别是空间四边形ABCD四边上的点，若直线EF与直线GH交于点Ｐ，求证：Ｂ、Ｄ、Ｐ三点共线．证明：∵P∈EFP∈GH∴P∈面ABD， P∈面BCD即P∈面ABD∩面BCD同理B、D∈面ABD∩面BCD∴由公理2知，Ｂ、Ｄ、Ｐ三点共线点评：共线问题的思路：证各个点都是某两平面的公共点，由公理2得它们共线练习：已知在△ABC在平面α外，AB∩α =P、 AC∩α =Q 、 BC∩α =R ，求证：P、Q、R三点共线。例4：正方体AC1中，E为AB中点，F为AA1中点，(1)求证：E、C、D1、F四点共面(2)求证：CE、D1F 、DA三线交于一点点评：共点问题的思路：先证其中两条线交于一点，再证交点在第三条直线上。(常证它们是梯形两腰) (证第三条直线是两平面的交线，而交点是这两平面的公共点，由公理2得证)练习已知：α∩β=a，β∩γ＝b，α∩γ＝c，b∩c＝p．求证：p∈a．五、小结共面问题法1：“落入法”先确定一个平面(依据公理3及其3个推论)再证其它的点、线在此平面内(依据公理1)法2： “同一法”先确定多个平面(依据公理3及其3个推论)再证这些平面重合 (证两平面都过可以唯一确定平面的点、线)共线问题证各个点都是某两平面的公共点，由公理2得它们共线共点问题先证其中两条线交于一点，再证交点在第三条直线上。(常证它们是梯形两腰) (证第三条直线是两平面的交线，而交点是这两平面的公共点，由公理2得证)种瓜得瓜