3.3 整式 课件(共24张PPT)七年级数学上册北师大版
文档属性
| 名称 | 3.3 整式 课件(共24张PPT)七年级数学上册北师大版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 890.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 14:58:03 | ||
图片预览







文档简介
(共24张PPT)
北师大版 数学 七年级上册
3 整式
第三章 整式及其加减
学习目标
1.通过具体实例理解单项式、多项式、整式的概念.
2.理解单项式的系数、次数,多项式的项数、次数等概念.(重点、难点)
一、导入新课
复习回顾
1.代数式是指用 把数和字母连接起来而形成的式子。
2.列代数式:
(1)原价为a元的书包,现按8折出售,则售价为 元.
(2)甲、乙两人一起在体育场锻炼,体育场跑道每圈400米,甲跑了m圈,乙跑了n圈.甲乙两人共跑了 米.
(3)某种苹果的单价是x元/kg(x<10),用50元买5kg这种苹果,应找回 元.
0.8a
(400m+400n)
(50-5x)
运算符号
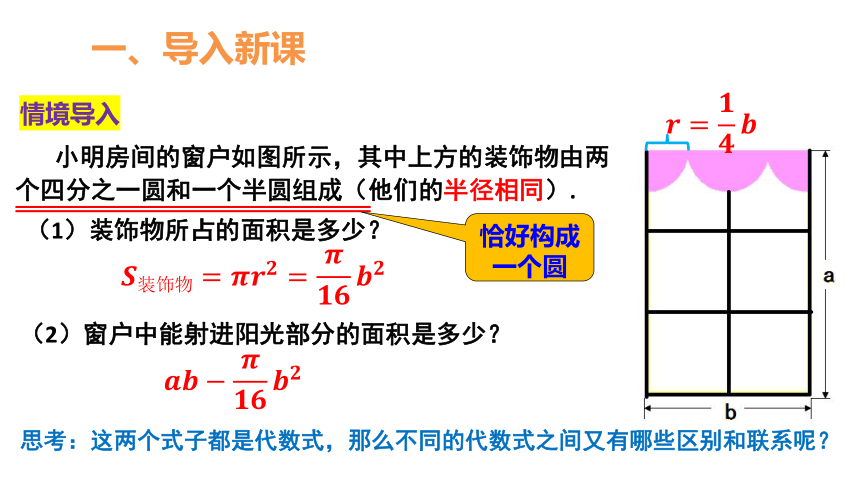
小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(他们的半径相同).
(1)装饰物所占的面积是多少?
一、导入新课
情境导入
(2)窗户中能射进阳光部分的面积是多少?
思考:这两个式子都是代数式,那么不同的代数式之间又有哪些区别和联系呢?
恰好构成一个圆
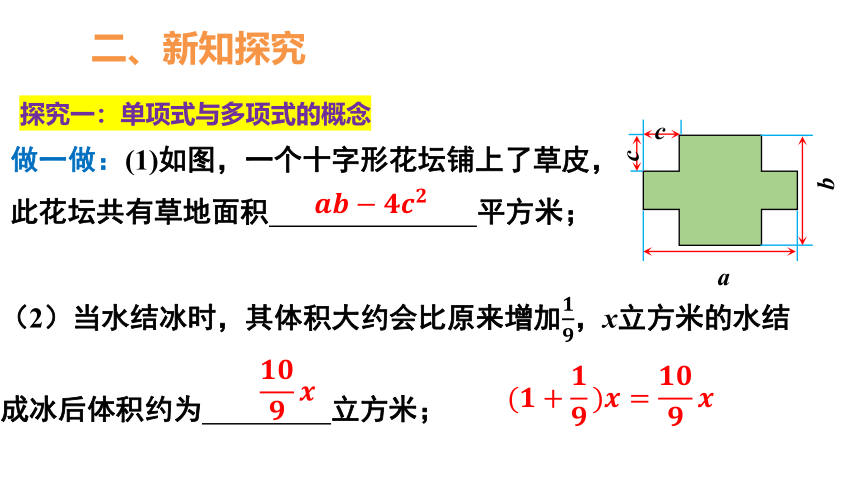
做一做:(1)如图,一个十字形花坛铺上了草皮,此花坛共有草地面积 平方米;
a
b
c
c
(2)当水结冰时,其体积大约会比原来增加,x立方米的水结成冰后体积约为 立方米;
二、新知探究
探究一:单项式与多项式的概念
(4)某件商品成本价为a元,按成本价提高15%后标价又以8折销售,则此件商品的售价为 元。
(3)如图,一个长方体的箱子紧靠墙角,
它的长、宽、高分别是 a,b,c.这个
箱子露在外面的表面积是 ;
二、新知探究
80%(1+15%)a=0.92a
0.92a
ab+ac+bc
观察刚才所列的代数式,你能根据它们的特点分类吗?
二、新知探究
都是数与字母的乘积组成的式子,这样的代数式叫做单项式。
单独一个数或一个字母也是单项式.
例如:像-2,a,-b等是单项式.
0.8a , , , .
想一想:(1)刚才所列的下面这些式子有什么特点?
0.92a
注意:像等不是数字与字母乘积的形式,因此不是单项式.
二、新知探究
上述几个式子都是两个或者多个单项式相加的形式.
几个单项式的和叫做多项式。
400m+400n ,50-5x, , , .
想一想:(2)观察下面这些式子又有什么特点呢?
ab+ac+bc
单项式和多项式统称为整式。
跟踪练习1
x,-3m2,π,-4
x,-3m2,π,-4,
二、新知探究
1.识别单项式的要点:
(1)单项式中不能含有加减运算,不能含有表示大小关系的符号;
(2)单项式的分母中不能含有字母.
2.单项式、多项式、整式的区别与联系:
区别:单项式不含加减运算,多项式必含加减运算.
联系:多项式是几个单项式的和,单项式和多项式都是整式.
二、新知探究
方法归纳
二、新知探究
思考:单项式中的数字和字母各有何意义呢
单项式中的数字因数叫做单项式的系数(包括数字前面的符号).
探究二:单项式和多项式的相关概念
例如:的系数是,
的系数是.
所有字母的指数的和叫做这个单项式的次数.
例如:是2次的,12是4次的.
做一做:判断下列说法是否正确.
①-7xy2的系数是7;( )
②-x2y3的次数是5;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是1.( )
跟踪练习2
二、新知探究
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
单项式的系数包括数字前面的符号
√
二、新知探究
单项式 3a r2
系数
次数
跟踪练习3
写出下列各单项式的系数和次数
3
1
π2
1
3
1
4
-1
3
确定单项式的系数和次数的“两注意”:
(1)单项式的系数:若一个单项式只含有字母因数,则它的系数是1或-1;若单项式是一个常数,则它的系数就是它本身.
(2)单项式的次数是所有字母的指数的和,与系数的指数无关,如24x2y3的次数是5,而不是9.单独一个数的次数是0.
二、新知探究
方法归纳
思考:多项式中的数字和字母各有何意义呢 多项式有没有系数和次数呢?
练一练:多项式的项分别是 ,常数项是 ,它是 次 项式.
二、新知探究
知识要点
多项式有关概念
在多项式中,每个单项式叫做多项式的项(不含字母的项叫做常数项).
一个多项式中,次数最高项的次数就是多项式的次数。
四 三
-5
例如:多项式是与的和.
例如:多项式是2次的,是3次的.
议一议:
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
(1)窗户中能射进阳光的部分的面积分别是多少?
二、新知探究
都是多项式,次数都是2次.
确定多项式的项和次数的“五注意”:
(1)多项式的各项应包括它的符号;
(2)多项式没有“系数”这一概念,但每一项均有系数,每一项的系数应包括它的符号;
(3)一个多项式的最高次项可以不唯一;
(4)区分多项式的次数与单项式的次数,不能误认为多项式的次数是各个单项式的次数之和;
(5)多项式的“项”与“项数”是两个不同的概念,“项”是指组成多项式的单项式,包括它的符号,“项数”是指项的个数.
方法归纳
二、新知探究
三、典例精析
解:单项式:2m,-ab2c,a,-x.多项式:ab+c,ax2+c,y+2.
单项式2m,-ab2c,a,-x的系数分别为2,-1,1,-.多项式ab+c,ax2+c,y+2的次数分别为2,3,1.
三、典例精析
例2:如果多项式3xm-2-(n-1)x+1是关于x的二次二项式,试求m,n的值.
所以m-2=2,n-1=0.
解得:m=4,n=1.
答:m,n的值为m=4,n=1.
解:因为多项式3xm-2-(n-1)x+1是关于x的二次二项式,
四、当堂练习
1.下列说法正确的是( )
A.单项式x的系数和次数都是0 B.34x3是7次单项式
C.5πR2的系数是5 D.0是单项式
D
2.多项式1+2xy-3xy2的次数为( )
A.1 B.2 C.3 D.5
C
5.在多项式中,最高次项的次数是 ,常数项是 。该多项式是 次 项式。
4.多项式2x2-3x+5是________次________项式.
单
3
二
三
四、当堂练习
4
-7
四
三
6.某学校一块长方形绿地的造型如图所示,其中两个扇形表示草坪,两块草坪用五彩石隔开.
(1)求出五彩石部分的面积;
(2)指出(1)中所列的式子是单项式还是多项式,其次数是多少?
四、当堂练习
五、课堂小结
次数:所有字母的指数的和.
系数:单项式中的数字因数.
次数:多项式中次数最高的项的次数.
项:多项式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
通过本节课的学习,你有什么收获?
整式
六、作业布置
习题3.4
北师大版 数学 七年级上册
3 整式
第三章 整式及其加减
学习目标
1.通过具体实例理解单项式、多项式、整式的概念.
2.理解单项式的系数、次数,多项式的项数、次数等概念.(重点、难点)
一、导入新课
复习回顾
1.代数式是指用 把数和字母连接起来而形成的式子。
2.列代数式:
(1)原价为a元的书包,现按8折出售,则售价为 元.
(2)甲、乙两人一起在体育场锻炼,体育场跑道每圈400米,甲跑了m圈,乙跑了n圈.甲乙两人共跑了 米.
(3)某种苹果的单价是x元/kg(x<10),用50元买5kg这种苹果,应找回 元.
0.8a
(400m+400n)
(50-5x)
运算符号
小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(他们的半径相同).
(1)装饰物所占的面积是多少?
一、导入新课
情境导入
(2)窗户中能射进阳光部分的面积是多少?
思考:这两个式子都是代数式,那么不同的代数式之间又有哪些区别和联系呢?
恰好构成一个圆
做一做:(1)如图,一个十字形花坛铺上了草皮,此花坛共有草地面积 平方米;
a
b
c
c
(2)当水结冰时,其体积大约会比原来增加,x立方米的水结成冰后体积约为 立方米;
二、新知探究
探究一:单项式与多项式的概念
(4)某件商品成本价为a元,按成本价提高15%后标价又以8折销售,则此件商品的售价为 元。
(3)如图,一个长方体的箱子紧靠墙角,
它的长、宽、高分别是 a,b,c.这个
箱子露在外面的表面积是 ;
二、新知探究
80%(1+15%)a=0.92a
0.92a
ab+ac+bc
观察刚才所列的代数式,你能根据它们的特点分类吗?
二、新知探究
都是数与字母的乘积组成的式子,这样的代数式叫做单项式。
单独一个数或一个字母也是单项式.
例如:像-2,a,-b等是单项式.
0.8a , , , .
想一想:(1)刚才所列的下面这些式子有什么特点?
0.92a
注意:像等不是数字与字母乘积的形式,因此不是单项式.
二、新知探究
上述几个式子都是两个或者多个单项式相加的形式.
几个单项式的和叫做多项式。
400m+400n ,50-5x, , , .
想一想:(2)观察下面这些式子又有什么特点呢?
ab+ac+bc
单项式和多项式统称为整式。
跟踪练习1
x,-3m2,π,-4
x,-3m2,π,-4,
二、新知探究
1.识别单项式的要点:
(1)单项式中不能含有加减运算,不能含有表示大小关系的符号;
(2)单项式的分母中不能含有字母.
2.单项式、多项式、整式的区别与联系:
区别:单项式不含加减运算,多项式必含加减运算.
联系:多项式是几个单项式的和,单项式和多项式都是整式.
二、新知探究
方法归纳
二、新知探究
思考:单项式中的数字和字母各有何意义呢
单项式中的数字因数叫做单项式的系数(包括数字前面的符号).
探究二:单项式和多项式的相关概念
例如:的系数是,
的系数是.
所有字母的指数的和叫做这个单项式的次数.
例如:是2次的,12是4次的.
做一做:判断下列说法是否正确.
①-7xy2的系数是7;( )
②-x2y3的次数是5;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是1.( )
跟踪练习2
二、新知探究
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
单项式的系数包括数字前面的符号
√
二、新知探究
单项式 3a r2
系数
次数
跟踪练习3
写出下列各单项式的系数和次数
3
1
π2
1
3
1
4
-1
3
确定单项式的系数和次数的“两注意”:
(1)单项式的系数:若一个单项式只含有字母因数,则它的系数是1或-1;若单项式是一个常数,则它的系数就是它本身.
(2)单项式的次数是所有字母的指数的和,与系数的指数无关,如24x2y3的次数是5,而不是9.单独一个数的次数是0.
二、新知探究
方法归纳
思考:多项式中的数字和字母各有何意义呢 多项式有没有系数和次数呢?
练一练:多项式的项分别是 ,常数项是 ,它是 次 项式.
二、新知探究
知识要点
多项式有关概念
在多项式中,每个单项式叫做多项式的项(不含字母的项叫做常数项).
一个多项式中,次数最高项的次数就是多项式的次数。
四 三
-5
例如:多项式是与的和.
例如:多项式是2次的,是3次的.
议一议:
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
(1)窗户中能射进阳光的部分的面积分别是多少?
二、新知探究
都是多项式,次数都是2次.
确定多项式的项和次数的“五注意”:
(1)多项式的各项应包括它的符号;
(2)多项式没有“系数”这一概念,但每一项均有系数,每一项的系数应包括它的符号;
(3)一个多项式的最高次项可以不唯一;
(4)区分多项式的次数与单项式的次数,不能误认为多项式的次数是各个单项式的次数之和;
(5)多项式的“项”与“项数”是两个不同的概念,“项”是指组成多项式的单项式,包括它的符号,“项数”是指项的个数.
方法归纳
二、新知探究
三、典例精析
解:单项式:2m,-ab2c,a,-x.多项式:ab+c,ax2+c,y+2.
单项式2m,-ab2c,a,-x的系数分别为2,-1,1,-.多项式ab+c,ax2+c,y+2的次数分别为2,3,1.
三、典例精析
例2:如果多项式3xm-2-(n-1)x+1是关于x的二次二项式,试求m,n的值.
所以m-2=2,n-1=0.
解得:m=4,n=1.
答:m,n的值为m=4,n=1.
解:因为多项式3xm-2-(n-1)x+1是关于x的二次二项式,
四、当堂练习
1.下列说法正确的是( )
A.单项式x的系数和次数都是0 B.34x3是7次单项式
C.5πR2的系数是5 D.0是单项式
D
2.多项式1+2xy-3xy2的次数为( )
A.1 B.2 C.3 D.5
C
5.在多项式中,最高次项的次数是 ,常数项是 。该多项式是 次 项式。
4.多项式2x2-3x+5是________次________项式.
单
3
二
三
四、当堂练习
4
-7
四
三
6.某学校一块长方形绿地的造型如图所示,其中两个扇形表示草坪,两块草坪用五彩石隔开.
(1)求出五彩石部分的面积;
(2)指出(1)中所列的式子是单项式还是多项式,其次数是多少?
四、当堂练习
五、课堂小结
次数:所有字母的指数的和.
系数:单项式中的数字因数.
次数:多项式中次数最高的项的次数.
项:多项式中的每个单项式叫多项式的项.
(其中不含字母的项叫做常数项)
通过本节课的学习,你有什么收获?
整式
六、作业布置
习题3.4
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
