圆解决问题拔尖特训专项训练(含答案)数学六年级上册北师大版
文档属性
| 名称 | 圆解决问题拔尖特训专项训练(含答案)数学六年级上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 21:01:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆解决问题拔尖特训(专项训练)数学六年级上册北师大版
1.一只大钟,它的分针长40厘米。当从1时到2时,这根分针的尖端所走的路程是多少厘米?分针扫过的面积是多少平方厘米?
2.一个半圆形花坛的周长是25.7米,它的面积是多少平方米?
3.如图,圆的面积和长方形的面积相等,如果圆的半径是6厘米,那么长方形的周长是多少厘米?
4.如图所示,圆内有一个最大的正方形,已知正方形的面积为40平方厘米,求阴影部分的面积是多少平方厘米?
5.某小学为提升校园环境,新建了一个半径为3米的圆形花坛,在这个花坛周围铺上一条1米宽的鹅卵石路,如果铺每平方米鹅卵石路需要50元,铺完这条鹅卵石路共需要多少元?
6.张明以每分钟157米的速度沿着圆形场地的边跑了一圈,正好用了10分钟,这个圆形场地的占地面积是多少平方米?
7.一个圆形花坛的半径是3米,现在要扩建花坛,将半径增加1米,这时花坛的占地面积增加了多少平方米?
8.校园里有一个花坛(如图),它的中心是一个边长为5m的正方形,周围是4个半圆,这个花坛的周长是多少米?面积是多少平方米?
9.笑笑准备用一个长62.8厘米的铁线围成一个图形,围成什么图形面积最大?试着算出你围成图形的面积。
10.草地上有一个木桩,把一头牛用绳拴在木桩上,若绳子长4米,这头牛最多可以吃到多少平方米的草?
11.如图,正方形里画了一个最大的圆。已知正方形的面积是16平方分米,那么圆的面积是多少平方分米?
12.自行车转动问题。一辆自行车的外轮车轮直径是50厘米,如果每分钟转50周,要通过一座942米长的桥,需要多少分钟?
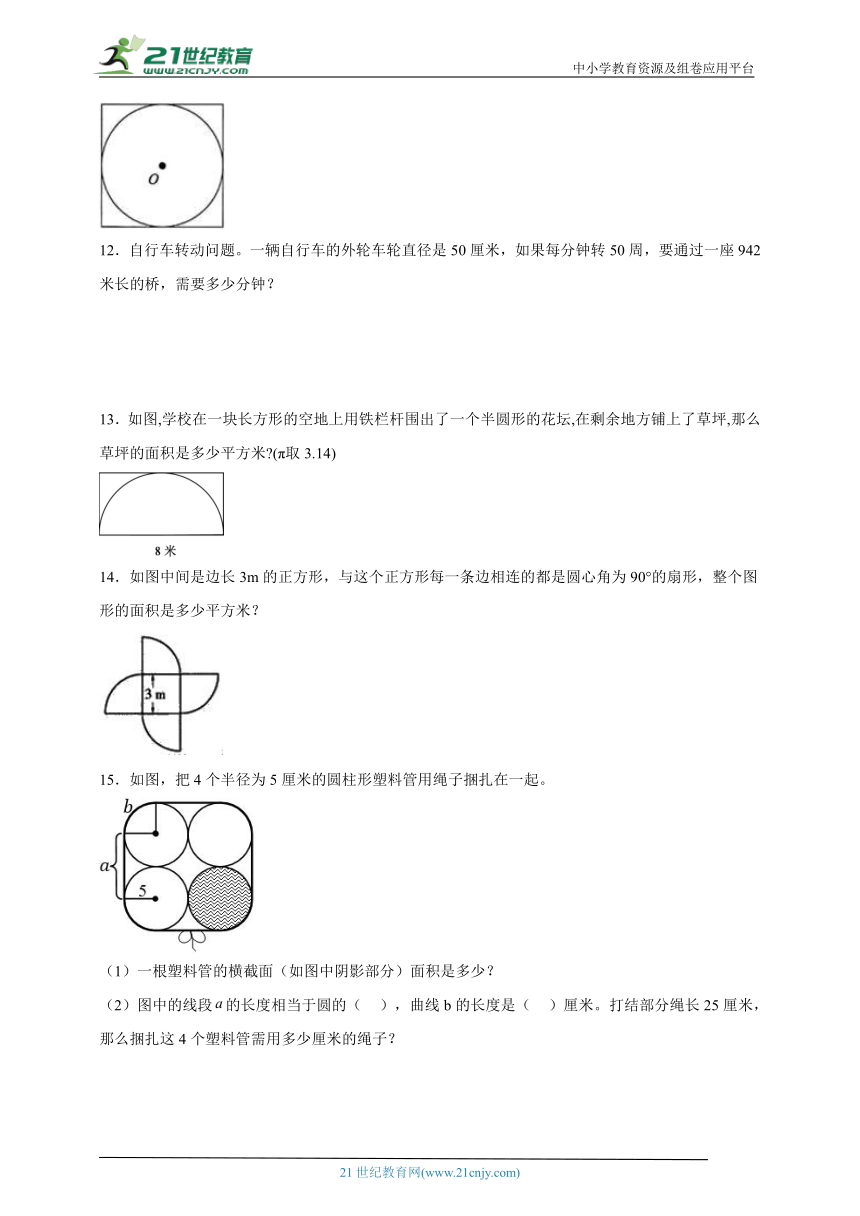
13.如图,学校在一块长方形的空地上用铁栏杆围出了一个半圆形的花坛,在剩余地方铺上了草坪,那么草坪的面积是多少平方米 (π取3.14)
14.如图中间是边长3m的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,整个图形的面积是多少平方米?
15.如图,把4个半径为5厘米的圆柱形塑料管用绳子捆扎在一起。
(1)一根塑料管的横截面(如图中阴影部分)面积是多少?
(2)图中的线段的长度相当于圆的( ),曲线b的长度是( )厘米。打结部分绳长25厘米,那么捆扎这4个塑料管需用多少厘米的绳子?
16.如图,两个连在一起的皮带轮,已知小轮的半径是3分米,当这个小轮转4周时,大轮正好转1周。这个大轮的半径是多少分米?
参考答案:
1.251.2厘米;
5024平方厘米
【分析】根据题干:一只大钟,它的分针长40厘米,可知分针的尖端转动一周所走的路程正好是以分针的长度为半径的圆的周长,利用圆周长的计算公式计算即可;
从1时到2时分针扫过的面积是半径是40厘米的圆的面积,根据圆的面积公式解答。
【详解】已知r=40厘米
2×3.14×40=251.2(厘米)
答:这根分针的尖端所走的路程是251.2厘米。
3.14×402=5024(平方厘米)
答:分针扫过的面积是5024平方厘米。
【点睛】此题考查圆的周长与面积公式的应用,关键是根据钟面上分针旋转的特点得出旋转后的图形。
2.39.25平方米
【分析】由题意知,花坛是半圆形,要求它的面积,需先求得半径;已知这个花坛的周长是25.7米,依据半圆的周长=πr+2r=(π+2)r,可知半圆的半径等于半圆的周长除以(π+2),因此用25.7÷(π+2)求得半径,再利用S半圆=πr2÷2求得面积即可。
【详解】半圆形花坛的半径为:
25.7÷(π+2)
=25.7÷(3.14+2)
=25.7÷5.14
=5(米)
面积为:
3.14×52÷2
=78.5÷2
=39.25(平方米)
答:它的面积是39.25平方米。
【点睛】此题考查了半圆的周长公式以及面积公式的灵活应用。
3.49.68厘米
【分析】根据题意可知,长方形的宽等于圆的半径,长方形的长等于圆周长的一半,已知圆的周长C=2πr,据此解答。
【详解】2×3.14×6÷2
=3.14×6
=18.84(厘米)
(18.84+6)×2
=24.84×2
=49.68(厘米)
答:长方形的周长是49.68平方厘米。
【点睛】此题考查了圆的周长计算,明确圆和长方形之间的关系是解题关键。
4.22.8平方厘米
【分析】根据题意可知,如图圆内正方形面积是40平方厘米,正方形面积=圆的直径×圆的半径;直径=2×半径;正方形面积=2×半径2,由此可知,圆的半径2=正方形面积÷2;圆的面积=π×半径2;代入数据,求出圆的面积,再用圆的面积-正方形的面积,求出阴影部分面积,即可解答。
【详解】3.14×(40÷2)-40
=3.14×20-40
=62.8-40
=22.8(平方厘米)
答:阴影部分的面积是22.8平方厘米。
【点睛】利用正方形面积公式,圆的公式进行解答,关键明确正方形的面积与圆的半径平方之间的关系。
5.1099元
【分析】根据题意可知鹅卵石路的面积是环形面积,根据环形面积公式:S=π(R2-r2),把数据代入可求出鹅卵石路的面积,然后用所求面积乘每平方米鹅卵石路需要的价钱,即可解答。
【详解】3.14×(3+1)2-3.14×32
=3.14×16-3.14×9
=50.24-28.26
=21.98(平方米)
21.98×50=1099(元)
答:铺完这条鹅卵石路共需要1099元。
【点睛】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
6.196250平方米
【分析】张明跑了一圈走的路程就是圆形场地的周长,先根据路程=速度×时间,求出路程,也就是圆的周长,根据半径=周长÷圆周率÷2,求出圆形场地的半径,再根据面积=πr2即可解答。
【详解】157×10=1570(米)
1570÷3.14÷2=250(米)
3.14×2502=196250(平方米)
答:它的占地面积是196250平方米。
【点睛】本题主要考查学生依据求圆的面积和周长的方法,解决问题的能力。
7.21.98平方米
【详解】(3+1)×(3+1)×3.14 3×3×3.14
=16×3.14 9×3.14
=21.98(平方米)
8.周长:31.4米,面积:64.25平方米.
【详解】周长:3.14×5×2=31.4 (m)
面积:3.14×()2×2+5×5 =64.25 (m2)
答:这个花坛的周长是31.4米,面积是64.25平方米.
9.圆形;314平方厘米
【分析】周长相等的长方形、正方形和圆,圆的面积最大,根据圆的周长公式,周长=π×2×半径;求出圆的半径;再根据圆的面积公式:π×半径2,代入数据,求出面积。
【详解】周长相等的长方形、正方形和圆中,圆的面积最大。
半径:62.8÷3.14÷2
=20÷2
=10(厘米)
面积:3.14×102
=3.14×100
=314(平方厘米)
答:围成的圆的面积最大;面积是314平方厘米。
【点睛】本题考查圆的周长公式、面积公式的应用,关键明确,在周长相等的长方形、正方形和圆中,圆的面积最大。
10.50.24平方米
【分析】根据圆的面积公式:面积=π×半径2,代入数据,求出半径是4米的圆的面积,也就是牛最多可以吃到多少平方米的草,据此解答。
【详解】3.14×42
=3.14×16
=50.24(平方米)
答:这头牛最多可以吃到50.24平方米的草。
【点睛】熟练掌握圆的面积公式是解答本题的关键。
11.12.56平方分米
【分析】通过观察图形可知,正方形的边长等于圆的半径的2倍,根据正方形的面积=边长×边长,已知正方形的面积可以求出半径的平方,再根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】解:设圆的半径为r分米,
2r×2r=16
4r2=16
r2=4
3.14×4=12.56(平方分米)
答:这个圆的面积是12.56平方分米。
【点睛】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
12.12分钟
【分析】首先根据圆的周长公式:C=πd,求出车轮的周长,用车轮的周长乘每分钟转的周数求出每分钟的速度,然后根据时间=路程÷速度,据此列式解答。
【详解】50厘米=0.5米
942÷(3.14×0.5×50)
=942÷78.5
=12(分钟)
答:需要12分钟。
【点睛】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式。
13.6.88平方米
【解析】略
14.37.26平方米
【详解】3×3+3.14×32
=9+28.26
=37.26(平方米)
答:整个图形的面积是37.26平方米.
15.(1)78.5平方厘米;(2)直径;7.85;96.4厘米
【分析】(1)一根塑料管的横截面面积是半径为5cm的圆的面积,然后再根据圆的面积公式S=πr2进行解答。
(2)图中的线段的长度相当于圆的直径,曲线b的长度相当于半径为5cm的圆的周长;捆扎这4个塑料管的绳子长度=半径为5cm的圆的周长+圆的直径×4+打结部分绳长;然后再根据圆的周长公式C=2πr,d=2r进行解答。
【详解】(1)3.14×52
=3.14×25
=78.5(平方厘米)
答:一根塑料管的横截面(如图中阴影部分)面积是78.5平方厘米。
(2)2×3.14×5×
=6.28×5×
=31.4×
=7.85(厘米)
即图中的线段的长度相当于圆的直径,曲线b的长度是7.85厘米。
2×3.14×5+2×5×4+25
=6.28×5+10×4+25
=31.4+40+25
=71.4+25
=96.4(厘米)
答:那么捆扎这4个塑料管需用96.4厘米的绳子。
【点睛】考查了圆的面积公式和周长公式的运用。
16.12分米
【分析】根据题意可知,大小两个轮子转过的距离是相等的,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】2×3.14×3×4÷(2×3.14)
=18.84×4÷6.28
=75.36÷6.28
=12(分米)
答:这个大轮的半径是12分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆解决问题拔尖特训(专项训练)数学六年级上册北师大版
1.一只大钟,它的分针长40厘米。当从1时到2时,这根分针的尖端所走的路程是多少厘米?分针扫过的面积是多少平方厘米?
2.一个半圆形花坛的周长是25.7米,它的面积是多少平方米?
3.如图,圆的面积和长方形的面积相等,如果圆的半径是6厘米,那么长方形的周长是多少厘米?
4.如图所示,圆内有一个最大的正方形,已知正方形的面积为40平方厘米,求阴影部分的面积是多少平方厘米?
5.某小学为提升校园环境,新建了一个半径为3米的圆形花坛,在这个花坛周围铺上一条1米宽的鹅卵石路,如果铺每平方米鹅卵石路需要50元,铺完这条鹅卵石路共需要多少元?
6.张明以每分钟157米的速度沿着圆形场地的边跑了一圈,正好用了10分钟,这个圆形场地的占地面积是多少平方米?
7.一个圆形花坛的半径是3米,现在要扩建花坛,将半径增加1米,这时花坛的占地面积增加了多少平方米?
8.校园里有一个花坛(如图),它的中心是一个边长为5m的正方形,周围是4个半圆,这个花坛的周长是多少米?面积是多少平方米?
9.笑笑准备用一个长62.8厘米的铁线围成一个图形,围成什么图形面积最大?试着算出你围成图形的面积。
10.草地上有一个木桩,把一头牛用绳拴在木桩上,若绳子长4米,这头牛最多可以吃到多少平方米的草?
11.如图,正方形里画了一个最大的圆。已知正方形的面积是16平方分米,那么圆的面积是多少平方分米?
12.自行车转动问题。一辆自行车的外轮车轮直径是50厘米,如果每分钟转50周,要通过一座942米长的桥,需要多少分钟?
13.如图,学校在一块长方形的空地上用铁栏杆围出了一个半圆形的花坛,在剩余地方铺上了草坪,那么草坪的面积是多少平方米 (π取3.14)
14.如图中间是边长3m的正方形,与这个正方形每一条边相连的都是圆心角为90°的扇形,整个图形的面积是多少平方米?
15.如图,把4个半径为5厘米的圆柱形塑料管用绳子捆扎在一起。
(1)一根塑料管的横截面(如图中阴影部分)面积是多少?
(2)图中的线段的长度相当于圆的( ),曲线b的长度是( )厘米。打结部分绳长25厘米,那么捆扎这4个塑料管需用多少厘米的绳子?
16.如图,两个连在一起的皮带轮,已知小轮的半径是3分米,当这个小轮转4周时,大轮正好转1周。这个大轮的半径是多少分米?
参考答案:
1.251.2厘米;
5024平方厘米
【分析】根据题干:一只大钟,它的分针长40厘米,可知分针的尖端转动一周所走的路程正好是以分针的长度为半径的圆的周长,利用圆周长的计算公式计算即可;
从1时到2时分针扫过的面积是半径是40厘米的圆的面积,根据圆的面积公式解答。
【详解】已知r=40厘米
2×3.14×40=251.2(厘米)
答:这根分针的尖端所走的路程是251.2厘米。
3.14×402=5024(平方厘米)
答:分针扫过的面积是5024平方厘米。
【点睛】此题考查圆的周长与面积公式的应用,关键是根据钟面上分针旋转的特点得出旋转后的图形。
2.39.25平方米
【分析】由题意知,花坛是半圆形,要求它的面积,需先求得半径;已知这个花坛的周长是25.7米,依据半圆的周长=πr+2r=(π+2)r,可知半圆的半径等于半圆的周长除以(π+2),因此用25.7÷(π+2)求得半径,再利用S半圆=πr2÷2求得面积即可。
【详解】半圆形花坛的半径为:
25.7÷(π+2)
=25.7÷(3.14+2)
=25.7÷5.14
=5(米)
面积为:
3.14×52÷2
=78.5÷2
=39.25(平方米)
答:它的面积是39.25平方米。
【点睛】此题考查了半圆的周长公式以及面积公式的灵活应用。
3.49.68厘米
【分析】根据题意可知,长方形的宽等于圆的半径,长方形的长等于圆周长的一半,已知圆的周长C=2πr,据此解答。
【详解】2×3.14×6÷2
=3.14×6
=18.84(厘米)
(18.84+6)×2
=24.84×2
=49.68(厘米)
答:长方形的周长是49.68平方厘米。
【点睛】此题考查了圆的周长计算,明确圆和长方形之间的关系是解题关键。
4.22.8平方厘米
【分析】根据题意可知,如图圆内正方形面积是40平方厘米,正方形面积=圆的直径×圆的半径;直径=2×半径;正方形面积=2×半径2,由此可知,圆的半径2=正方形面积÷2;圆的面积=π×半径2;代入数据,求出圆的面积,再用圆的面积-正方形的面积,求出阴影部分面积,即可解答。
【详解】3.14×(40÷2)-40
=3.14×20-40
=62.8-40
=22.8(平方厘米)
答:阴影部分的面积是22.8平方厘米。
【点睛】利用正方形面积公式,圆的公式进行解答,关键明确正方形的面积与圆的半径平方之间的关系。
5.1099元
【分析】根据题意可知鹅卵石路的面积是环形面积,根据环形面积公式:S=π(R2-r2),把数据代入可求出鹅卵石路的面积,然后用所求面积乘每平方米鹅卵石路需要的价钱,即可解答。
【详解】3.14×(3+1)2-3.14×32
=3.14×16-3.14×9
=50.24-28.26
=21.98(平方米)
21.98×50=1099(元)
答:铺完这条鹅卵石路共需要1099元。
【点睛】此题主要考查环形面积公式的灵活运用,关键是熟记公式。
6.196250平方米
【分析】张明跑了一圈走的路程就是圆形场地的周长,先根据路程=速度×时间,求出路程,也就是圆的周长,根据半径=周长÷圆周率÷2,求出圆形场地的半径,再根据面积=πr2即可解答。
【详解】157×10=1570(米)
1570÷3.14÷2=250(米)
3.14×2502=196250(平方米)
答:它的占地面积是196250平方米。
【点睛】本题主要考查学生依据求圆的面积和周长的方法,解决问题的能力。
7.21.98平方米
【详解】(3+1)×(3+1)×3.14 3×3×3.14
=16×3.14 9×3.14
=21.98(平方米)
8.周长:31.4米,面积:64.25平方米.
【详解】周长:3.14×5×2=31.4 (m)
面积:3.14×()2×2+5×5 =64.25 (m2)
答:这个花坛的周长是31.4米,面积是64.25平方米.
9.圆形;314平方厘米
【分析】周长相等的长方形、正方形和圆,圆的面积最大,根据圆的周长公式,周长=π×2×半径;求出圆的半径;再根据圆的面积公式:π×半径2,代入数据,求出面积。
【详解】周长相等的长方形、正方形和圆中,圆的面积最大。
半径:62.8÷3.14÷2
=20÷2
=10(厘米)
面积:3.14×102
=3.14×100
=314(平方厘米)
答:围成的圆的面积最大;面积是314平方厘米。
【点睛】本题考查圆的周长公式、面积公式的应用,关键明确,在周长相等的长方形、正方形和圆中,圆的面积最大。
10.50.24平方米
【分析】根据圆的面积公式:面积=π×半径2,代入数据,求出半径是4米的圆的面积,也就是牛最多可以吃到多少平方米的草,据此解答。
【详解】3.14×42
=3.14×16
=50.24(平方米)
答:这头牛最多可以吃到50.24平方米的草。
【点睛】熟练掌握圆的面积公式是解答本题的关键。
11.12.56平方分米
【分析】通过观察图形可知,正方形的边长等于圆的半径的2倍,根据正方形的面积=边长×边长,已知正方形的面积可以求出半径的平方,再根据圆的面积公式:S=πr2,把数据代入公式解答。
【详解】解:设圆的半径为r分米,
2r×2r=16
4r2=16
r2=4
3.14×4=12.56(平方分米)
答:这个圆的面积是12.56平方分米。
【点睛】此题主要考查正方形的面积公式、圆的面积公式的灵活运用,关键是熟记公式。
12.12分钟
【分析】首先根据圆的周长公式:C=πd,求出车轮的周长,用车轮的周长乘每分钟转的周数求出每分钟的速度,然后根据时间=路程÷速度,据此列式解答。
【详解】50厘米=0.5米
942÷(3.14×0.5×50)
=942÷78.5
=12(分钟)
答:需要12分钟。
【点睛】此题主要考查圆的周长公式在实际生活中的应用,关键是熟记公式。
13.6.88平方米
【解析】略
14.37.26平方米
【详解】3×3+3.14×32
=9+28.26
=37.26(平方米)
答:整个图形的面积是37.26平方米.
15.(1)78.5平方厘米;(2)直径;7.85;96.4厘米
【分析】(1)一根塑料管的横截面面积是半径为5cm的圆的面积,然后再根据圆的面积公式S=πr2进行解答。
(2)图中的线段的长度相当于圆的直径,曲线b的长度相当于半径为5cm的圆的周长;捆扎这4个塑料管的绳子长度=半径为5cm的圆的周长+圆的直径×4+打结部分绳长;然后再根据圆的周长公式C=2πr,d=2r进行解答。
【详解】(1)3.14×52
=3.14×25
=78.5(平方厘米)
答:一根塑料管的横截面(如图中阴影部分)面积是78.5平方厘米。
(2)2×3.14×5×
=6.28×5×
=31.4×
=7.85(厘米)
即图中的线段的长度相当于圆的直径,曲线b的长度是7.85厘米。
2×3.14×5+2×5×4+25
=6.28×5+10×4+25
=31.4+40+25
=71.4+25
=96.4(厘米)
答:那么捆扎这4个塑料管需用96.4厘米的绳子。
【点睛】考查了圆的面积公式和周长公式的运用。
16.12分米
【分析】根据题意可知,大小两个轮子转过的距离是相等的,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】2×3.14×3×4÷(2×3.14)
=18.84×4÷6.28
=75.36÷6.28
=12(分米)
答:这个大轮的半径是12分米。
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
