2.2基本不等式 课件(共21张PPT)
文档属性
| 名称 | 2.2基本不等式 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 17:37:43 | ||
图片预览








文档简介
(共21张PPT)
2.2基本不等式
教学目标
1. 结合实例,从情境中抽象、归纳出算术平均数和几何平均数的概念,从特殊到一般猜想、发现基本不等式.
2. 通过对基本不等式几何意义的探究,感受数学文化之美,体会数形结合的魅力.
3. 探索基本不等式的证明过程,学会用作差法、综合法、分析法证明基本不等式.
学习目标
课程目标 学科核心素养
理解、掌握基本不等式的内容和结构 通过由完全平方公式到基本不等式的过程,培养逻辑推理素养
能够利用不等式的性质证明基本不等式,初步理解分析法的证明方法 借助基本不等式的证明过程,培养逻辑推理、数学运算素养
复习回顾
问题1 什么是不等式的最基本性质?
;
;
作差法:要比较两个实数的大小,可以转化为比较它们的差与0的大小
复习回顾
性质 别名 性质内容 注意
1 对称性 a>b b2 传递性 a>b,b>c a>c 不可逆
3 可加性 a>b a+c>b+c 可逆
4 可乘性 a>b,c>0 ac>bc a>b,c<0 ac5 同向可加性 a>b,c>d a+c>b+d 同向可加
6 同向同正可乘性 a>b>0,c>d>0 ac>bd 正值同向可乘
7 可乘方性 a>b>0 an>bn(n∈N,n≥2) 正值同向可乘方
问题2 什么是不等式的基本性质?
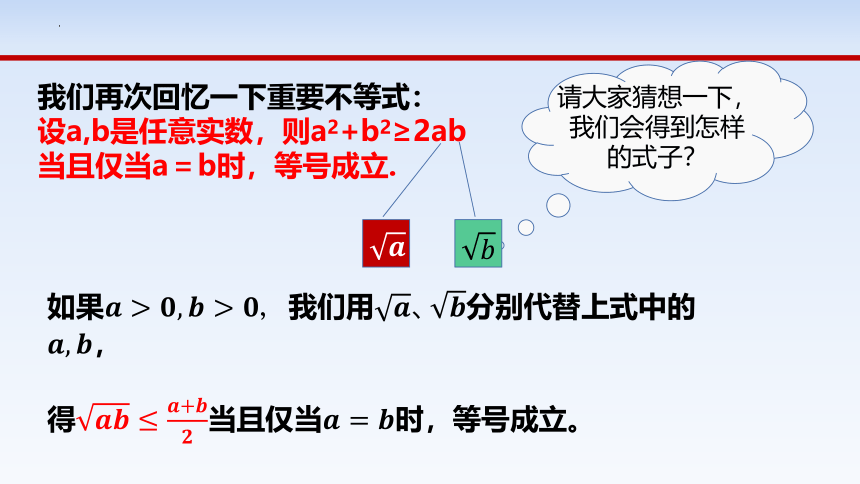
我们再次回忆一下重要不等式:
设a,b是任意实数,则a2+b2≥2ab
当且仅当a=b时,等号成立.
请大家猜想一下,我们会得到怎样的式子?
如果我们用分别代替上式中的,
得当且仅当时,等号成立。
如果我们用分别代替上式中的,可得
当且仅当时,等号成立。这样的式子为基本不等式
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
叫做正数的算术平均数
叫做正数 的几何平均数
新课讲授
上面通过考察的特殊情形获得了基本不等式。能否直接利用不等式的性质推导出基本不等式呢?下面我们来分析一下。
新课讲授
要证:①
只要证:②
要证②,只要证: ③
要证③,只要证:④
要证④,只要证:
显然,⑤成立,当且仅当a=b时,⑤中的等号成立。
只要把上述过程倒过来,就能直接推出基本不等式了。
如图,可证 因而由于小于或等于圆的半径,用不等式表示为.
显然,当且仅当点与圆心重合,即当时,上述不等式的等号成立.
基本不等式的几何意义
例1.已知x,y都是正数,求证:
(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值
探究一 对基本不等式的理解
例1.已知x,y都是正数,求证:
(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值
探究一 对基本不等式的理解
总结:和定积最大,积定和最小
探究二 和定积最大,积定和最小
例2 求函数 的最小值,并求出y取得最小值时x的值。
一正:符合基本不等式 成立的前提条件,a>0,b>0
二定:化不等式的一边为定值(a+b为定值或ab为定值)
三相等:必须存在“=”成立的条件
小结--基本不等式求最值问题
一正、二定、三相等!!!!!!
和定积最大,积定和最小
【例】已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
【证明】所以
(1)等于定值P时, ,所以
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,所以
,当且仅当时,上式等号成立,此时有最大值
最值定理及其应用
①当时,,,
当且仅当时,等号成立.
②当时,,
当且仅当时,等号成立.
最值定理及其应用
基本不等式
利用基本不等式求最值的条件:
一正、二定、三相等。
基本不等式
基本不等式
3.已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
证明:所以
(1)等于定值P时, ,∴
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,
当且仅当时,上式等号成立,此时有最大值
课堂小结
通常称不等式(1)为基本不等式,其中,叫做正数a,b的算术平均数,正数a,b的几何平均数。
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
即:
谢谢学习
Thank you for learning
2.2基本不等式
教学目标
1. 结合实例,从情境中抽象、归纳出算术平均数和几何平均数的概念,从特殊到一般猜想、发现基本不等式.
2. 通过对基本不等式几何意义的探究,感受数学文化之美,体会数形结合的魅力.
3. 探索基本不等式的证明过程,学会用作差法、综合法、分析法证明基本不等式.
学习目标
课程目标 学科核心素养
理解、掌握基本不等式的内容和结构 通过由完全平方公式到基本不等式的过程,培养逻辑推理素养
能够利用不等式的性质证明基本不等式,初步理解分析法的证明方法 借助基本不等式的证明过程,培养逻辑推理、数学运算素养
复习回顾
问题1 什么是不等式的最基本性质?
;
;
作差法:要比较两个实数的大小,可以转化为比较它们的差与0的大小
复习回顾
性质 别名 性质内容 注意
1 对称性 a>b b2 传递性 a>b,b>c a>c 不可逆
3 可加性 a>b a+c>b+c 可逆
4 可乘性 a>b,c>0 ac>bc a>b,c<0 ac
6 同向同正可乘性 a>b>0,c>d>0 ac>bd 正值同向可乘
7 可乘方性 a>b>0 an>bn(n∈N,n≥2) 正值同向可乘方
问题2 什么是不等式的基本性质?
我们再次回忆一下重要不等式:
设a,b是任意实数,则a2+b2≥2ab
当且仅当a=b时,等号成立.
请大家猜想一下,我们会得到怎样的式子?
如果我们用分别代替上式中的,
得当且仅当时,等号成立。
如果我们用分别代替上式中的,可得
当且仅当时,等号成立。这样的式子为基本不等式
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
叫做正数的算术平均数
叫做正数 的几何平均数
新课讲授
上面通过考察的特殊情形获得了基本不等式。能否直接利用不等式的性质推导出基本不等式呢?下面我们来分析一下。
新课讲授
要证:①
只要证:②
要证②,只要证: ③
要证③,只要证:④
要证④,只要证:
显然,⑤成立,当且仅当a=b时,⑤中的等号成立。
只要把上述过程倒过来,就能直接推出基本不等式了。
如图,可证 因而由于小于或等于圆的半径,用不等式表示为.
显然,当且仅当点与圆心重合,即当时,上述不等式的等号成立.
基本不等式的几何意义
例1.已知x,y都是正数,求证:
(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值
探究一 对基本不等式的理解
例1.已知x,y都是正数,求证:
(2)如果和x+y等于定值S,那么当x=y时,积xy有最大值
探究一 对基本不等式的理解
总结:和定积最大,积定和最小
探究二 和定积最大,积定和最小
例2 求函数 的最小值,并求出y取得最小值时x的值。
一正:符合基本不等式 成立的前提条件,a>0,b>0
二定:化不等式的一边为定值(a+b为定值或ab为定值)
三相等:必须存在“=”成立的条件
小结--基本不等式求最值问题
一正、二定、三相等!!!!!!
和定积最大,积定和最小
【例】已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
【证明】所以
(1)等于定值P时, ,所以
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,所以
,当且仅当时,上式等号成立,此时有最大值
最值定理及其应用
①当时,,,
当且仅当时,等号成立.
②当时,,
当且仅当时,等号成立.
最值定理及其应用
基本不等式
利用基本不等式求最值的条件:
一正、二定、三相等。
基本不等式
基本不等式
3.已知都是正数,求证:
(1)如果等于定值P,那么当时,有最小值
证明:所以
(1)等于定值P时, ,∴
当且仅当时,上式等号成立,此时有最小值
(2)如果等于定值S,那么当时,有最大值
(2)时, ,两边平方,
当且仅当时,上式等号成立,此时有最大值
课堂小结
通常称不等式(1)为基本不等式,其中,叫做正数a,b的算术平均数,正数a,b的几何平均数。
基本不等式表明:两个正数的算术平均数不小于它们的几何平均数。
即:
谢谢学习
Thank you for learning
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
