(计算天天练)多边形的面积(专项训练)数学五年级上册苏教版(含答案)
文档属性
| 名称 | (计算天天练)多边形的面积(专项训练)数学五年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 07:22:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
(计算天天练)多边形的面积(专项训练)数学五年级上册苏教版
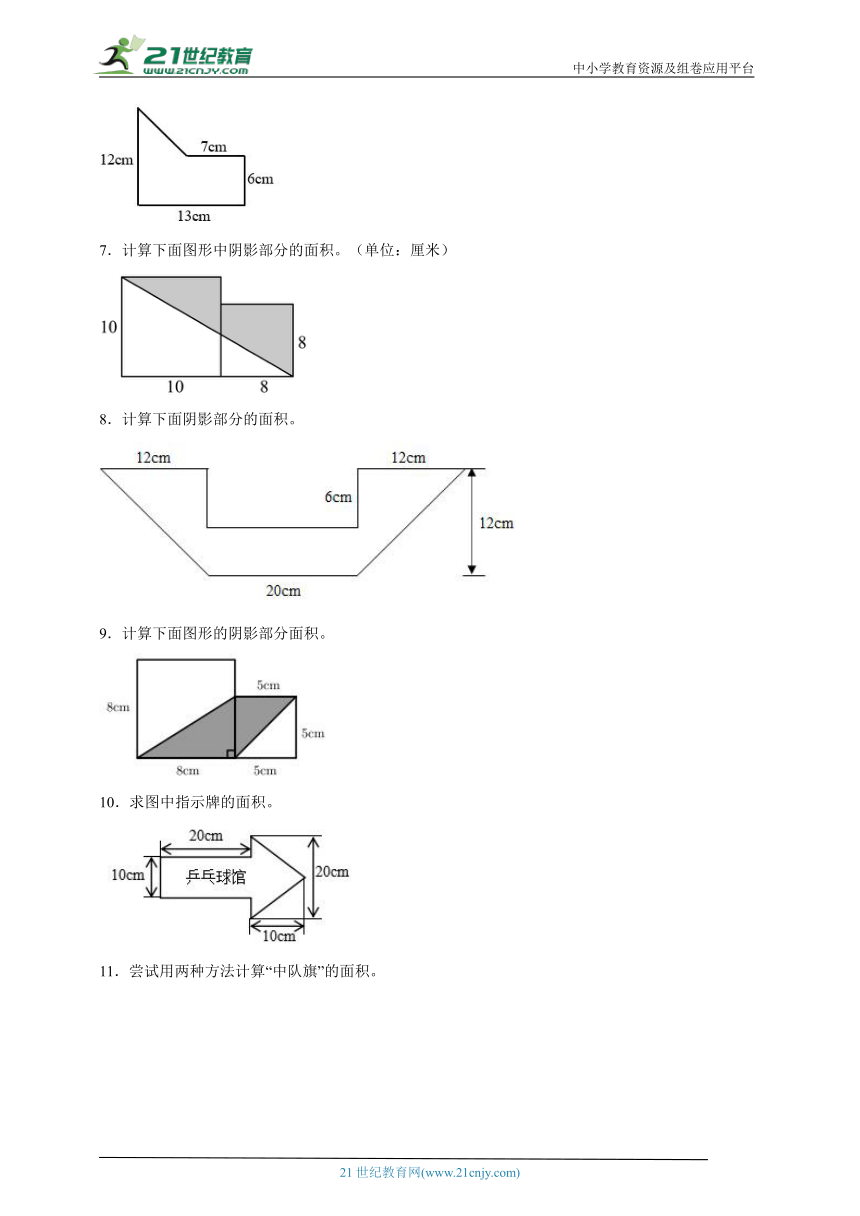
1.求下面图形的面积。
2.求下面图形的面积。
3.计算下面图形的面积。
4.计算下面图形阴影部分的面积。(单位:cm)
5.求图中阴影部分的面积.
已知正方形的周长是96cm.
6.(如图)求这个图形的面积。
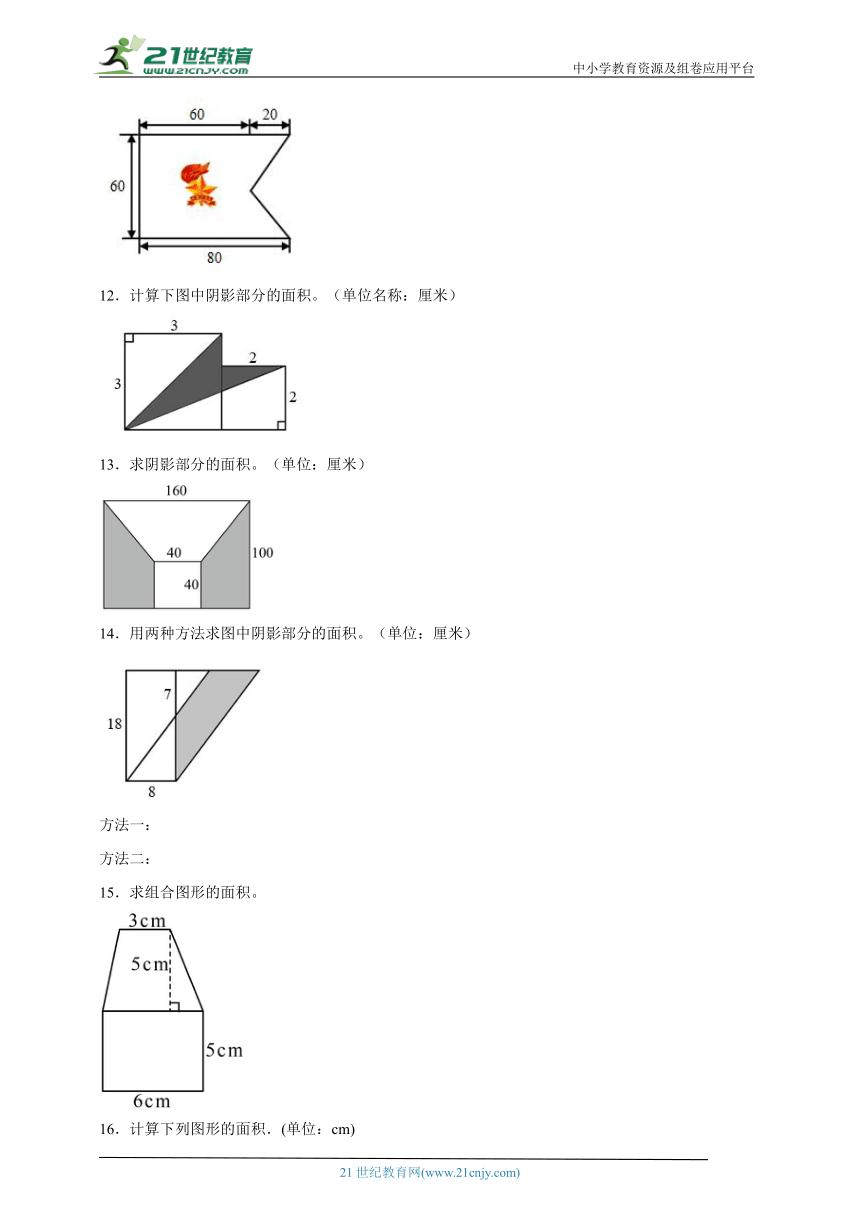
7.计算下面图形中阴影部分的面积。(单位:厘米)
8.计算下面阴影部分的面积。
9.计算下面图形的阴影部分面积。
10.求图中指示牌的面积。
11.尝试用两种方法计算“中队旗”的面积。
12.计算下图中阴影部分的面积。(单位名称:厘米)
13.求阴影部分的面积。(单位:厘米)
14.用两种方法求图中阴影部分的面积。(单位:厘米)
方法一:
方法二:
15.求组合图形的面积。
16.计算下列图形的面积.(单位:cm)
1. 2.
参考答案:
1.72
【分析】平行四边形面积=底×高,其中底和高要对应。看图,以12为底对应的高是6,以9为底对应的高是8。据此列式求出图形的面积即可。
【详解】算法一:12×6=72
算法二:9×8=72
所以,这个图形的面积是72。
2.112m2;88m2;225m2
【分析】根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,据此代入数据计算即可。
【详解】14×8=112(平方米);
16×11÷2
=176÷2
=88(平方米);
(12+18)×15÷2
=30×15÷2
=225(平方米)
3.187cm2
【分析】通过对组合图形的观察,该图形由上面的平行四边形和下面的三角形组合成,根据三角形面积公式:三角形面积=底×高÷2,平行四边形的面积公式:平行四边形面积=底×高,代入数据求解即可。
【详解】由分析可得:
平行四边形面积:17×8=136(cm2)
三角形面积:
17×6÷2
=102÷2
=51(cm2)
组合图形面积:136+51=187(cm2)
4.728cm2;22cm2
【分析】第一个图形阴影部分面积=上底是30cm,下底是52cm,高是28cm的梯形面积-底是30cm,高是28cm的三角形面积,根据梯形面积公式:(上底+下底)×高÷2,三角形面积公式:底×高÷2,代入数据,即可解答;
第二个图形阴影部分面积=边长是6cm正方形面积+边长是4cm正方形面积-底是6cm,高是(6+4)cm的三角形面积,根据正方形面积公式:边长×边长,三角形面积公式:底×高÷2,代入数据,即可解答。
【详解】(30+52)×28÷2-30×28÷2
=82×28÷2-840÷2
=2296÷2-420
=1148-420
=728(cm2)
6×6+4×4-6×(6+4)÷2
=36+16-6×10÷2
=52-60÷2
=52-30
=22(cm2)
5.504cm2
【详解】(96÷4)×(96÷4)-(96÷4-18)×(96÷4)÷2=504(cm2)
或(18+96÷4)×(96÷4)÷2=504(cm2)
6.96平方厘米
【分析】分割图形如下:
由图可知组合图形的面积=梯形的面积+长方形的面积,将数据代入梯形的面积公式S=(a+b)×h÷2,长方形的面积公式:S=ab计算即可。
【详解】
=18×6÷2+42
(平方厘米)
组合图形的面积是96平方厘米。
7.74平方厘米
【分析】根据图可知,两个正方形的面积和减去直角边为10+8=18厘米,和10厘米的直角三角形的面积即可求解。根据正方形的面积公式:边长×边长,三角形的面积公式:底×高÷2,把数代入即可求解。
【详解】10×10+8×8-(10+8)×10÷2
=100+64-18×10÷2
=164-90
=74(平方厘米)
8.264平方厘米
【分析】给原图补充一个长方形使原图成为一个梯形,则原图的面积=梯形的面积-长方形的面积,代入数据计算即可。
【详解】(12+20+12+20)×12÷2-20×6
=64×6-120
=384-120
=264(平方厘米)
9.32.5平方厘米
【分析】如下图:
阴影部分的面积=三角形1的面积+三角形2的面积,代入数据计算即可。
【详解】8×5÷2+5×5÷2
=20+12.5
=32.5(平方厘米)
10.300厘米
【分析】指示牌是由一个长20厘米,宽10厘米的长方形和一个底20厘米,高10厘米的三角形组成,根据长方形面积=长×宽和三角形面积=底×高÷2分别求出面积,再相加即可解答。
【详解】20×10+20×10÷2
=200+100
=300(厘米)
11.4200
【分析】方法一:运用分割法,将队旗分成两个梯形,然后根据梯形面积=(上底+下底)×高÷2进行解答;方法二:运用填补法,将队旗右侧填补,队旗变为长方形,然后用长方形面积减去三角形面积即可解答。
【详解】方法一:(60+80)×(60÷2)÷2×2
=140×30÷2×2
=4200÷2×2
=4200
方法二:80×60-60×20÷2
=4800-1200÷2
=4800-600
=4200
【点睛】此题主要考查学生对利用不同方法求取图形面积的应用。
12.3.5平方厘米
【分析】根据图可知,阴影部分面积=两个正方形的面积-两个空白部分三角形的面积;两个空白部分的三角形其中一个两个直角边分别是3厘米,另一个直角三角形的一条直角边是2厘米,另一条直角边是:(3+2)厘米,根据正方形的面积公式:边长×边长,三角形的面积公式:底×高÷2,把数代入公式即可求解。
【详解】3×3+2×2
=9+4
=13(平方厘米)
3×3÷2+2×(3+2)÷2
=4.5+2×5÷2
=4.5+5
=9.5(平方厘米)
13-9.5=3.5(平方厘米)
所以阴影部分面积是3.5平方厘米。
13.8400平方厘米
【分析】假设左边梯形的高为h1,右边梯形的高为h2,h1+h2=(160-40)厘米,两个梯形的上底都是40厘米,下底为100厘米,利用梯形的面积公式分别表示出左边梯形和右边梯形的面积,两个梯形的面积相加即可求出阴影部分的面积。
【详解】假设左边梯形的高为h1,右边梯形的高为h2,
h1+h2
=160-40
=120(厘米)
(40+100)×h1÷2+(40+100)×h2÷2
=140×h1÷2+140×h2÷2
=70 h1+70×h2
=70×(h1+h2)
=70×120
=8400(平方厘米)
即阴影部分的面积是8400平方厘米。
14.100平方厘米
【分析】平行四边形ABCD和长方形ABEF的面积相等,阴影部分的面积+三角形ABG的面积=梯形AGEF的面积+三角形ABG的面积,则阴影部分的面积等于梯形AGEF的面积,利用“梯形的面积=(上底+下底)×高÷2”求出阴影部分的面积;在平行四边形ABCD中,阴影部分的面积=平行四边形ABCD的面积-三角形ABG的面积,据此解答。
【详解】方法一:(7+18)×8÷2
=25×8÷2
=200÷2
=100(平方厘米)
方法二:8×18-(18-7)×8÷2
=8×18-11×8÷2
=144-44
=100(平方厘米)
所以,阴影部分的面积是100平方厘米。
15.52.5cm
【分析】组合图形的面积是梯形的面积加上长方形的面积,用梯形的面积公式:(上底+下底)×高÷2、长方形的面积公式:长×宽即可求解。
【详解】(3+6)×5÷2
=9×5÷2
=45÷2
=22.5(平方厘米)
6×5=30(平方厘米)
22.5+30=52.5(平方厘米)
16.1.30×10÷2=150(cm2)
(30+25)×20÷2=550(cm2)
150+550=700(cm2)
2.20×20=400(cm2) 20-12=8(cm)
20-14=6(cm) 8×6÷2=24(cm2)
400-24=376(cm2)
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(计算天天练)多边形的面积(专项训练)数学五年级上册苏教版
1.求下面图形的面积。
2.求下面图形的面积。
3.计算下面图形的面积。
4.计算下面图形阴影部分的面积。(单位:cm)
5.求图中阴影部分的面积.
已知正方形的周长是96cm.
6.(如图)求这个图形的面积。
7.计算下面图形中阴影部分的面积。(单位:厘米)
8.计算下面阴影部分的面积。
9.计算下面图形的阴影部分面积。
10.求图中指示牌的面积。
11.尝试用两种方法计算“中队旗”的面积。
12.计算下图中阴影部分的面积。(单位名称:厘米)
13.求阴影部分的面积。(单位:厘米)
14.用两种方法求图中阴影部分的面积。(单位:厘米)
方法一:
方法二:
15.求组合图形的面积。
16.计算下列图形的面积.(单位:cm)
1. 2.
参考答案:
1.72
【分析】平行四边形面积=底×高,其中底和高要对应。看图,以12为底对应的高是6,以9为底对应的高是8。据此列式求出图形的面积即可。
【详解】算法一:12×6=72
算法二:9×8=72
所以,这个图形的面积是72。
2.112m2;88m2;225m2
【分析】根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,据此代入数据计算即可。
【详解】14×8=112(平方米);
16×11÷2
=176÷2
=88(平方米);
(12+18)×15÷2
=30×15÷2
=225(平方米)
3.187cm2
【分析】通过对组合图形的观察,该图形由上面的平行四边形和下面的三角形组合成,根据三角形面积公式:三角形面积=底×高÷2,平行四边形的面积公式:平行四边形面积=底×高,代入数据求解即可。
【详解】由分析可得:
平行四边形面积:17×8=136(cm2)
三角形面积:
17×6÷2
=102÷2
=51(cm2)
组合图形面积:136+51=187(cm2)
4.728cm2;22cm2
【分析】第一个图形阴影部分面积=上底是30cm,下底是52cm,高是28cm的梯形面积-底是30cm,高是28cm的三角形面积,根据梯形面积公式:(上底+下底)×高÷2,三角形面积公式:底×高÷2,代入数据,即可解答;
第二个图形阴影部分面积=边长是6cm正方形面积+边长是4cm正方形面积-底是6cm,高是(6+4)cm的三角形面积,根据正方形面积公式:边长×边长,三角形面积公式:底×高÷2,代入数据,即可解答。
【详解】(30+52)×28÷2-30×28÷2
=82×28÷2-840÷2
=2296÷2-420
=1148-420
=728(cm2)
6×6+4×4-6×(6+4)÷2
=36+16-6×10÷2
=52-60÷2
=52-30
=22(cm2)
5.504cm2
【详解】(96÷4)×(96÷4)-(96÷4-18)×(96÷4)÷2=504(cm2)
或(18+96÷4)×(96÷4)÷2=504(cm2)
6.96平方厘米
【分析】分割图形如下:
由图可知组合图形的面积=梯形的面积+长方形的面积,将数据代入梯形的面积公式S=(a+b)×h÷2,长方形的面积公式:S=ab计算即可。
【详解】
=18×6÷2+42
(平方厘米)
组合图形的面积是96平方厘米。
7.74平方厘米
【分析】根据图可知,两个正方形的面积和减去直角边为10+8=18厘米,和10厘米的直角三角形的面积即可求解。根据正方形的面积公式:边长×边长,三角形的面积公式:底×高÷2,把数代入即可求解。
【详解】10×10+8×8-(10+8)×10÷2
=100+64-18×10÷2
=164-90
=74(平方厘米)
8.264平方厘米
【分析】给原图补充一个长方形使原图成为一个梯形,则原图的面积=梯形的面积-长方形的面积,代入数据计算即可。
【详解】(12+20+12+20)×12÷2-20×6
=64×6-120
=384-120
=264(平方厘米)
9.32.5平方厘米
【分析】如下图:
阴影部分的面积=三角形1的面积+三角形2的面积,代入数据计算即可。
【详解】8×5÷2+5×5÷2
=20+12.5
=32.5(平方厘米)
10.300厘米
【分析】指示牌是由一个长20厘米,宽10厘米的长方形和一个底20厘米,高10厘米的三角形组成,根据长方形面积=长×宽和三角形面积=底×高÷2分别求出面积,再相加即可解答。
【详解】20×10+20×10÷2
=200+100
=300(厘米)
11.4200
【分析】方法一:运用分割法,将队旗分成两个梯形,然后根据梯形面积=(上底+下底)×高÷2进行解答;方法二:运用填补法,将队旗右侧填补,队旗变为长方形,然后用长方形面积减去三角形面积即可解答。
【详解】方法一:(60+80)×(60÷2)÷2×2
=140×30÷2×2
=4200÷2×2
=4200
方法二:80×60-60×20÷2
=4800-1200÷2
=4800-600
=4200
【点睛】此题主要考查学生对利用不同方法求取图形面积的应用。
12.3.5平方厘米
【分析】根据图可知,阴影部分面积=两个正方形的面积-两个空白部分三角形的面积;两个空白部分的三角形其中一个两个直角边分别是3厘米,另一个直角三角形的一条直角边是2厘米,另一条直角边是:(3+2)厘米,根据正方形的面积公式:边长×边长,三角形的面积公式:底×高÷2,把数代入公式即可求解。
【详解】3×3+2×2
=9+4
=13(平方厘米)
3×3÷2+2×(3+2)÷2
=4.5+2×5÷2
=4.5+5
=9.5(平方厘米)
13-9.5=3.5(平方厘米)
所以阴影部分面积是3.5平方厘米。
13.8400平方厘米
【分析】假设左边梯形的高为h1,右边梯形的高为h2,h1+h2=(160-40)厘米,两个梯形的上底都是40厘米,下底为100厘米,利用梯形的面积公式分别表示出左边梯形和右边梯形的面积,两个梯形的面积相加即可求出阴影部分的面积。
【详解】假设左边梯形的高为h1,右边梯形的高为h2,
h1+h2
=160-40
=120(厘米)
(40+100)×h1÷2+(40+100)×h2÷2
=140×h1÷2+140×h2÷2
=70 h1+70×h2
=70×(h1+h2)
=70×120
=8400(平方厘米)
即阴影部分的面积是8400平方厘米。
14.100平方厘米
【分析】平行四边形ABCD和长方形ABEF的面积相等,阴影部分的面积+三角形ABG的面积=梯形AGEF的面积+三角形ABG的面积,则阴影部分的面积等于梯形AGEF的面积,利用“梯形的面积=(上底+下底)×高÷2”求出阴影部分的面积;在平行四边形ABCD中,阴影部分的面积=平行四边形ABCD的面积-三角形ABG的面积,据此解答。
【详解】方法一:(7+18)×8÷2
=25×8÷2
=200÷2
=100(平方厘米)
方法二:8×18-(18-7)×8÷2
=8×18-11×8÷2
=144-44
=100(平方厘米)
所以,阴影部分的面积是100平方厘米。
15.52.5cm
【分析】组合图形的面积是梯形的面积加上长方形的面积,用梯形的面积公式:(上底+下底)×高÷2、长方形的面积公式:长×宽即可求解。
【详解】(3+6)×5÷2
=9×5÷2
=45÷2
=22.5(平方厘米)
6×5=30(平方厘米)
22.5+30=52.5(平方厘米)
16.1.30×10÷2=150(cm2)
(30+25)×20÷2=550(cm2)
150+550=700(cm2)
2.20×20=400(cm2) 20-12=8(cm)
20-14=6(cm) 8×6÷2=24(cm2)
400-24=376(cm2)
【详解】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
