24.3锐角三角函数同步练习(无答案) 华东师大版九年级数学上册
文档属性
| 名称 | 24.3锐角三角函数同步练习(无答案) 华东师大版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 526.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 15:37:45 | ||
图片预览

文档简介
解直角三角形—锐角三角函数
锐角三角函数及其应用是数学中考中比较重要的考点,其考察内容主要包括①正弦、余弦、正切三函数、②特殊角的三角函数值、③解直角三角形与其应用等。而且,因为锐角三角函数的性质的特点,出题时除了会单独出题以外,还常和四边形、圆、网格图形等结合考察。本节就锐角三角函数计算及特殊角的三角函数值进行学习
第一部分 基础知识梳理
【锐角三角函数的相关概念】
在中,,,,,
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 cos (∠A为锐角)
正切 (∠A为锐角)
若,则正弦值随角度增大而增大;余弦值随角度增大而减小;正切值随角度增大而增大。
注意:正弦、余弦、正切是在一个直角三角形中引入的,实际上是两条边的比,它们是正实数,没单位,其大小只与角的大小有关,而与所在直角三角形无关。
【特殊角的三角函数】
1
第二部分 题型分类及巩固练习
【题型1 紧扣定义求三角函数值】
1、在△ABC中,∠C=90°,,则( )
A.cosA= B.sinB= C.tanA= D.tanB=
2、如图,BD⊥AC于D,CE⊥AB于E,BD与CE相交于O,则图中线段的比不能表示sinA的式子为( )
A. B. C. D.
3、如图,已知Rt△ABC中,∠ACB=90°,AC:AB=3:5,则tanA的值为( )
A. B. C. D.
4、如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于的是( )
A. B. C. D.
5、已知Rt△ABC中,∠C=90°,AC=4,BC=6,那么下列各式中,正确的是( )
A. B. C. D.tanB
6、如图,在Rt△ABC中,,,,则的值为( )
A. B. C. D.
7、如图,△ACB中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
A.a (cosα﹣cosβ). B. C.acosα D.a cosα﹣asinα a tanβ
8、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,下列结论正确的是( )
A.b=a sinA B.b=a tanA C.c=a sinA D.a=c cosB
9、Rt△ABC在中,若ABAC,则cosB= .
10、如图,在Rt△ABC中,∠C=90°,BC=12,tanA,则sinB= .
11、如图,在中,,,,点是延长线上的一点,且,则的值为
12、如图,在矩形中,,点E在上,将矩形沿折叠,点恰好落在边上的点处,则的值为 _____.
13、在Rt△ABC中,∠C=90°,cosB,求tanA的值.
14、如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.
15、如图,在Rt△ABC中, ,为上一点,交于,若AE=5,AD=4,求的值.
【题型2 构造直角三角形求锐角的三角函数值】
1、在锐角三角形ABC中,若tanA=3,那么cosA的值为( )
A. B. C. D.
2、如图,A,B,C,D均为网格图中的格点,线段AB与CD相交于点P,则∠APD的正切值为( )
A.3 B.2 C.2 D.
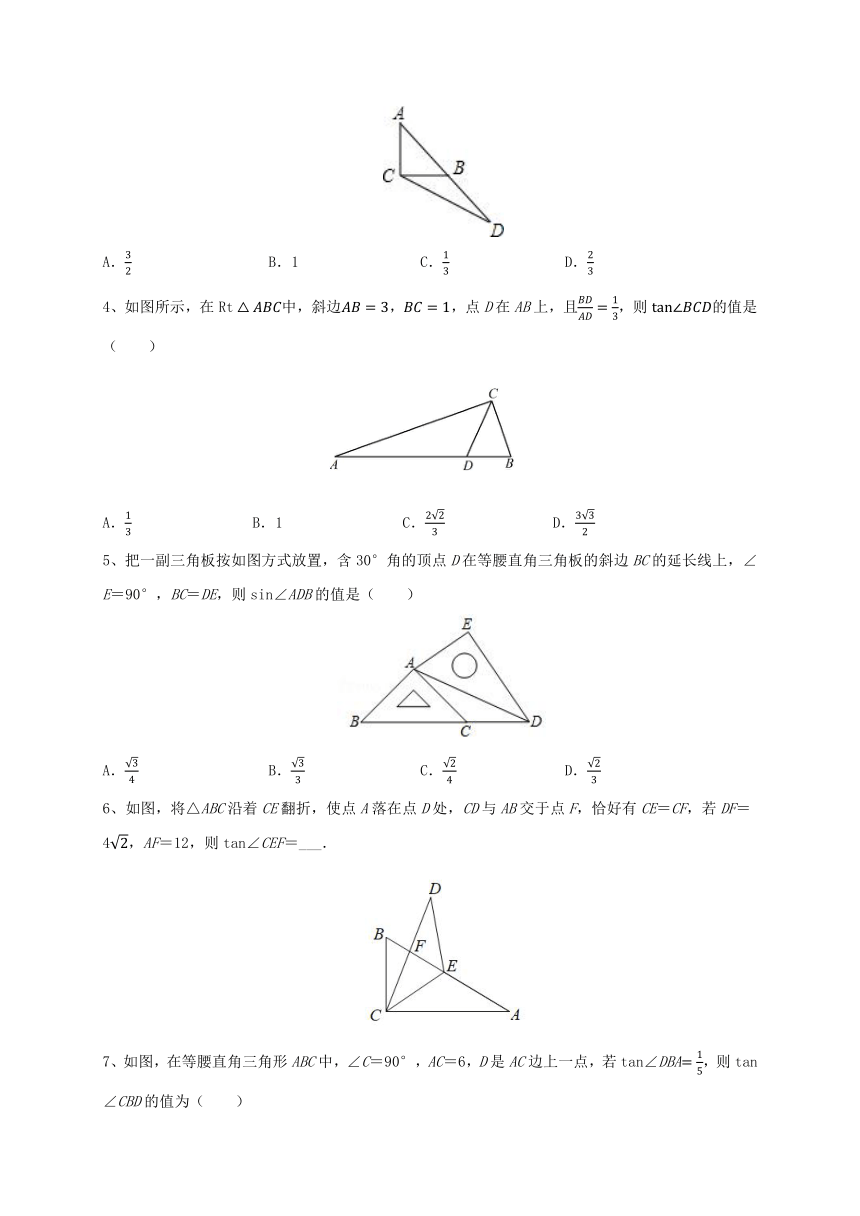
3、如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD,则tanA=( )
A. B.1 C. D.
4、如图所示,在中,斜边,,点D在AB上,且,则的值是( )
A. B.1 C. D.
5、把一副三角板按如图方式放置,含30°角的顶点D在等腰直角三角板的斜边BC的延长线上,∠E=90°,BC=DE,则sin∠ADB的值是( )
A. B. C. D.
6、如图,将△ABC沿着CE翻折,使点A落在点D处,CD与AB交于点F,恰好有CE=CF,若DF=4,AF=12,则tan∠CEF=___.
7、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA,则tan∠CBD的值为( )
A. B. C.1 D.
8、如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 _____.
9、如图,AC,BD为四边形ABCD的对角线,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC.则tan∠DBC的值是
【题型3 根据锐角的三角函数值求边长】
1、如图,大同南站某自动扶梯的倾斜角为,自动扶梯的长为15米,则大厅两层之间的高度为( )
A.米 B.米 C.米 D.以上都不对
2、在中,,,,则的长为( )
A.6 B.2 C.3 D.9
3、在中,,,,则边 的长是( )
A.3 B. C. D.
4、如图,架在消防车上的云梯AB长为15m,,,云梯底部离地面的距离BC为2m.则云梯的顶端离地面的距离AE的长为( )
A. B. C. D.
5、在Rt△ABC中,,如果,,那么等于( )
A. B. C. D.
6、如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
7、如下图所示,在矩形中,于点,设,且,,则的长为
8、如图,在中,,,点是上一点,连接.若,,则的长为
9、如图,在中,.点在内部,,且,若,,则的长为______.
10、如图,中,,点为边中点,过点作的垂线交于点,在直线上截取,使,连接、、.
(1)求证:四边形是菱形;
(2)若,,连接,求的长.
【题型4 网格中的锐角三角函数值计算】
1、如图,△ABC的顶点都在方格纸的格点上,则sinC为( )
A. B. C. D.
2、如图,点A、B、C在正方形网格的格点上,sin∠BAC=( )
A. B. C. D.
3、在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
4、如图,△ABC的顶点都在正方形网格纸的格点上,则sin .
5、由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=
6、如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则的正切值是______.
【题型5 利用增减性判断三角函数的取值范围】
1、三角函数sin30°、cos16°、cos43°之间的大小关系是( )
A.cos43°>cos16°>sin30° B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30° D.cos43°>sin30°>cos16°
2、已知是锐角三角形,若,则( )
A. B. C. D.
3、如果,那么与的差( )
A.大于0 B.小于0 C.等于0 D.不能确定
4、已知为锐角,且,则的取值范围是( )
A. B. C. D.
5、已知,A,B均为锐角,则A的取值范围是( )
A. B. C. D.
6、若是锐角,且,则( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
7、如图,梯子地面的夹角为,关于的三角函数值与梯子的倾斜程度之间的关系,下列叙述正确的是( )
A.的值越小,梯子越陡 B.的值越小,梯子越陡
C.梯子的长度决定倾斜程度 D.梯子倾斜程度与的函数值无关
8、当A为锐角,且<cosA<时,∠A的范围是( )
A.30°<∠A<45° B.60°<∠A<90° C.30°<∠A<60° D.0°<∠A<30°
9、若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60°
10已知∠A为锐角,且cosA=0.6,那么( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
11、比较大小:___________(填“”或“”或“=”).
12、比较大小:sin70°,cos70°,tan70°的大小关系是 (用 “”连接).
【题型6 利用特殊角求三角函数值】
1、在△ABC中,∠C,∠B为锐角,且满足|sinC|+(cosB)2=0,则∠A的度数为( )
A.100° B.105° C.90° D.60°
2、若菱形的周长为,高为2,则菱形两邻角的度数比为( )
A.6:1 B.5:1 C.4:1 D.3:1
3、已知在中,、都是锐角,,则的度数是( )
A. B. C. D.
4、若(tanA﹣3)2+|2cosB|=0,则△ABC的形状是( )
A.直角三角形 B.等边三角形 C.含有60°的任意三角形 D.等腰直角三角形
5、若,则锐角______°.
6、计算:______.
7、在中,若,,则__________度.
8、若,那么△ABC的形状是 等边三角形 .
9、计算:
(1)cos245°tan245°﹣tan260°.
(2).
(3).
(4).
(5).
锐角三角函数及其应用是数学中考中比较重要的考点,其考察内容主要包括①正弦、余弦、正切三函数、②特殊角的三角函数值、③解直角三角形与其应用等。而且,因为锐角三角函数的性质的特点,出题时除了会单独出题以外,还常和四边形、圆、网格图形等结合考察。本节就锐角三角函数计算及特殊角的三角函数值进行学习
第一部分 基础知识梳理
【锐角三角函数的相关概念】
在中,,,,,
定 义 表达式 取值范围 关 系
正弦 (∠A为锐角)
余弦 cos (∠A为锐角)
正切 (∠A为锐角)
若,则正弦值随角度增大而增大;余弦值随角度增大而减小;正切值随角度增大而增大。
注意:正弦、余弦、正切是在一个直角三角形中引入的,实际上是两条边的比,它们是正实数,没单位,其大小只与角的大小有关,而与所在直角三角形无关。
【特殊角的三角函数】
1
第二部分 题型分类及巩固练习
【题型1 紧扣定义求三角函数值】
1、在△ABC中,∠C=90°,,则( )
A.cosA= B.sinB= C.tanA= D.tanB=
2、如图,BD⊥AC于D,CE⊥AB于E,BD与CE相交于O,则图中线段的比不能表示sinA的式子为( )
A. B. C. D.
3、如图,已知Rt△ABC中,∠ACB=90°,AC:AB=3:5,则tanA的值为( )
A. B. C. D.
4、如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于的是( )
A. B. C. D.
5、已知Rt△ABC中,∠C=90°,AC=4,BC=6,那么下列各式中,正确的是( )
A. B. C. D.tanB
6、如图,在Rt△ABC中,,,,则的值为( )
A. B. C. D.
7、如图,△ACB中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
A.a (cosα﹣cosβ). B. C.acosα D.a cosα﹣asinα a tanβ
8、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,下列结论正确的是( )
A.b=a sinA B.b=a tanA C.c=a sinA D.a=c cosB
9、Rt△ABC在中,若ABAC,则cosB= .
10、如图,在Rt△ABC中,∠C=90°,BC=12,tanA,则sinB= .
11、如图,在中,,,,点是延长线上的一点,且,则的值为
12、如图,在矩形中,,点E在上,将矩形沿折叠,点恰好落在边上的点处,则的值为 _____.
13、在Rt△ABC中,∠C=90°,cosB,求tanA的值.
14、如图,在正方形ABCD中,M是AD的中点,BE=3AE,试求sin∠ECM的值.
15、如图,在Rt△ABC中, ,为上一点,交于,若AE=5,AD=4,求的值.
【题型2 构造直角三角形求锐角的三角函数值】
1、在锐角三角形ABC中,若tanA=3,那么cosA的值为( )
A. B. C. D.
2、如图,A,B,C,D均为网格图中的格点,线段AB与CD相交于点P,则∠APD的正切值为( )
A.3 B.2 C.2 D.
3、如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD,则tanA=( )
A. B.1 C. D.
4、如图所示,在中,斜边,,点D在AB上,且,则的值是( )
A. B.1 C. D.
5、把一副三角板按如图方式放置,含30°角的顶点D在等腰直角三角板的斜边BC的延长线上,∠E=90°,BC=DE,则sin∠ADB的值是( )
A. B. C. D.
6、如图,将△ABC沿着CE翻折,使点A落在点D处,CD与AB交于点F,恰好有CE=CF,若DF=4,AF=12,则tan∠CEF=___.
7、如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC边上一点,若tan∠DBA,则tan∠CBD的值为( )
A. B. C.1 D.
8、如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为 _____.
9、如图,AC,BD为四边形ABCD的对角线,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC.则tan∠DBC的值是
【题型3 根据锐角的三角函数值求边长】
1、如图,大同南站某自动扶梯的倾斜角为,自动扶梯的长为15米,则大厅两层之间的高度为( )
A.米 B.米 C.米 D.以上都不对
2、在中,,,,则的长为( )
A.6 B.2 C.3 D.9
3、在中,,,,则边 的长是( )
A.3 B. C. D.
4、如图,架在消防车上的云梯AB长为15m,,,云梯底部离地面的距离BC为2m.则云梯的顶端离地面的距离AE的长为( )
A. B. C. D.
5、在Rt△ABC中,,如果,,那么等于( )
A. B. C. D.
6、如图,等腰Rt△ABC中,∠A=90°,AB=AC,BD为△ABC的角平分线,若,则的长为( )
A.3 B. C.4 D.
7、如下图所示,在矩形中,于点,设,且,,则的长为
8、如图,在中,,,点是上一点,连接.若,,则的长为
9、如图,在中,.点在内部,,且,若,,则的长为______.
10、如图,中,,点为边中点,过点作的垂线交于点,在直线上截取,使,连接、、.
(1)求证:四边形是菱形;
(2)若,,连接,求的长.
【题型4 网格中的锐角三角函数值计算】
1、如图,△ABC的顶点都在方格纸的格点上,则sinC为( )
A. B. C. D.
2、如图,点A、B、C在正方形网格的格点上,sin∠BAC=( )
A. B. C. D.
3、在如图所示8×8的网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点E,则∠AED的正切值是( )
A.2 B. C. D.
4、如图,△ABC的顶点都在正方形网格纸的格点上,则sin .
5、由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=
6、如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则的正切值是______.
【题型5 利用增减性判断三角函数的取值范围】
1、三角函数sin30°、cos16°、cos43°之间的大小关系是( )
A.cos43°>cos16°>sin30° B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30° D.cos43°>sin30°>cos16°
2、已知是锐角三角形,若,则( )
A. B. C. D.
3、如果,那么与的差( )
A.大于0 B.小于0 C.等于0 D.不能确定
4、已知为锐角,且,则的取值范围是( )
A. B. C. D.
5、已知,A,B均为锐角,则A的取值范围是( )
A. B. C. D.
6、若是锐角,且,则( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
7、如图,梯子地面的夹角为,关于的三角函数值与梯子的倾斜程度之间的关系,下列叙述正确的是( )
A.的值越小,梯子越陡 B.的值越小,梯子越陡
C.梯子的长度决定倾斜程度 D.梯子倾斜程度与的函数值无关
8、当A为锐角,且<cosA<时,∠A的范围是( )
A.30°<∠A<45° B.60°<∠A<90° C.30°<∠A<60° D.0°<∠A<30°
9、若锐角α满足cosα<且tanα<,则α的范围是( )
A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60°
10已知∠A为锐角,且cosA=0.6,那么( )
A.0°<∠A<30° B.30°<∠A<45° C.45°<∠A<60° D.60°<∠A<90°
11、比较大小:___________(填“”或“”或“=”).
12、比较大小:sin70°,cos70°,tan70°的大小关系是 (用 “”连接).
【题型6 利用特殊角求三角函数值】
1、在△ABC中,∠C,∠B为锐角,且满足|sinC|+(cosB)2=0,则∠A的度数为( )
A.100° B.105° C.90° D.60°
2、若菱形的周长为,高为2,则菱形两邻角的度数比为( )
A.6:1 B.5:1 C.4:1 D.3:1
3、已知在中,、都是锐角,,则的度数是( )
A. B. C. D.
4、若(tanA﹣3)2+|2cosB|=0,则△ABC的形状是( )
A.直角三角形 B.等边三角形 C.含有60°的任意三角形 D.等腰直角三角形
5、若,则锐角______°.
6、计算:______.
7、在中,若,,则__________度.
8、若,那么△ABC的形状是 等边三角形 .
9、计算:
(1)cos245°tan245°﹣tan260°.
(2).
(3).
(4).
(5).
