苏教版六年级数学上册第1课《分数除以整数》课件(共28张PPT)
文档属性
| 名称 | 苏教版六年级数学上册第1课《分数除以整数》课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-09 22:29:47 | ||
图片预览







文档简介
(共28张PPT)
分数除以整数
苏教版数学六年级上册
运算中的推理
杯里有4升果汁,平均分给2个小朋友喝,每人可以喝多少升?
有
所
现
发
4÷2
2
1
4×
=
16÷3
3
1
16×
a÷b
(b不等于0)
=
=
b
1
a×
提
出
想
猜
÷2
5
4
5
4
×
2
1
2
1
?
5
2
=
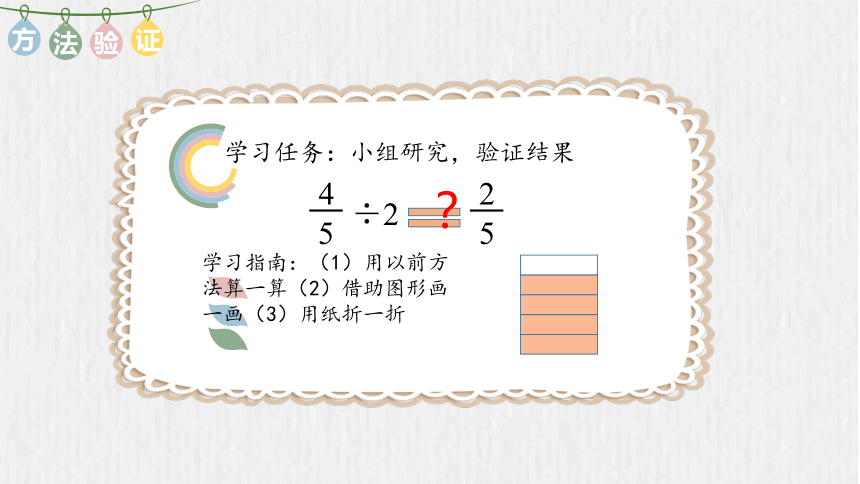
学习任务:小组研究,验证结果
学习指南:(1)用以前方法算一算(2)借助图形画一画(3)用纸折一折
方
法
证
验
÷2
5
4
5
2
?
方
法
证
验
÷2
5
4
=0.8÷2=0.4
分数转化为小数
算一算:
商不变的规律
÷2
5
4
=( )÷( )=
5
4
2
1
×
2
1
×
2
5
2
方
法
证
验
画一画:
÷2
5
4
5
4÷2
=
5
2
=
把4个 平均分成2份
5
1
方
法
证
验
折一折:
每份是 的
5
4
2
1
÷2
5
4
5
4
×
2
1
=
=
5
2
方
法
证
验
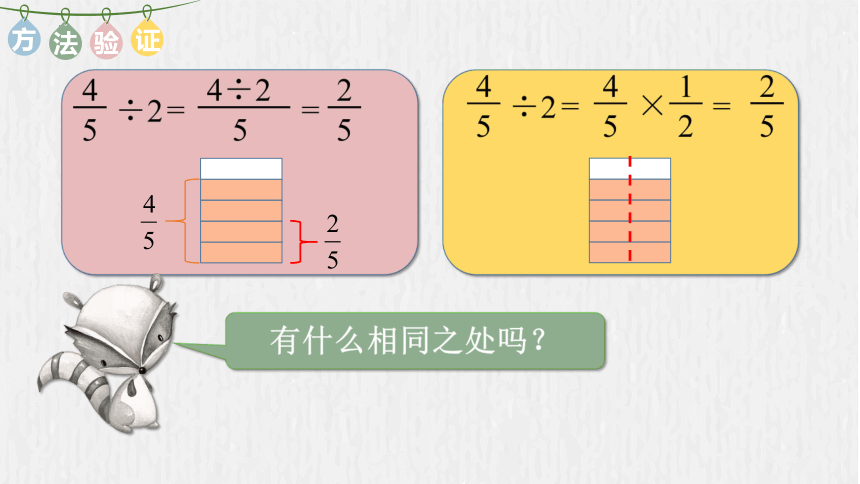
÷2
5
4
5
4
×
2
1
=
=
5
2
÷2
5
4
5
4÷2
=
5
2
=
有什么相同之处吗?
方
法
证
验
4÷2
2
1
4×
=
16÷3
3
1
16×
=
a÷b
(b不等于0)
=
b
1
a×
÷2
5
4
5
4
×
2
1
=
÷3
5
4
5
4
×
3
1
?
÷2
5
4
5
4
×
2
1
=
÷3
5
4
5
4
×
3
1
=
÷4
5
4
5
4
×
4
1
=
÷5
5
4
5
4
×
5
1
=
÷c
a
b
a
b
×
c
1
=
(c不等于0)
分数除以整数,等于分数乘这个整数的倒数。
得
出
论
结
巩
固
习
练
1. 先在下图中涂色表示 ,再按除法算式分一分,并填空。
1
3
÷3=( )
7
6
÷3就是求 的 是多少。
7
6
( )
( )
2.计算下面各题的结果。
÷4
8
5
÷3
7
6
÷20
16
15
÷6
13
9
8
5
×
4
1
=
7
6
×
3
1
=
16
15
×
20
1
=
13
9
×
6
1
=
=
32
5
=
7
2
=
64
3
=
26
3
巩
固
习
练
3.芳芳将 米的丝带剪成同样长的8段,每段丝带有多长?每份占了全长的几分之几?
5
4
÷8
5
4
5
4
×
8
1
=
=
10
1
(米)
1÷8=
8
1
答:每段丝带有 ,每份占了全长的 。
10
1
米
8
1
巩
固
习
练
整数除法
商不变规律
小数除法
分数除法
画图
乘法
商不变的规律
转化
谢 谢 !
《分数除以整数》
教学阐释
教学分析
教学目标
说重点与难点
说教学思考
1
2
3
说课提纲
CONTENTS
说教学过程
4
5
教材中例1主要教学分数除以整数。教材结合分果汁的问题情景,较好地利用数形结合的方法来解决分数除以整数的算理。教材主要分两个层次编排:先解决分数的分子能被整数整除的情况;再引出分子不能被整数整除的情况。旨在启发学生通过思考总结出分数除以整数一般的计算方法。在教学时,学生经过“图——数——式”的活动对算理理解透彻,自然而然便能思考得出:分数除以整数(0除外)等于分数乘以这个整数的倒数,这一结论的得出,为后面的分数除以分数奠定良好的基础。
1
教材分析
1
学情分析
“分数除以整数”是在学生掌握整数除法、分数乘法和倒数的基础上进行教学的。本学段的学生,在观察能力、记忆能力、想象能力、抽象能力、逻辑思维能力等学习能力上有了很大程度的发展和提升,同时也具有一定的问题意识、与他人合作的意识。在探究的过程中能多角度思考问题,能通过动手、动脑,发现其中的数学问题、提出数学问题并能够分析解决问题,还可以对自己的发现进行清晰的表述,能较好地表达自己的观点,阐述自己的思维过程,并且在教师的引导下或借助图示的直观性,有一定的知识系统化整合的能力,优化解题方法的能力。所以根据学生的情况,在已有知识上,通过探究、图示进行引导式教学,让学生探究发现并理解分数除法的算理和优化计算的方法。
使学生体会分数除以整数的意义,理解并掌握分数除以整数的计算方法,能正确计算分数除以整数。
1
2
教学目标
PPT下载 http:///xiazai/
2
3
使学生经历探索分数除以整数计算方法的过程,感悟运算的一致性,发展运算能力和推理意识,体会转化的数学思想。
使学生主动参与学习活动,养成自主探索、合作交流的习惯;增强学习数学的积极性,体会学习成功的乐趣。
分数除法意义的理解。
教学重点
3
教学重难点
分数除以整数算法的探究和算理的理解。
教学难点
分数除以整数算法的探究。
教学重点
1.如何让学生感悟分数除法与整数除法运算的一致性?
2.如何利用相关概念推理分数除法“颠倒”相乘的运算法则?
4
教学思考
5
教学过程
1
3
2
知识迁移,凸显运算意义
数形结合,理解计算方法
对比优化,内化计算法则
4
巩固练习,完善认知结构
《课标》内容要求指出“感悟运算的一致性”,教学提示也明确指出“数的运算教学应注重对整数、小数和分数四则运算的统筹,让学生进一步感悟运算的一致性”。分数除法与整数除法的逻辑推理规则是一致的,因此教学时,通过问题情境,让学生从整数除法的意义“平均分”出发,列出算式、理解算式并计算结果,发现规律。用这一规律让学生在整数除法与分数除法之间建立初步联系,为推理分数除法的法则奠定基础。这样的教学,不是就计算讲计算,而是将计算学习的横纵联系、思维脉络清晰地展现,这对学生来说,既是数学活动经验的积累,又是学习能力、方法的渗透,更是不可小觑的数学素养的提升。
知识迁移,凸显运算意义
5
教学过程
数形结合,理解计算方法
5
教学过程
《课标》的内容要求和学业要求都强调学生“运算能力和推理意识”的形成与提升。教学时通过问题情境引导学生用不同的方法验证出 ÷2与 × 的相等关系。在探究的过程中,学生尝试从除法意义、分数单位、分数与除法间的关系,分数的基本性质、商不变的规律等方面入手,将未知转化成已知,用已知解决未知,学生经历了观察、操作、归纳等探究活动,感悟分数除法的本质仍是整数除法,体会运算的一致性。同时,将分数除法问题转化成分数乘法,根据分数乘法意义“求一个数的几分之几是多少”,用 × 也可以解决这个问题,让学生在分数除法与分数乘法之间建立初步联系,为进一步推理分数除法的运算法则提供理论支撑。
对比优化,内化计算法则
5
教学过程
÷2是分数除以整数的特殊情况,计算时可以类比分数乘整数的方法,直接用4÷2的商2作分子,分母不变。而当学生经历了算法多样化,并且对于运算的道理有所理解后,,如果不及时沟通几种算法之间的联系,草率地牵引到通法上来,是不符合学生认知规律的。出于这这两方面的考虑,对比优化,在教学时便显得格外重要。在这一过程中学生依据除法的意义,运用分数乘法与整数乘法的联系进行自主推理,一步步地理解为什么在进行分数除以整数的计算时需要将除法转化成乘法。这样,不仅可以帮助学生理解分数除法的算理,也为学生推理意识的形成提供了充足的空间。
巩固练习,完善认知结构
5
教学过程
在练习的设计中,注重练习的层次性,以题组的形式设计了针对性的练习,既有“分子是除数倍数”这样的特例,也有“分子不是除数倍数”的一般分数除法。第3题是一道非常典型的题,它考查学生对于每份的数量与分率的区分,会有相当一部分的人,不能区分“每份量”与“分率”,在刚学完分数除以整数求“每份量”进行进一步区分,有助于学生对两种题型的理解。
感谢您的耐心聆听
分数除以整数
苏教版数学六年级上册
运算中的推理
杯里有4升果汁,平均分给2个小朋友喝,每人可以喝多少升?
有
所
现
发
4÷2
2
1
4×
=
16÷3
3
1
16×
a÷b
(b不等于0)
=
=
b
1
a×
提
出
想
猜
÷2
5
4
5
4
×
2
1
2
1
?
5
2
=
学习任务:小组研究,验证结果
学习指南:(1)用以前方法算一算(2)借助图形画一画(3)用纸折一折
方
法
证
验
÷2
5
4
5
2
?
方
法
证
验
÷2
5
4
=0.8÷2=0.4
分数转化为小数
算一算:
商不变的规律
÷2
5
4
=( )÷( )=
5
4
2
1
×
2
1
×
2
5
2
方
法
证
验
画一画:
÷2
5
4
5
4÷2
=
5
2
=
把4个 平均分成2份
5
1
方
法
证
验
折一折:
每份是 的
5
4
2
1
÷2
5
4
5
4
×
2
1
=
=
5
2
方
法
证
验
÷2
5
4
5
4
×
2
1
=
=
5
2
÷2
5
4
5
4÷2
=
5
2
=
有什么相同之处吗?
方
法
证
验
4÷2
2
1
4×
=
16÷3
3
1
16×
=
a÷b
(b不等于0)
=
b
1
a×
÷2
5
4
5
4
×
2
1
=
÷3
5
4
5
4
×
3
1
?
÷2
5
4
5
4
×
2
1
=
÷3
5
4
5
4
×
3
1
=
÷4
5
4
5
4
×
4
1
=
÷5
5
4
5
4
×
5
1
=
÷c
a
b
a
b
×
c
1
=
(c不等于0)
分数除以整数,等于分数乘这个整数的倒数。
得
出
论
结
巩
固
习
练
1. 先在下图中涂色表示 ,再按除法算式分一分,并填空。
1
3
÷3=( )
7
6
÷3就是求 的 是多少。
7
6
( )
( )
2.计算下面各题的结果。
÷4
8
5
÷3
7
6
÷20
16
15
÷6
13
9
8
5
×
4
1
=
7
6
×
3
1
=
16
15
×
20
1
=
13
9
×
6
1
=
=
32
5
=
7
2
=
64
3
=
26
3
巩
固
习
练
3.芳芳将 米的丝带剪成同样长的8段,每段丝带有多长?每份占了全长的几分之几?
5
4
÷8
5
4
5
4
×
8
1
=
=
10
1
(米)
1÷8=
8
1
答:每段丝带有 ,每份占了全长的 。
10
1
米
8
1
巩
固
习
练
整数除法
商不变规律
小数除法
分数除法
画图
乘法
商不变的规律
转化
谢 谢 !
《分数除以整数》
教学阐释
教学分析
教学目标
说重点与难点
说教学思考
1
2
3
说课提纲
CONTENTS
说教学过程
4
5
教材中例1主要教学分数除以整数。教材结合分果汁的问题情景,较好地利用数形结合的方法来解决分数除以整数的算理。教材主要分两个层次编排:先解决分数的分子能被整数整除的情况;再引出分子不能被整数整除的情况。旨在启发学生通过思考总结出分数除以整数一般的计算方法。在教学时,学生经过“图——数——式”的活动对算理理解透彻,自然而然便能思考得出:分数除以整数(0除外)等于分数乘以这个整数的倒数,这一结论的得出,为后面的分数除以分数奠定良好的基础。
1
教材分析
1
学情分析
“分数除以整数”是在学生掌握整数除法、分数乘法和倒数的基础上进行教学的。本学段的学生,在观察能力、记忆能力、想象能力、抽象能力、逻辑思维能力等学习能力上有了很大程度的发展和提升,同时也具有一定的问题意识、与他人合作的意识。在探究的过程中能多角度思考问题,能通过动手、动脑,发现其中的数学问题、提出数学问题并能够分析解决问题,还可以对自己的发现进行清晰的表述,能较好地表达自己的观点,阐述自己的思维过程,并且在教师的引导下或借助图示的直观性,有一定的知识系统化整合的能力,优化解题方法的能力。所以根据学生的情况,在已有知识上,通过探究、图示进行引导式教学,让学生探究发现并理解分数除法的算理和优化计算的方法。
使学生体会分数除以整数的意义,理解并掌握分数除以整数的计算方法,能正确计算分数除以整数。
1
2
教学目标
PPT下载 http:///xiazai/
2
3
使学生经历探索分数除以整数计算方法的过程,感悟运算的一致性,发展运算能力和推理意识,体会转化的数学思想。
使学生主动参与学习活动,养成自主探索、合作交流的习惯;增强学习数学的积极性,体会学习成功的乐趣。
分数除法意义的理解。
教学重点
3
教学重难点
分数除以整数算法的探究和算理的理解。
教学难点
分数除以整数算法的探究。
教学重点
1.如何让学生感悟分数除法与整数除法运算的一致性?
2.如何利用相关概念推理分数除法“颠倒”相乘的运算法则?
4
教学思考
5
教学过程
1
3
2
知识迁移,凸显运算意义
数形结合,理解计算方法
对比优化,内化计算法则
4
巩固练习,完善认知结构
《课标》内容要求指出“感悟运算的一致性”,教学提示也明确指出“数的运算教学应注重对整数、小数和分数四则运算的统筹,让学生进一步感悟运算的一致性”。分数除法与整数除法的逻辑推理规则是一致的,因此教学时,通过问题情境,让学生从整数除法的意义“平均分”出发,列出算式、理解算式并计算结果,发现规律。用这一规律让学生在整数除法与分数除法之间建立初步联系,为推理分数除法的法则奠定基础。这样的教学,不是就计算讲计算,而是将计算学习的横纵联系、思维脉络清晰地展现,这对学生来说,既是数学活动经验的积累,又是学习能力、方法的渗透,更是不可小觑的数学素养的提升。
知识迁移,凸显运算意义
5
教学过程
数形结合,理解计算方法
5
教学过程
《课标》的内容要求和学业要求都强调学生“运算能力和推理意识”的形成与提升。教学时通过问题情境引导学生用不同的方法验证出 ÷2与 × 的相等关系。在探究的过程中,学生尝试从除法意义、分数单位、分数与除法间的关系,分数的基本性质、商不变的规律等方面入手,将未知转化成已知,用已知解决未知,学生经历了观察、操作、归纳等探究活动,感悟分数除法的本质仍是整数除法,体会运算的一致性。同时,将分数除法问题转化成分数乘法,根据分数乘法意义“求一个数的几分之几是多少”,用 × 也可以解决这个问题,让学生在分数除法与分数乘法之间建立初步联系,为进一步推理分数除法的运算法则提供理论支撑。
对比优化,内化计算法则
5
教学过程
÷2是分数除以整数的特殊情况,计算时可以类比分数乘整数的方法,直接用4÷2的商2作分子,分母不变。而当学生经历了算法多样化,并且对于运算的道理有所理解后,,如果不及时沟通几种算法之间的联系,草率地牵引到通法上来,是不符合学生认知规律的。出于这这两方面的考虑,对比优化,在教学时便显得格外重要。在这一过程中学生依据除法的意义,运用分数乘法与整数乘法的联系进行自主推理,一步步地理解为什么在进行分数除以整数的计算时需要将除法转化成乘法。这样,不仅可以帮助学生理解分数除法的算理,也为学生推理意识的形成提供了充足的空间。
巩固练习,完善认知结构
5
教学过程
在练习的设计中,注重练习的层次性,以题组的形式设计了针对性的练习,既有“分子是除数倍数”这样的特例,也有“分子不是除数倍数”的一般分数除法。第3题是一道非常典型的题,它考查学生对于每份的数量与分率的区分,会有相当一部分的人,不能区分“每份量”与“分率”,在刚学完分数除以整数求“每份量”进行进一步区分,有助于学生对两种题型的理解。
感谢您的耐心聆听
