人教版六年级下册数学图形的认识——立体图形课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下册数学图形的认识——立体图形课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
立体图形
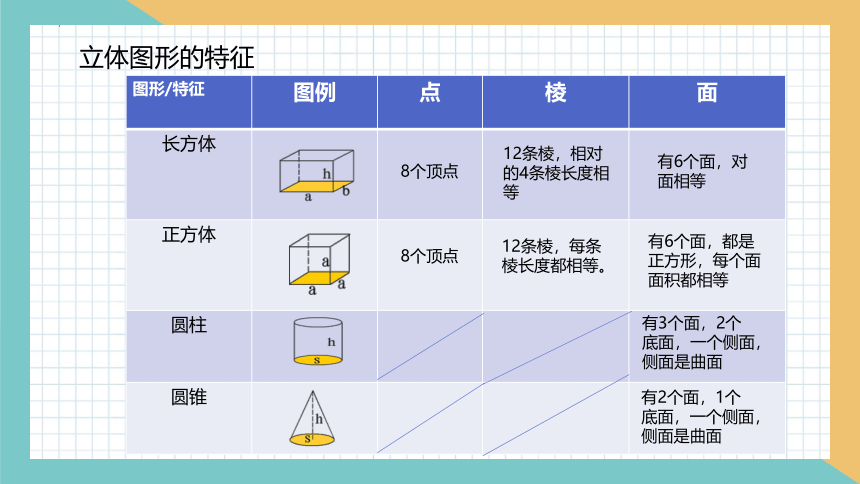
立体图形的特征
图形/特征 图例 点 棱 面
长方体
正方体
圆柱
圆锥
8个顶点
8个顶点
12条棱,相对的4条棱长度相等
12条棱,每条棱长度都相等。
有6个面,对面相等
有6个面,都是正方形,每个面面积都相等
有3个面,2个底面,一个侧面,侧面是曲面
有2个面,1个底面,一个侧面,侧面是曲面
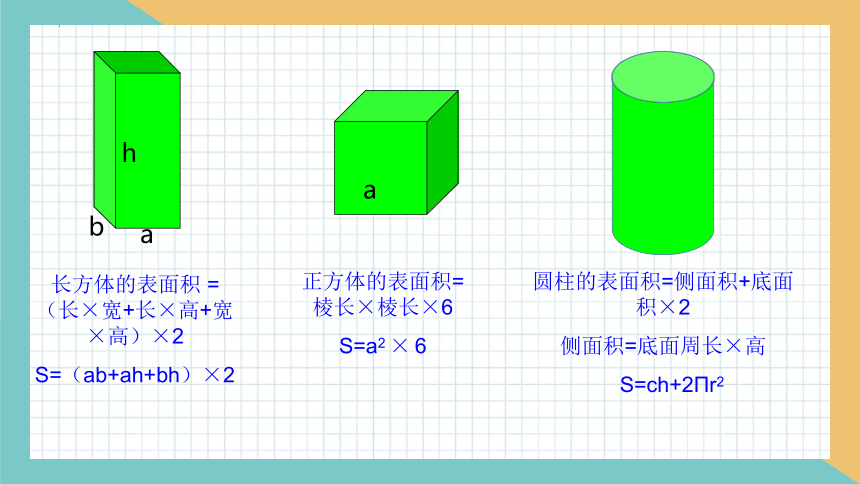
长方体的表面积 =(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
a
b
h
正方体的表面积= 棱长×棱长×6
S=a2 × 6
a
圆柱的表面积=侧面积+底面积×2
侧面积=底面周长×高
S=ch+2Πr2
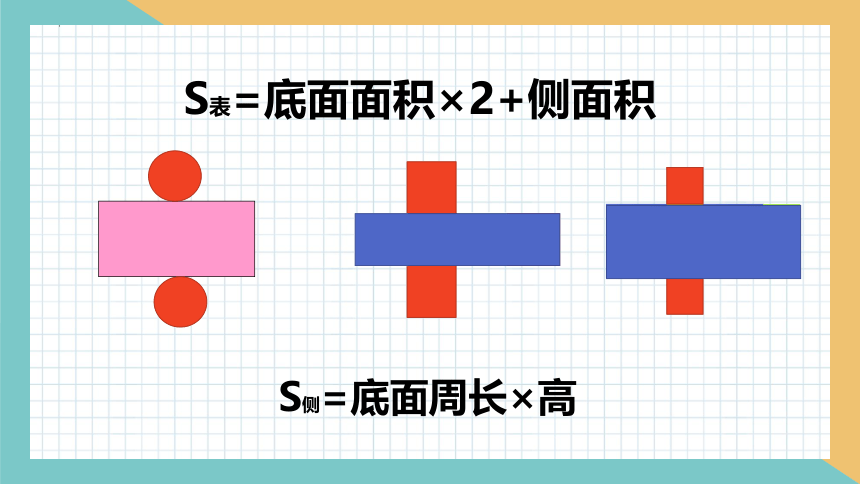
S表=底面面积×2+侧面积
S侧=底面周长×高
立体图形的体积是指什么?
物体所占空间的大小
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
h
a
b
a
a
a
s
h
s
h
动画
柱体
练一 练
(1)做一个圆柱形的油箱
需要多少平方分米的铁皮?
(2)做一个圆柱形的水桶
(无盖),需要多少平方分米的铁皮?
(3)做一节圆柱形的通风管,需要多少平方分米的铁皮?
连一连
求一个侧面
求一个侧面加两个底面
求一个侧面加一个底面
一个游泳池长50米,宽25米,池深2米,游泳池里的水深1.8米。
(1)求这个泳池的占地面积,是求( ),列式为
(2)在游泳池的底面和四周都铺上一层瓷砖,需要多少平方米的瓷砖,是求( ),列式为
(3)游泳池里有多少水,是求( ),列式为
50×25×1.8
50×25
50×25+2×(50×2+25×2)
填空
底面积
一个底面积+一个侧面积
水的体积
50米
25米
2
米
对比练习
下面是两位同学对同一圆柱的两种不同的切法(平均分成两块)。甲乙切分后,甲的表面积比原来增加( )平方厘米,乙的表面积比原来增加了( )平方厘米。
甲
乙
r=5cm
h=10cm
157
200
圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?
25.12÷4÷3.14÷2
(1)求底面半径:
=6.28÷3.14÷2
=1(cm)
(1)求原来的圆柱体积:
3.14×12×10
=31.4(cm3)
答:原来圆柱的体积是31.4cm3。
拓展提升
1、一个底面半径是6cm,高是4cm的圆柱形容器中装满了水,现在把水倒入一个底面半径为6cm的圆锥形容器中刚好装满。圆锥形容器的高是多少厘米?
圆柱的体积;6×6×3.14×4=452.16(立方厘米)
等积问题
圆锥的高:452.16×3÷(6×6×3.14)=12(厘米)
V柱=V锥
sh=3sh
3h=h
3×4=12(厘米)
答:圆锥形容器的高是3厘米。
1
1、一个圆锥形沙堆,底面周长是12.56米,高12米,将这堆沙子铺在10米宽的路上铺2厘米厚,能铺多少米?
半径:12.56÷3.14÷2=2(米)
圆锥的体积:2×2×3.14×12÷3=50.24(立方米)
长方体的长:50.24÷10÷0.02=251.2(米)
答:能铺251.2米长。
解决问题
2、一个底面内半径是12cm的圆柱形杯中装有水,水里浸没一个底面直径是12cm,高是18cm的圆锥形铁块,当铁块从中取出时,杯中水面会下降多少厘米?
圆锥的体积:(12÷2)2×3.14×18÷3=678.24(立方厘米)
圆柱的高:678.24÷(122×3.14)=1.5(厘米)
答:会下降1.5厘米。
3、一个圆柱形玻璃容器,从里面量,底面直径是40cm,容器中水面离容器口2cm,将一个高为15cm的圆锥形铁块完全没入水中,水会溢出40ml。圆锥形铁块的底面积是多少平方厘米?
(40÷2)2×3.14×2=2512(立方厘米)
40ml=40cm3
2512+40=2552(立方厘米)
2552×3÷15=510.4(平方厘米)
答:圆锥形铁块的底面积是510.4平方厘米
课堂小结
立体图形
立体图形的特征
图形/特征 图例 点 棱 面
长方体
正方体
圆柱
圆锥
8个顶点
8个顶点
12条棱,相对的4条棱长度相等
12条棱,每条棱长度都相等。
有6个面,对面相等
有6个面,都是正方形,每个面面积都相等
有3个面,2个底面,一个侧面,侧面是曲面
有2个面,1个底面,一个侧面,侧面是曲面
长方体的表面积 =(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
a
b
h
正方体的表面积= 棱长×棱长×6
S=a2 × 6
a
圆柱的表面积=侧面积+底面积×2
侧面积=底面周长×高
S=ch+2Πr2
S表=底面面积×2+侧面积
S侧=底面周长×高
立体图形的体积是指什么?
物体所占空间的大小
V=
V=
V=
V=
abh
a
3
sh
1
3
sh
V = sh
h
a
b
a
a
a
s
h
s
h
动画
柱体
练一 练
(1)做一个圆柱形的油箱
需要多少平方分米的铁皮?
(2)做一个圆柱形的水桶
(无盖),需要多少平方分米的铁皮?
(3)做一节圆柱形的通风管,需要多少平方分米的铁皮?
连一连
求一个侧面
求一个侧面加两个底面
求一个侧面加一个底面
一个游泳池长50米,宽25米,池深2米,游泳池里的水深1.8米。
(1)求这个泳池的占地面积,是求( ),列式为
(2)在游泳池的底面和四周都铺上一层瓷砖,需要多少平方米的瓷砖,是求( ),列式为
(3)游泳池里有多少水,是求( ),列式为
50×25×1.8
50×25
50×25+2×(50×2+25×2)
填空
底面积
一个底面积+一个侧面积
水的体积
50米
25米
2
米
对比练习
下面是两位同学对同一圆柱的两种不同的切法(平均分成两块)。甲乙切分后,甲的表面积比原来增加( )平方厘米,乙的表面积比原来增加了( )平方厘米。
甲
乙
r=5cm
h=10cm
157
200
圆柱长10厘米,接上4厘米的一段后,表面积增加了25.12平方厘米,求原来圆柱的体积是多少立方厘米?
25.12÷4÷3.14÷2
(1)求底面半径:
=6.28÷3.14÷2
=1(cm)
(1)求原来的圆柱体积:
3.14×12×10
=31.4(cm3)
答:原来圆柱的体积是31.4cm3。
拓展提升
1、一个底面半径是6cm,高是4cm的圆柱形容器中装满了水,现在把水倒入一个底面半径为6cm的圆锥形容器中刚好装满。圆锥形容器的高是多少厘米?
圆柱的体积;6×6×3.14×4=452.16(立方厘米)
等积问题
圆锥的高:452.16×3÷(6×6×3.14)=12(厘米)
V柱=V锥
sh=3sh
3h=h
3×4=12(厘米)
答:圆锥形容器的高是3厘米。
1
1、一个圆锥形沙堆,底面周长是12.56米,高12米,将这堆沙子铺在10米宽的路上铺2厘米厚,能铺多少米?
半径:12.56÷3.14÷2=2(米)
圆锥的体积:2×2×3.14×12÷3=50.24(立方米)
长方体的长:50.24÷10÷0.02=251.2(米)
答:能铺251.2米长。
解决问题
2、一个底面内半径是12cm的圆柱形杯中装有水,水里浸没一个底面直径是12cm,高是18cm的圆锥形铁块,当铁块从中取出时,杯中水面会下降多少厘米?
圆锥的体积:(12÷2)2×3.14×18÷3=678.24(立方厘米)
圆柱的高:678.24÷(122×3.14)=1.5(厘米)
答:会下降1.5厘米。
3、一个圆柱形玻璃容器,从里面量,底面直径是40cm,容器中水面离容器口2cm,将一个高为15cm的圆锥形铁块完全没入水中,水会溢出40ml。圆锥形铁块的底面积是多少平方厘米?
(40÷2)2×3.14×2=2512(立方厘米)
40ml=40cm3
2512+40=2552(立方厘米)
2552×3÷15=510.4(平方厘米)
答:圆锥形铁块的底面积是510.4平方厘米
课堂小结
