5.4 平行线的性质定理和判定定理 教案 (表格式) 青岛版数学八年级上册
文档属性
| 名称 | 5.4 平行线的性质定理和判定定理 教案 (表格式) 青岛版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-10 00:00:00 | ||
图片预览


文档简介
年级科目 八年级数学 课题 5.4 平行线的性质定理和判定定理
教学 目标 1、掌握证明题的一般步骤,正确写出已知、求证、证明过程。 2、了解两个互逆命题的条件和结论之间的关系。
重点 难点 正确写出一个命题的逆命题 掌握几何证明已知、求证、证明的过程。
教 学 过 程
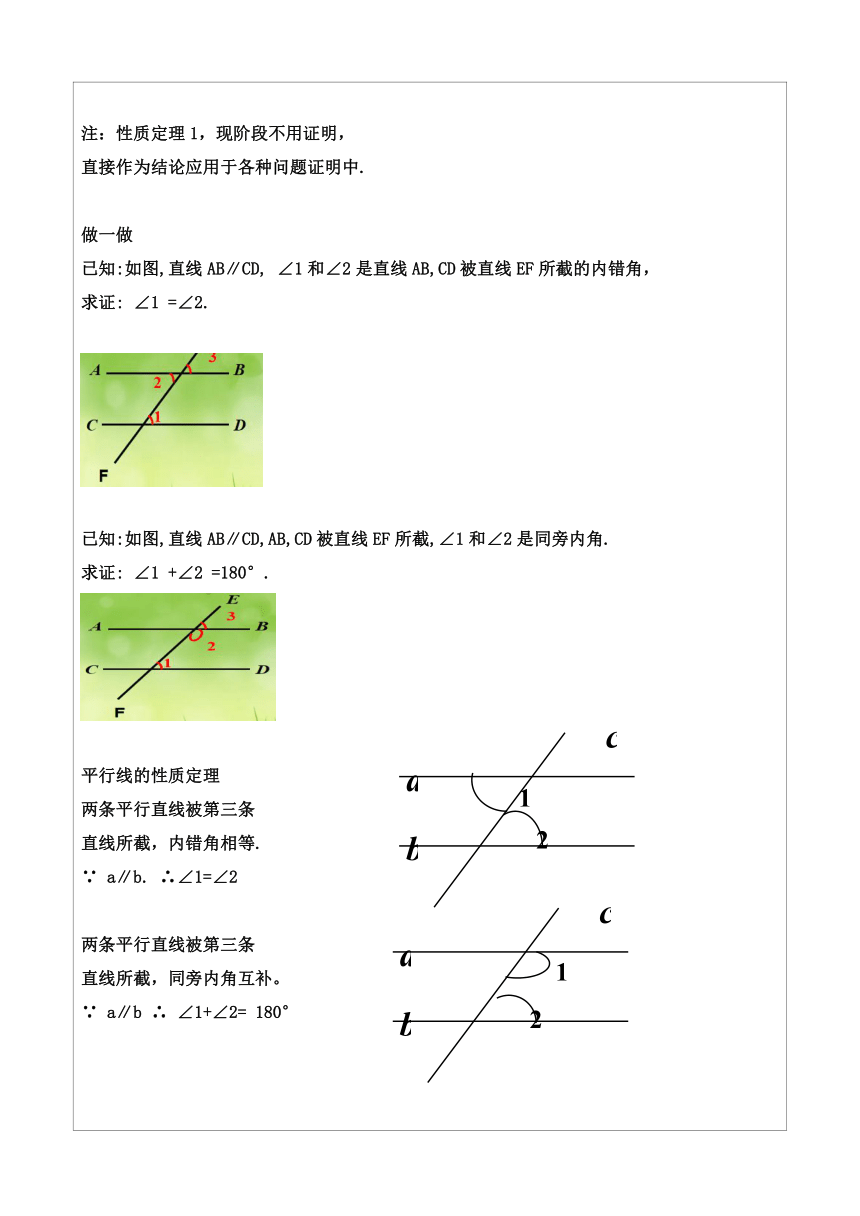
温馨提示 1.请同学们打开课本第166页,准备好笔、练习本; 2.端正坐姿、精神饱满,准备上课. 温故知新 平行线的性质定理: 1、两条平行直线被第三条直线所截,同位角相等. 2、两条平行直线被第三条直线所截,内错角相等. 3、两条平行直线被第三条直线所截,同旁内角互补。 平行线的性质定理1 两条平行直线被第三条直线所截, 同位角相等. (
a
b
c
2
1
) ∵ a∥b ∴ ∠1=∠2 注:性质定理1,现阶段不用证明, 直接作为结论应用于各种问题证明中. 做一做 已知:如图,直线AB∥CD, ∠1和∠2是直线AB,CD被直线EF所截的内错角, 求证: ∠1 =∠2. 已知:如图,直线AB∥CD,AB,CD被直线EF所截,∠1和∠2是同旁内角. 求证: ∠1 +∠2 =180°. (
a
b
c
1
2
) 平行线的性质定理 两条平行直线被第三条 直线所截,内错角相等. (
a
b
c
1
2
)∵ a∥b. ∴∠1=∠2 两条平行直线被第三条 直线所截,同旁内角互补。 ∵ a∥b ∴ ∠1+∠2= 180° 比一比 已知:如图,a∥b,c∥d, ∠1=73°. 求∠2和∠3的度数. 解:∵a ∥b(已知) ∴∠2=∠1(两直线平行, 内错角相等) ∵∠1=73° (已知) ∴∠2=73°(等量代换) ∵c ∥d(已知) ∴∠2+∠3=180°(两直线平行,同旁内角互补) ∴∠3=180°-∠ 2 (等式的性质) ∴∠3=180°-73 °=107 °(等量代换) (
c
d
a
b
1
2
3
) 平行线的判定定理 1、两条直线被第三条直线所截,如 果同位角相等,那么两直线平行。 2、两条直线被第三条直线所截,如果内错角相等,那么两直线平行。 3、两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 ∵ ∠1=∠2, ∴ a∥b. 注:作为基本事实,直接作为结论应用于 各种问题证明中. 平行线的判定定理 判定定理2: 两条直线被第三条直线所截如果内错角相等,那么两直线平行 ∵ ∠1=∠2, ∴ a∥b. 判定定理3: 两条直线被第三条直线所截如果同旁内角互补,那么两直线平行. ∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 【跟踪训练】 如图:直线AB,CD都和AE相交, 且 ∠1+∠A=180°. 求证:AB//CD 证明: ∵∠1+∠A=180°( 已知 ) ∠1=∠2(对顶角相等) ∴∠2+∠A=180°(等量代换). ∴ 自学指导 请同学们用3分钟的时间,高效自学课本 第167页交流与发现下面的内容,并完成以下任务: 1.什么是原命题、逆命题、互逆命题、 ? 2.什么是逆定理? 大家谈谈 如果两个角是直角, 那么这两个角相等. 如果两个角相等, 那么这两个角是直角. 如果两个三角形全等,那么它们的对应边相等. 如果两个三角形对应边相等,那么这两个三角形全等. 如果a,b互为相反数,那么a+b=0. 如果a+b=0,那么a,b互为相反数. 如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。 一个命题是真命题,它的逆命题不一定是真命题 如果一个定理的逆命题也是真命题,那么这个逆 命题就是原定理的逆定理。 你能说出下列命题的逆命题吗?它们的逆命题是真命题还是假命题? (1) 如果两个角相等,那么这两个角的补角相等。 (2)对顶角相等. (3)全等三角形的对应角相等。 注:先确定命题的条件和结论,然后再确定逆命题. 归纳总结、能力提升 a 1 这节课你有哪些收获?小组内交流。 b 3 当堂检测,检查效果 1、已知:如图+=180 ,求证:直线a//b. c 2、互为逆命题的两个命题的条件和结论有什么关系? 3、写出下列命题的逆命题,并分别指出它是真命题还是假命题。 (1)全等三角形的对应角相等。 (2) 所有的正方形都是相似图形。 作业:必做题课本168页1、2、3题 选做题课本169页6题 预习作业:预习5.5三角形内角和定理 教学反思:
教学 目标 1、掌握证明题的一般步骤,正确写出已知、求证、证明过程。 2、了解两个互逆命题的条件和结论之间的关系。
重点 难点 正确写出一个命题的逆命题 掌握几何证明已知、求证、证明的过程。
教 学 过 程
温馨提示 1.请同学们打开课本第166页,准备好笔、练习本; 2.端正坐姿、精神饱满,准备上课. 温故知新 平行线的性质定理: 1、两条平行直线被第三条直线所截,同位角相等. 2、两条平行直线被第三条直线所截,内错角相等. 3、两条平行直线被第三条直线所截,同旁内角互补。 平行线的性质定理1 两条平行直线被第三条直线所截, 同位角相等. (
a
b
c
2
1
) ∵ a∥b ∴ ∠1=∠2 注:性质定理1,现阶段不用证明, 直接作为结论应用于各种问题证明中. 做一做 已知:如图,直线AB∥CD, ∠1和∠2是直线AB,CD被直线EF所截的内错角, 求证: ∠1 =∠2. 已知:如图,直线AB∥CD,AB,CD被直线EF所截,∠1和∠2是同旁内角. 求证: ∠1 +∠2 =180°. (
a
b
c
1
2
) 平行线的性质定理 两条平行直线被第三条 直线所截,内错角相等. (
a
b
c
1
2
)∵ a∥b. ∴∠1=∠2 两条平行直线被第三条 直线所截,同旁内角互补。 ∵ a∥b ∴ ∠1+∠2= 180° 比一比 已知:如图,a∥b,c∥d, ∠1=73°. 求∠2和∠3的度数. 解:∵a ∥b(已知) ∴∠2=∠1(两直线平行, 内错角相等) ∵∠1=73° (已知) ∴∠2=73°(等量代换) ∵c ∥d(已知) ∴∠2+∠3=180°(两直线平行,同旁内角互补) ∴∠3=180°-∠ 2 (等式的性质) ∴∠3=180°-73 °=107 °(等量代换) (
c
d
a
b
1
2
3
) 平行线的判定定理 1、两条直线被第三条直线所截,如 果同位角相等,那么两直线平行。 2、两条直线被第三条直线所截,如果内错角相等,那么两直线平行。 3、两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行。 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 ∵ ∠1=∠2, ∴ a∥b. 注:作为基本事实,直接作为结论应用于 各种问题证明中. 平行线的判定定理 判定定理2: 两条直线被第三条直线所截如果内错角相等,那么两直线平行 ∵ ∠1=∠2, ∴ a∥b. 判定定理3: 两条直线被第三条直线所截如果同旁内角互补,那么两直线平行. ∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 【跟踪训练】 如图:直线AB,CD都和AE相交, 且 ∠1+∠A=180°. 求证:AB//CD 证明: ∵∠1+∠A=180°( 已知 ) ∠1=∠2(对顶角相等) ∴∠2+∠A=180°(等量代换). ∴ 自学指导 请同学们用3分钟的时间,高效自学课本 第167页交流与发现下面的内容,并完成以下任务: 1.什么是原命题、逆命题、互逆命题、 ? 2.什么是逆定理? 大家谈谈 如果两个角是直角, 那么这两个角相等. 如果两个角相等, 那么这两个角是直角. 如果两个三角形全等,那么它们的对应边相等. 如果两个三角形对应边相等,那么这两个三角形全等. 如果a,b互为相反数,那么a+b=0. 如果a+b=0,那么a,b互为相反数. 如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。 一个命题是真命题,它的逆命题不一定是真命题 如果一个定理的逆命题也是真命题,那么这个逆 命题就是原定理的逆定理。 你能说出下列命题的逆命题吗?它们的逆命题是真命题还是假命题? (1) 如果两个角相等,那么这两个角的补角相等。 (2)对顶角相等. (3)全等三角形的对应角相等。 注:先确定命题的条件和结论,然后再确定逆命题. 归纳总结、能力提升 a 1 这节课你有哪些收获?小组内交流。 b 3 当堂检测,检查效果 1、已知:如图+=180 ,求证:直线a//b. c 2、互为逆命题的两个命题的条件和结论有什么关系? 3、写出下列命题的逆命题,并分别指出它是真命题还是假命题。 (1)全等三角形的对应角相等。 (2) 所有的正方形都是相似图形。 作业:必做题课本168页1、2、3题 选做题课本169页6题 预习作业:预习5.5三角形内角和定理 教学反思:
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
