青岛版九年级数学下册7.3 圆柱的侧面展开图(第2课时)
文档属性
| 名称 | 青岛版九年级数学下册7.3 圆柱的侧面展开图(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 716.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览




文档简介
课件13张PPT。7.3 圆柱的侧面展开图
第2课时1.了解圆柱的侧面展开图是矩形;
2.使学生会计算圆柱的侧面积或全面积;
3.利用“转化思想”,求有关圆柱体实际问题.1.圆柱的侧面展开图为矩形;
2.一边是圆柱的母线(高),一边是圆柱底面圆的周长;
3.S圆柱侧=底面圆周长×圆柱母线
(S圆柱侧=底面周长×高).如图,一个圆柱体的底面周长为24厘米,母线AB为4厘米,BC是上底的直径.一只蚂蚁从下底面的点A处出发爬行到上底面的点C处.
(1)如果它沿圆柱体的侧面爬行,其最短路径长是多少(精确到0.1厘米)?
(2)如果将蚂蚁“沿圆柱体的侧面”改为“沿圆柱体的表面”,(1)的答案还是最短路径吗?
(3)当圆柱体底面半径r变化,而母线长h不变时,试比较沿圆柱体侧面由A处爬行到C处的最短路径与沿母线AB再沿上底
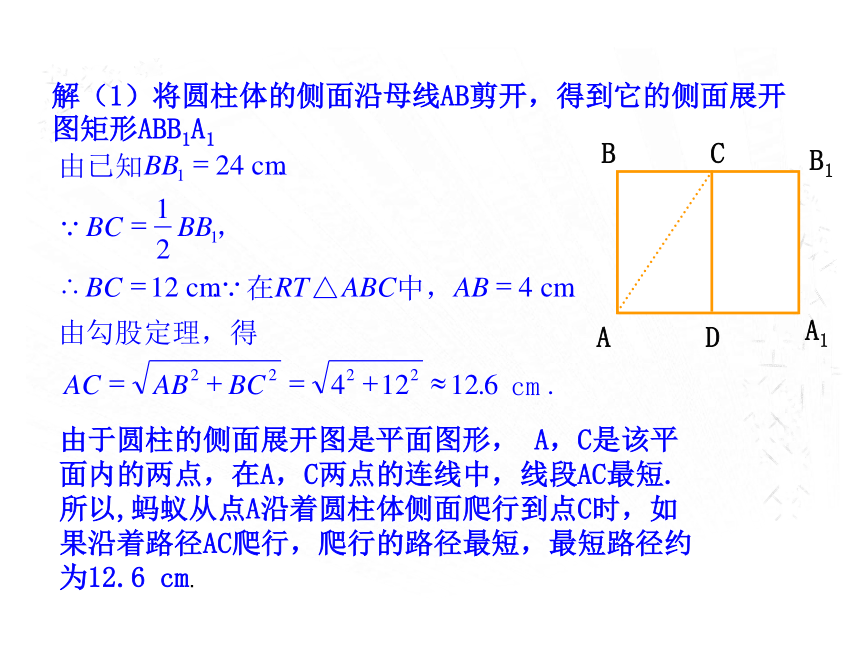
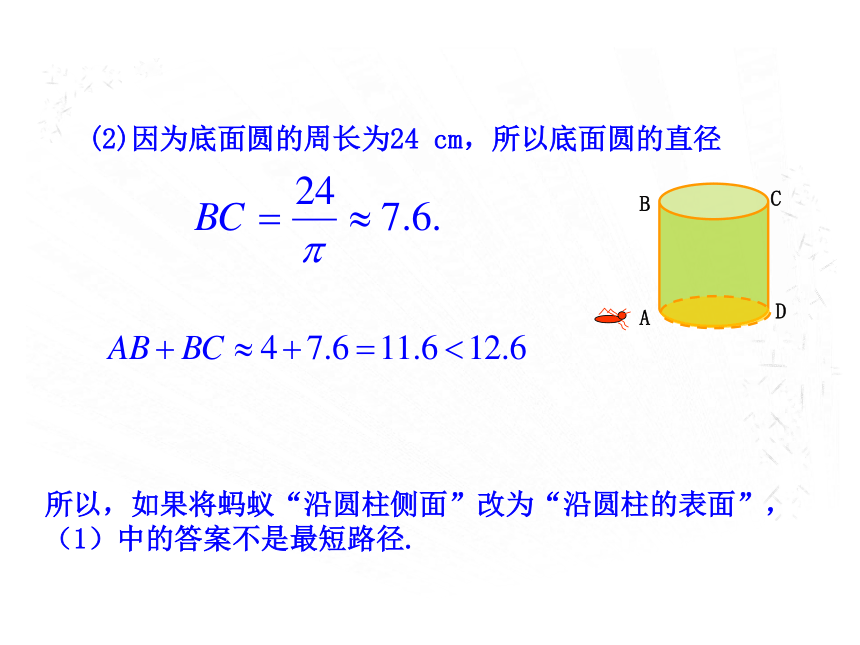
面直径BC爬行到C处的路径的长短.解(1)将圆柱体的侧面沿母线AB剪开,得到它的侧面展开图矩形ABB1A1由于圆柱的侧面展开图是平面图形, A,C是该平面内的两点,在A,C两点的连线中,线段AC最短.所以,蚂蚁从点A沿着圆柱体侧面爬行到点C时,如果沿着路径AC爬行,爬行的路径最短,最短路径约为12.6 cm.(2)因为底面圆的周长为24 cm,所以底面圆的直径所以,如果将蚂蚁“沿圆柱侧面”改为“沿圆柱的表面”,
(1)中的答案不是最短路径.(3)当圆柱体底面半径r变化,圆柱体母线长h不变时,设沿圆柱体侧面从A处到C处的最短路径长为l1,可知设路径A-B-C的长为l2. 1.有一圆形油罐底面圆的周长为24 m,高为6 m,一只蚂蚁从距底面1 m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 分析:
由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1 m处和长24 m的中点处,即AB长为最短路线.(如图)2.一个圆柱体的表面积和长方形的面积相等,长方形的长等于
圆柱体的底面周长,已知长方形的面积是251.2平方厘米,圆柱
体的底面半径是2厘米.圆柱体的高是多少厘米?解:251.2-3.14×(2+2)×2 =251.2-3.14×8 =251.2-25.12 =226.08(平方厘米) 226.08÷(3.14×2×2) =226.08÷12.56 =18(厘米) 答:圆柱体的高是18 厘米. 析:根据圆柱的底面半径是2厘米,可求圆柱的底面积,用长
方形的面积减去圆柱的2个底面积,即可得出圆柱的侧面积,
据此利用侧面积除以圆柱的底面周长,即可求出圆柱的高. 1.圆柱的形成、圆柱的概念、圆柱的性质、圆柱的侧面展开图及其面积计算.
2.思想:“转化思想”,求圆柱的侧面积(立体问题)求矩形的面积(平面问题).
3.利用“转化思想”,求有关圆柱体实际问题.
再见
第2课时1.了解圆柱的侧面展开图是矩形;
2.使学生会计算圆柱的侧面积或全面积;
3.利用“转化思想”,求有关圆柱体实际问题.1.圆柱的侧面展开图为矩形;
2.一边是圆柱的母线(高),一边是圆柱底面圆的周长;
3.S圆柱侧=底面圆周长×圆柱母线
(S圆柱侧=底面周长×高).如图,一个圆柱体的底面周长为24厘米,母线AB为4厘米,BC是上底的直径.一只蚂蚁从下底面的点A处出发爬行到上底面的点C处.
(1)如果它沿圆柱体的侧面爬行,其最短路径长是多少(精确到0.1厘米)?
(2)如果将蚂蚁“沿圆柱体的侧面”改为“沿圆柱体的表面”,(1)的答案还是最短路径吗?
(3)当圆柱体底面半径r变化,而母线长h不变时,试比较沿圆柱体侧面由A处爬行到C处的最短路径与沿母线AB再沿上底
面直径BC爬行到C处的路径的长短.解(1)将圆柱体的侧面沿母线AB剪开,得到它的侧面展开图矩形ABB1A1由于圆柱的侧面展开图是平面图形, A,C是该平面内的两点,在A,C两点的连线中,线段AC最短.所以,蚂蚁从点A沿着圆柱体侧面爬行到点C时,如果沿着路径AC爬行,爬行的路径最短,最短路径约为12.6 cm.(2)因为底面圆的周长为24 cm,所以底面圆的直径所以,如果将蚂蚁“沿圆柱侧面”改为“沿圆柱的表面”,
(1)中的答案不是最短路径.(3)当圆柱体底面半径r变化,圆柱体母线长h不变时,设沿圆柱体侧面从A处到C处的最短路径长为l1,可知设路径A-B-C的长为l2. 1.有一圆形油罐底面圆的周长为24 m,高为6 m,一只蚂蚁从距底面1 m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 分析:
由于蚂蚁是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1 m处和长24 m的中点处,即AB长为最短路线.(如图)2.一个圆柱体的表面积和长方形的面积相等,长方形的长等于
圆柱体的底面周长,已知长方形的面积是251.2平方厘米,圆柱
体的底面半径是2厘米.圆柱体的高是多少厘米?解:251.2-3.14×(2+2)×2 =251.2-3.14×8 =251.2-25.12 =226.08(平方厘米) 226.08÷(3.14×2×2) =226.08÷12.56 =18(厘米) 答:圆柱体的高是18 厘米. 析:根据圆柱的底面半径是2厘米,可求圆柱的底面积,用长
方形的面积减去圆柱的2个底面积,即可得出圆柱的侧面积,
据此利用侧面积除以圆柱的底面周长,即可求出圆柱的高. 1.圆柱的形成、圆柱的概念、圆柱的性质、圆柱的侧面展开图及其面积计算.
2.思想:“转化思想”,求圆柱的侧面积(立体问题)求矩形的面积(平面问题).
3.利用“转化思想”,求有关圆柱体实际问题.
再见
