第5章 对函数的再探索单元检测题

第5章 对函数的再探索检测题
（本检测题满分：100分，时间：90分钟）
一、选择题（每小题3分，共30分）
1.（2014·湖南娄底中考）函数中自变量的取值范围是（ ）
A． B. C． D．
2.若反比例函数y=的图象位于第二、四象限，则k的取值可能是( )
A.0 B.2 C.3 D.4
3.如图，反比例函数在第二象限的图象上有两点A、B，它们的横坐标分别为－1、－3，直线AB与x轴交于点C，则△AOC的面积为（ ）
A.8 B.10 C.12 D.24
4.把抛物线y=先向右平移1个单位长度，再向上平移2个单位长度后，所得函数的表达式为（ ）
A. B.
C. D.
5.二次函数y＝ax2＋bx－1(a≠0)的图象经过点(1，1)，则代数式1－a－b的值为（ ）
A．－3 B．－1 C．2 D．5
6.已知点A（－2，），B（－1，），C（3，）都在反比例函数的图
象上，则的大小关系是( ）
A. B.
C. D.
7.已知二次函数，当取（≠）时，函数值相等，则当取时，函数值为（　　）
A. B. C. D.c
8.已知二次函数，当取任意实数时，都有，则的取值范围是（ ）
A． B． C． D．
9.（2014·重庆中考）2014年5月 ( http: / / www.21cnjy.com )10日上午，小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿.接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一会儿，小华继续录入并加快了录入速度，直至录入完成.设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x的函数关系的大致图象是（ ）
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
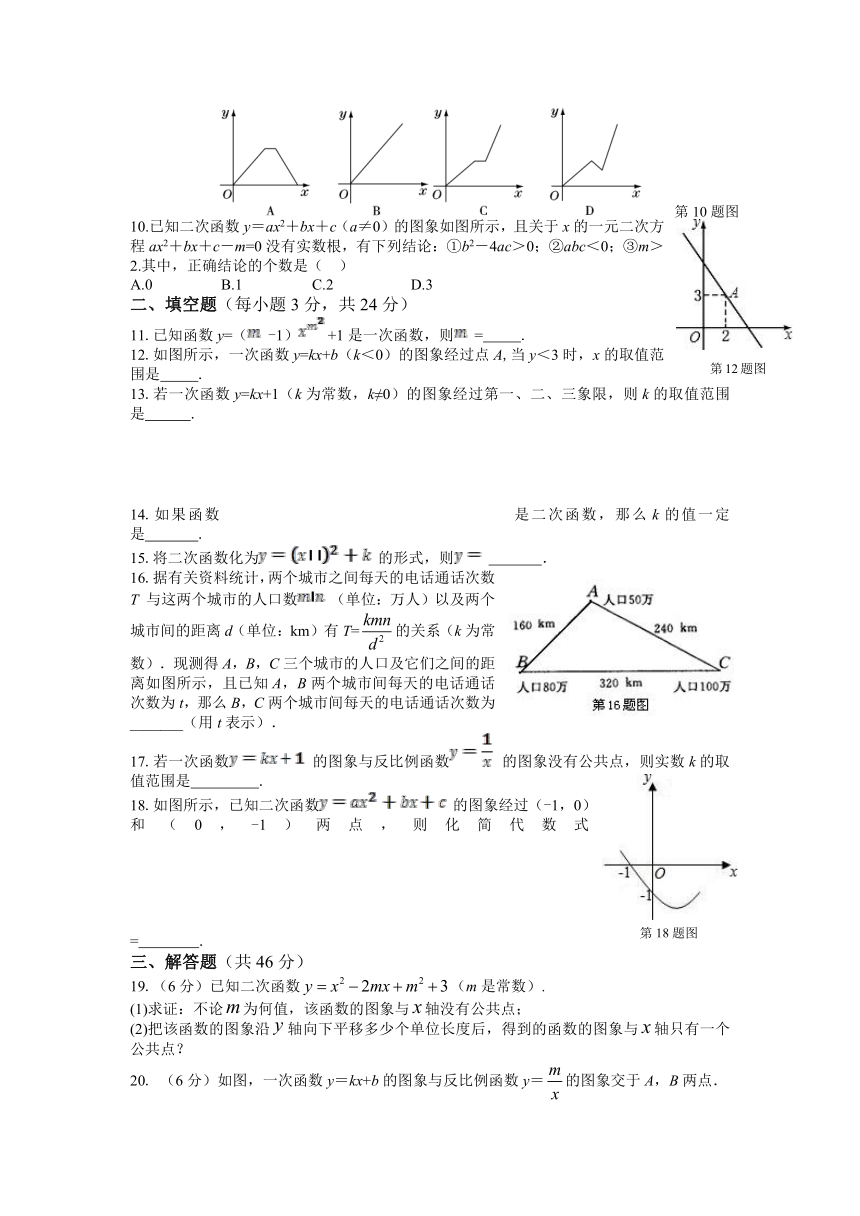
10.已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，且关于x的一元二次方程ax2＋bx＋c－m=0没有实数根，有下列结论：①b2－4ac＞0；②abc＜0；③m＞2.其中，正确结论的个数是（ ）
A.0 B.1 C.2 D.3
二、填空题（每小题3分，共24分）
11.已知函数y=（-1）+1是一次函数，则= .
12.如图所示，一次函数y=kx+b（k＜0）的图象经过点A,当y＜3时，x的取值范围是 .
13.若一次函数y=kx+1（k为常数，k≠0）的图象经过第一、二、三象限，则k的取值范围是 .
14.如果函数是二次函数，那么k的值一定是 .
15.将二次函数化为的形式，则 ．
16.据有关资料统计，两个城市之间每天的电话通话次数T与这两个城市的人口数（单位：万人）以及两个城市间的距离d（单位：km）有T=的关系（k为常数）．现测得A，B，C三个城市的人口及它们之间的距离如图所示，且已知A，B两个城市间每天的电话通话次数为t，那么B，C两个城市间每天的电话通话次数为_______（用t表示）．
17.若一次函数的图象与反比例函数 的图象没有公共点，则实数k的取值范围是 .
18.如图所示，已知二次函数的图象经过（-1，0）和（0，-1）两点，则化简代数式
= .
三、解答题（共46分）
19.（6分）已知二次函数（m是常数）.
(1)求证：不论为何值，该函数的图象与轴没有公共点；
(2)把该函数的图象沿轴向下平移多少个单位长度后，得到的函数的图象与轴只有一个公共点？
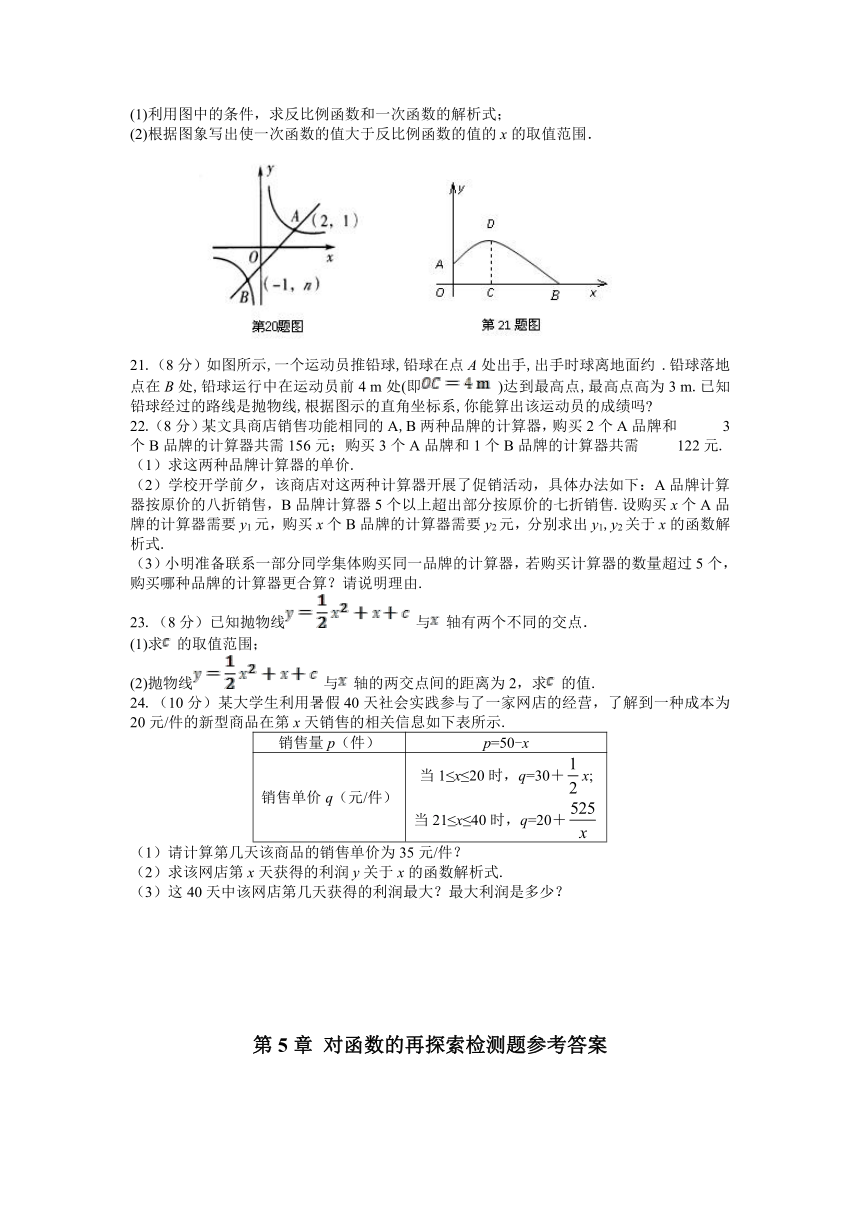
20. （6分）如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于A，B两点．
(1)利用图中的条件，求反比例函数和一次函数的解析式；
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．
21.（8分）如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约.铅球落地点在B处,铅球运行中在运动员前4 m处(即)达到最高点,最高点高为3 m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗
22.（8分）某文具商店销售功能相同的A, ( http: / / www.21cnjy.com )B两种品牌的计算器，购买2个A品牌和 3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需 122元.
（1）求这两种品牌计算器的单价.
（2）学校开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器5个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y1元，购买x个B品牌的计算器需要y2元，分别求出y1,y2关于x的函数解析式.
（3）小明准备联系一部分同学集体购买同一品牌的计算器，若购买计算器的数量超过5个，购买哪种品牌的计算器更合算？请说明理由.
23.（8分）已知抛物线与轴有两个不同的交点．
(1)求的取值范围；
(2)抛物线与轴的两交点间的距离为2，求的值.
24.（10分）某大学生利用暑假40天社会实践参与了一家网店的经营，了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p（件） p=50-x
销售单价q（元/件） 当1≤x≤20时，q=30＋x;当21≤x≤40时，q=20＋ QUOTE
（1）请计算第几天该商品的销售单价为35元/件？
（2）求该网店第x天获得的利润y关于x的函数解析式.
（3）这40天中该网店第几天获得的利润最大？最大利润是多少？
第5章 对函数的再探索检测题参考答案
1.C 解析:本题主要考查自变量的取值范围，函数关系式中含有二次根式，根据二次根式的意义即可求解.由题意，得，解得.
2.A 解析：∵ 反比例函数的图象位于第二、四象限，∴ k-1＜0, ∴ k＜1.只有A项符合题意.
3.C 解析： ∵ 点A、B都在反比例函数的图象上，∴ A（－1，6），B（－3，2）.设直线AB的解析式为，则解得
∴ 直线AB的解析式为，∴ C（－4，0）.在△中，OC＝4，OC边上的高（即点A到x轴的距离）为6，∴ △的面积在平面直角坐标系中求三角形的面积时，一般要将落在坐标轴上的一边作为底．
4.C 解析：抛物线y=向右平移1个单位长度后，所得函数的表达式为，抛物线向上平移2个单位长度后，所得函数的表达式为.
5.B 解析：把点（1,1）代入,得
6. D 解析：因为反比例函数的图象位于第一、三象限，且在每个象限内y随x的增大而减小，所以y1 >y2.又因为当x<0时，y<0，当x>0时，y>0，所以y3>0，y2 7. D 解析：由题意可知所以所以当
8. B 解析：因为当x取任意实数时，都有，又二次函数的图象开口向上，所以图象与x轴没有交点，所以
9.C 解析：分三段考虑：①开始录入时 ( http: / / www.21cnjy.com )，y随x的增大而缓慢增大；②因事暂停时，y随x的增大，不变；③最后录入时，y随x的增大而快速增大．
10. D 解析：∵ 抛物线与轴有两个交点，∴ 方程有两个不相等的实数根，∴ ，①正确.∵ 抛物线的开口向下，∴ .又∵ 抛物线的对称轴是直线，，∴ .∵ 抛物线与轴交于正半轴，∴ ，∴，②正确.方程的根是抛物线与直线交点的横坐标，当时，抛物线与直线没有交点，此时方程没有实数根，③正确，∴ 正确的结论有3个.
11. -1 解析：若两个变量x和y间的关系式可以表示成y=kx+b（k，b为常数，k≠0）的形式，则称y是x的一次函数（x为自变量，y为x的函数）.因而有=1，解得m=±1.又m-1≠0，∴ m=-1.
12. 解析：观察图象知：y随x的增大而减小，且x=2时y=3,故y<3时x>2.
13.k＞0 解析：本 ( http: / / www.21cnjy.com )题考查了一次函数的图象与性质.因为直线与y轴交于正半轴，且过第一、二、三象限，所以y随x的增大而增大，所以k＞0.
14. 0 解析：根据二次函数的定义，得，解得.
又∵ ，∴ .∴ 当时，这个函数是二次函数.
15. 解析：
16. 解析：根据题意，有t = ，∴ k = .因此，B，C两个城市间每天的电话通话次数为TBC=k×错误！未指定书签。.
17. k<- 解析：若一次函数y=kx+1的图象与反比例函数y=的图象没有公共点，则方程kx+1=没有实数根，将方程整理得，解得k<-.
18. 解析：把（-1，0）和（0，-1）两点的坐标分别代入中，得
，∴ .
由图象可知，抛物线的对称轴为直线，且，
∴∴.
∴
=，故填.
19.（1）证法一：因为（–2m）2–4（m2+3）= –12＜0，
所以方程x2–2mx+m2+3=0没有实数根，
所以不论为何值，函数的图象与x轴没有公共点.
证法二：因为，所以该函数的图象开口向上.
又因为，
所以该函数的图象在轴的上方.
所以不论为何值，该函数的图象与轴没有公共点.
（2）解：，
把函数的图象沿y轴向下平移3个单位长度后，得到函数的图象，它的顶点坐标是（m，0），
因此，这个函数的图象与轴只有一个公共点.
所以把函数的图象沿轴向下平移3个单位长度后，得到的函数的图象与轴只有一个公共点．
20.解：(1)由图中条件可知，反比例函数的图象经过点A(2，1)，
∴ 1＝，∴ m＝2，∴ 反比例函数的解析式为y＝.
又点B也在反比例函数的图象上，∴ n＝＝-2，
∴ 点B的坐标为(-1，-2).
∵ 直线y＝kx+b经过点A，B，
∴ 解得 ∴ 一次函数的解析式为y＝x-1.
(2)根据图象可知，一次函数的图象在反比例函数的图象的上方时，一次函数的值大于反比例函数的值，即x＞2或-1＜x＜0.
21.解：能.∵ ，∴ 顶点的坐标为(4，3).
设抛物线的解析式为 +3，
把点的坐标代入上式，得 ，∴，
∴ 即.
令，得∴(舍去)，
故该运动员的成绩为.
22.分析：（1）等量关系：2个A品牌 ( http: / / www.21cnjy.com )计算器的费用+3个B品牌计算器的费用=156元，3个A品牌计算器的费用+1个B品牌计算器的费用=122元；（2）根据“y1=0.8×A品牌计算器的单价×A品牌计算器的数量”写出y1关于x 的函数解析式，而写y2关于x 的函数解析式时，要分“0≤x≤5”和“x>5”两种情况讨论；（3）由y1>y2，y1= y2，y1解：（1）设A品牌计算器的单价为x元，B品牌计算器的单价为y元.
根据题意，得解得
即A，B两种品牌计算器的单价分别为30元和32元.
（2）根据题意，得y1=0.8×30x，即y1=24x.
当0≤x≤5时，y2=32x;
当x>5时，y2＝32×5+32×0.7（x-5），
即y2=22.4x+48.
（3）当购买数量超过5个时，y2=22.4x+48.
①当y1故当购买数量超过5个而不足30个时，购买A品牌的计算器更合算.
②当y1＝y2时，24x＝22.4x+48，∴ x＝30.
故当购买数量为30个时，购买A品牌与B品牌的计算器花费相同.
③当y1>y2时， 24x>22.4x+48，∴ x>30.
故当购买数量超过30个时，购买B品牌的计算器更合算.
点拨：选择优惠方法时，要通过比较函数值的大小来确定选择哪种方法，本题体现了分类讨论的数学思想.
23.解：（1）∵ 抛物线与轴有两个不同的交点，
∴ ＞0，即解得c＜.
(2)设抛物线与轴的两交点的横坐标分别为，
∵ 两交点间的距离为2，∴ .
由题意，得，解得，
∴ ，.
24.分析：（1）把q=35分别代入q=30+ x 和q=20+ 中求出x；
（2）根据“第x天获得的利润=第x天每件商品的利润×第x天的销售量p”写出y与x之间的函数解析式；
（3）分两种情况求出最大利润后进行比较，从中选取利润最大的作为最后的结果.
解：（1）当1≤x≤20时，令30+x=35，得x=10.
当21≤x≤40时，令20+=35，得x=35.
即第10天或第35天该商品的销售单价为35元/件.
（2）当1≤x≤20时，y=（30+x-20）（50-x）= - x2+15x+500;
当21≤x≤40时，y=（20+-20）（50-x）=-525.
∴
（3）当1≤x≤20时，y= -x2+15x+500= -（x-15）2+612.5.
∵ -<0，∴ 当x=15时，y有最大值y1，且y1=612.5.
当21≤x≤40时，∵ 26 250>0，∴ 随着x的增大而减小，
∴ 当x=21时，最大.
于是，当x=21时，y = -525有最大值y2，且y2= -525=725.
∵ y1点拨：本题为分段函数问题，因此应先根据自变量的不同取值范围确定不同的函数解析式，再根据不同函数的性质确定最大（小）值.
第3题图
第10题图
第12题图
第18题图
第19题答图