青岛版九年级数学下册6.6 简单的概率计算(第1课时)
文档属性
| 名称 | 青岛版九年级数学下册6.6 简单的概率计算(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 950.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览






文档简介
课件16张PPT。 6.6简单的概率计算
第1课时1.在具体情景中进一步了解概率的意义,体会概率是描述不确定现象的数学模型;
2.了解一类事件发生概率的计算方法,并能进行简单计算. 在同样条件下,某一随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢? 能否用数值进行刻画呢?这是我们下面要讨论的问题.实验1
从分别标有1、2、3、4、5号的5根纸签中随机地抽取一根, 抽出的签上的号码有几种可能?每个号被抽到的可能性大小相同吗? 每个号被抽到的可能性大小相同,都是全部可能结果
总数的 . 抽出的签上的号码有5种可能,即
1、2、3、4、5.实验2 掷一枚骰子,向上一面的点数有几种可能?每种
可能性出现的大小相同吗?向上一面的点数有6种可能,即
1、2、3、4、5、6.每个点数向上的可能性大小相同,都是全部可能结
果总数的 . 一般地,如果一次试验中,有n种可能的结果,并且它们发
生的可能性都相等.事件A包含其中的m种结果.那么事件发生
的概率P(A)= .可以发现以上试验有两个共同点:
1.每一次试验中,可能出现的结果是有限个;
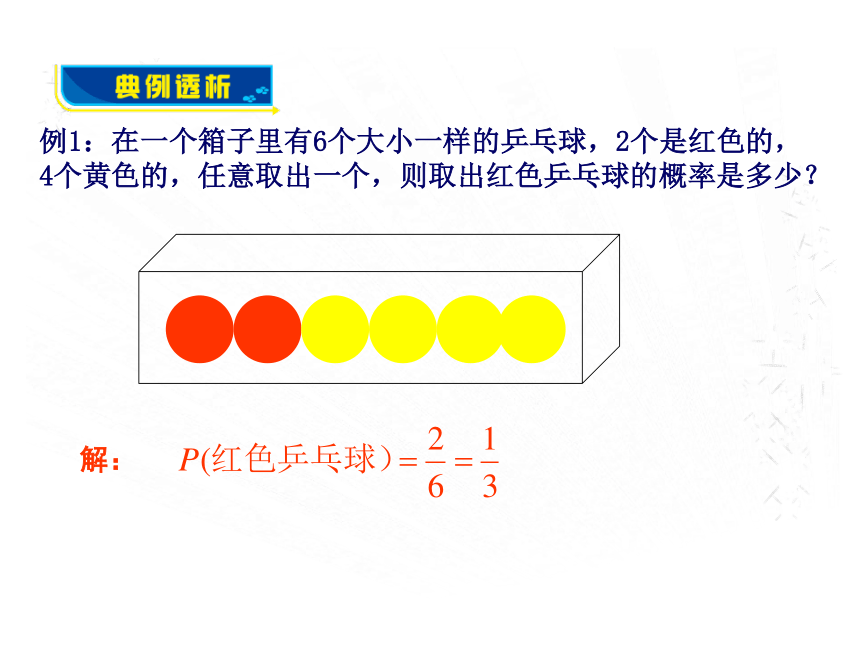
2.每一次试验中,出现的结果可能性相等.例1:在一个箱子里有6个大小一样的乒乓球,2个是红色的,
4个黄色的,任意取出一个,则取出红色乒乓球的概率是多少?解:例2:掷一枚骰子,
上面的点数分别为1,2,3,4,5,6,落点后,
(1)骰子朝上一面的“点数不大于6”是什么事件?它的概率是多少?
(2)骰子朝上一面的“点数是质数”是什么事件?它的概率是多少?
(3)骰子朝上一面的“两次点数之和是13”是什么事件?它的概率是多少?
(1)点数不大于6是必然事件(2 )点数是质数随机事件解:(3)两次点数之和是13”是不可能事件 事件发生的概率越大,它的概率越接近于1,反之,事件发生的概率越小,它的概率越接近于0.因此:0≤P(A)≤1 必然事件的概率和不可能事件的概率分别是多少呢?当为必然事件时P(A) =1,
当为不可能事件时,P(A) =0. 1.明天下雨的概率为95%,那么下列说法错误的是( )(A)明天下雨的可能性较大(B)明天不下雨的可能性较小(C)明天有可能是晴天(D)明天不可能是晴天D(1)P(掷出的点数小于4)= 2.任意掷一枚均匀的骰子, (3)P(掷出的点数是7)=(4)P(掷出的点数小于7)=013.文具盒中有4支铅笔,3支圆珠笔,1支钢笔,下列说法
表述正确的是( )
A.P(取到铅笔)=
B.P(取到圆珠笔)=
C.P(取到圆珠笔)=
D.P(取到钢笔)=1C4.小明和小颖做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(不放回),谁摸到的牌面大,谁就获胜。现小明已经摸到的牌面为4,然后小颖摸牌,P(小明获胜)= .事件发生的概率越大,它的概率越接近于1,反之,事件发生
的概率越小,它的概率越接近于0. 0≤P(A)≤1.
当为必然事件时P(A) =1,当为不可能事件时,P(A) =0.再见
第1课时1.在具体情景中进一步了解概率的意义,体会概率是描述不确定现象的数学模型;
2.了解一类事件发生概率的计算方法,并能进行简单计算. 在同样条件下,某一随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢? 能否用数值进行刻画呢?这是我们下面要讨论的问题.实验1
从分别标有1、2、3、4、5号的5根纸签中随机地抽取一根, 抽出的签上的号码有几种可能?每个号被抽到的可能性大小相同吗? 每个号被抽到的可能性大小相同,都是全部可能结果
总数的 . 抽出的签上的号码有5种可能,即
1、2、3、4、5.实验2 掷一枚骰子,向上一面的点数有几种可能?每种
可能性出现的大小相同吗?向上一面的点数有6种可能,即
1、2、3、4、5、6.每个点数向上的可能性大小相同,都是全部可能结
果总数的 . 一般地,如果一次试验中,有n种可能的结果,并且它们发
生的可能性都相等.事件A包含其中的m种结果.那么事件发生
的概率P(A)= .可以发现以上试验有两个共同点:
1.每一次试验中,可能出现的结果是有限个;
2.每一次试验中,出现的结果可能性相等.例1:在一个箱子里有6个大小一样的乒乓球,2个是红色的,
4个黄色的,任意取出一个,则取出红色乒乓球的概率是多少?解:例2:掷一枚骰子,
上面的点数分别为1,2,3,4,5,6,落点后,
(1)骰子朝上一面的“点数不大于6”是什么事件?它的概率是多少?
(2)骰子朝上一面的“点数是质数”是什么事件?它的概率是多少?
(3)骰子朝上一面的“两次点数之和是13”是什么事件?它的概率是多少?
(1)点数不大于6是必然事件(2 )点数是质数随机事件解:(3)两次点数之和是13”是不可能事件 事件发生的概率越大,它的概率越接近于1,反之,事件发生的概率越小,它的概率越接近于0.因此:0≤P(A)≤1 必然事件的概率和不可能事件的概率分别是多少呢?当为必然事件时P(A) =1,
当为不可能事件时,P(A) =0. 1.明天下雨的概率为95%,那么下列说法错误的是( )(A)明天下雨的可能性较大(B)明天不下雨的可能性较小(C)明天有可能是晴天(D)明天不可能是晴天D(1)P(掷出的点数小于4)= 2.任意掷一枚均匀的骰子, (3)P(掷出的点数是7)=(4)P(掷出的点数小于7)=013.文具盒中有4支铅笔,3支圆珠笔,1支钢笔,下列说法
表述正确的是( )
A.P(取到铅笔)=
B.P(取到圆珠笔)=
C.P(取到圆珠笔)=
D.P(取到钢笔)=1C4.小明和小颖做摸牌游戏,他们先后从这副去掉大、小王的扑克牌中任意抽取一张牌(不放回),谁摸到的牌面大,谁就获胜。现小明已经摸到的牌面为4,然后小颖摸牌,P(小明获胜)= .事件发生的概率越大,它的概率越接近于1,反之,事件发生
的概率越小,它的概率越接近于0. 0≤P(A)≤1.
当为必然事件时P(A) =1,当为不可能事件时,P(A) =0.再见
