青岛版九年级数学下册5.7 二次函数的应用(第2课时)
文档属性
| 名称 | 青岛版九年级数学下册5.7 二次函数的应用(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览





文档简介
课件25张PPT。5.7 二次函数的应用
第2课时1.会建立直角坐标系解决实际问题;
2.会应用二次函数的性质解决实际问题.
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为一个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
(3)如果各磁道的存储单元数目与最内
磁道相同,最内磁道的半径r是多少时,
磁盘的存储量最大?计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,现有一张半径为45mm的磁盘,你能说出r为多少时y最大吗?分析(1)最内磁道的周长为2πr ㎜,它上面的存储单元的个数不超过 (2)由于磁盘上磁道之间的宽度必须不小于0.3㎜,磁盘的外圆周不是磁道,各磁道分布在磁盘上内径为r mm外径为 45 mm的圆环区域,所以这张磁盘最多有 条磁道.
(3)当各磁道的存储单元数目与最内磁道相同时,磁盘每面存储量=每条磁道的存储单元数x磁道数.
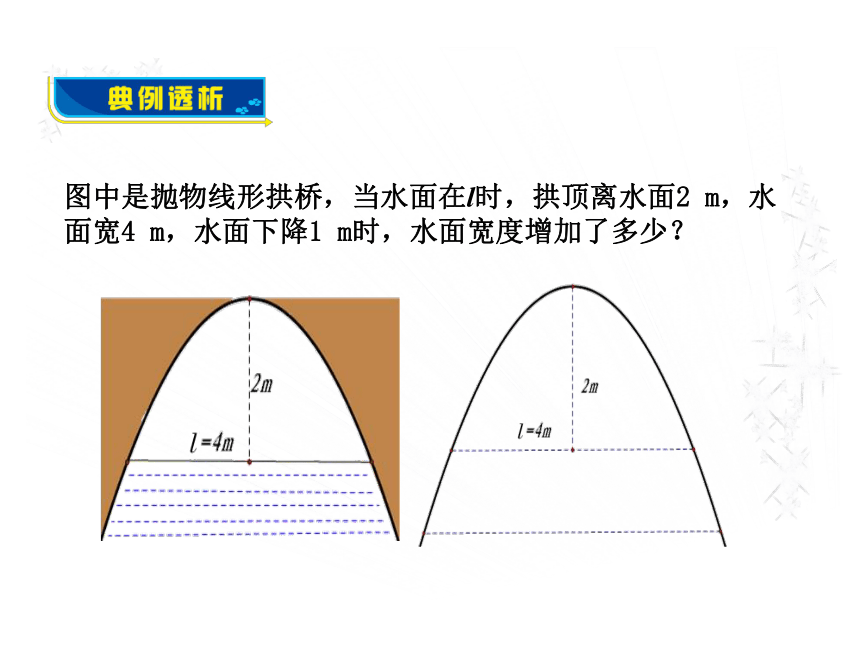
设磁盘每面存储量为y,则(0二次函数的解析式为:此时,抛物线的顶点为(0,2)当拱桥离水面2 m时,水面宽4 m即:抛物线过点(2,0)∴这条抛物线所表示的二次函数为:当水面下降1 m时,水面的纵坐标为y=-1,这时有:∴当水面下降1 m时,水面宽度增加了解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.∴可设这条抛物线所表示的二次函数的解析式为:∵抛物线过点(0,0)∴这条抛物线所表示的二次函数为:此时,抛物线的顶点为(2,2)当水面下降1 m时,水面的纵坐标为y=-1,这时有:∴当水面下降1 m时,水面宽度增加了∴这时水面的宽度为:1.理解问题;回顾解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.2.分析问题中的变量和常量,以及它们之间的关系3.用数学的方式表示出它们之间的关系;4.求解;5.检验结果的合理性“二次函数应用”的思路 1.如图,等腰Rt△ABC(∠ACB=90o)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )A2.如图所示,阳光中学教学楼前喷水池
喷出的抛物线形水柱,其解析式
为 ,则水柱的最大高度
是( )
A.2 B.4 C.6 D.2+
3.已知二次函数 的
图象如图所示,有下列5个结论:①
abc>0; ②b0;④2c<3b;
⑤ a+b>m(am+b)(m为不等于1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个CB4.某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4 m,顶部C离地面的高度为4.4 m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7 m,装货宽度为2.4 m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.解析:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.∵AB=4∴A(-2,0) B(2,0)∵OC=4.4∴C(0,4.4)设抛物线所表示的二次函数为∵抛物线过A(-2,0)∴抛物线所表示的二次函数为∴汽车能顺利经过大门.7.2816.24.42.11.1y2.1x2>=+′-==时,当5.某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数图象如图:
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,
为了获得最大利润,工厂每天应
安排使用多少度电?工厂每天
消耗电产生利润最大是多少元?【解析】(1)工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b.该函数图象过点(0,300),(500,200)
∴ 500k+b=200 解得 k=-
b=300 b= 300
∴y=- x+300(x≥0)
当电价x=600元/千度时,该工厂消耗每千度电产生利润y= 600+300=180(元/千度)
(2)设工厂每天消耗电产生利润为w元,由题意得:
W=my=m(- x+300)=m [- (10m+500)+300]
化简配方,得:w=-2(m-50)2+5000
由题意,m≤60, ∴当m=50时,w最大=5000
即当工厂每天消耗50千度电时,工厂每天消耗电产生利润最大为5000元.抽象转化数学问题运用数学知识解决问题解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.实际问题再见
第2课时1.会建立直角坐标系解决实际问题;
2.会应用二次函数的性质解决实际问题.
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为一个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
(3)如果各磁道的存储单元数目与最内
磁道相同,最内磁道的半径r是多少时,
磁盘的存储量最大?计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,现有一张半径为45mm的磁盘,你能说出r为多少时y最大吗?分析(1)最内磁道的周长为2πr ㎜,它上面的存储单元的个数不超过 (2)由于磁盘上磁道之间的宽度必须不小于0.3㎜,磁盘的外圆周不是磁道,各磁道分布在磁盘上内径为r mm外径为 45 mm的圆环区域,所以这张磁盘最多有 条磁道.
(3)当各磁道的存储单元数目与最内磁道相同时,磁盘每面存储量=每条磁道的存储单元数x磁道数.
设磁盘每面存储量为y,则(0
喷出的抛物线形水柱,其解析式
为 ,则水柱的最大高度
是( )
A.2 B.4 C.6 D.2+
3.已知二次函数 的
图象如图所示,有下列5个结论:①
abc>0; ②b
⑤ a+b>m(am+b)(m为不等于1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个CB4.某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4 m,顶部C离地面的高度为4.4 m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7 m,装货宽度为2.4 m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.解析:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.∵AB=4∴A(-2,0) B(2,0)∵OC=4.4∴C(0,4.4)设抛物线所表示的二次函数为∵抛物线过A(-2,0)∴抛物线所表示的二次函数为∴汽车能顺利经过大门.7.2816.24.42.11.1y2.1x2>=+′-==时,当5.某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数图象如图:
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,
为了获得最大利润,工厂每天应
安排使用多少度电?工厂每天
消耗电产生利润最大是多少元?【解析】(1)工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b.该函数图象过点(0,300),(500,200)
∴ 500k+b=200 解得 k=-
b=300 b= 300
∴y=- x+300(x≥0)
当电价x=600元/千度时,该工厂消耗每千度电产生利润y= 600+300=180(元/千度)
(2)设工厂每天消耗电产生利润为w元,由题意得:
W=my=m(- x+300)=m [- (10m+500)+300]
化简配方,得:w=-2(m-50)2+5000
由题意,m≤60, ∴当m=50时,w最大=5000
即当工厂每天消耗50千度电时,工厂每天消耗电产生利润最大为5000元.抽象转化数学问题运用数学知识解决问题解题步骤:
1.分析题意,把实际问题转化为数学问题,画出图形.
2.根据已知条件建立适当的平面直角坐标系.
3.选用适当的解析式求解.
4.根据二次函数的解析式解决具体的实际问题.实际问题再见
