5.4二次函数的图像与性质(第2课时)课件
文档属性
| 名称 | 5.4二次函数的图像与性质(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 951.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-25 00:00:00 | ||
图片预览




文档简介
课件16张PPT。5.4 二次函数的图象和性质
第2课时1.会画二次函数 与 的图象;
2.知道二次函数 及 与 的联系;
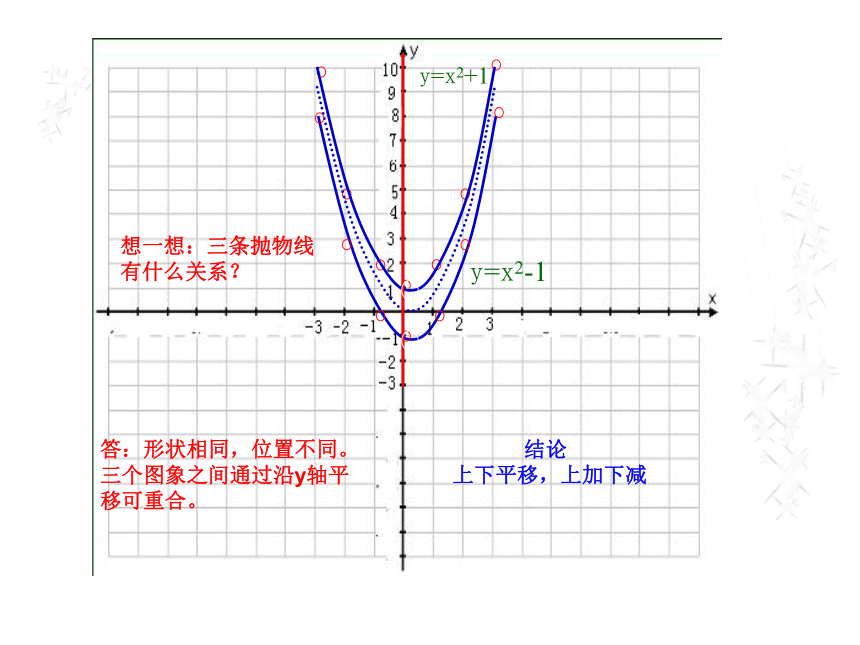
3.掌握二次函数 及 的性质,并会应用. 用描点法画出y=-2x2的图象,并指出它的开口方向、对称轴以及顶点坐标.参照下表画出函数y=x2+1与y=x2-1的图象.y=x2-1y=x2+1 结论
上下平移,上加下减想一想:三条抛物线
有什么关系?答:形状相同,位置不同。
三个图象之间通过沿y轴平
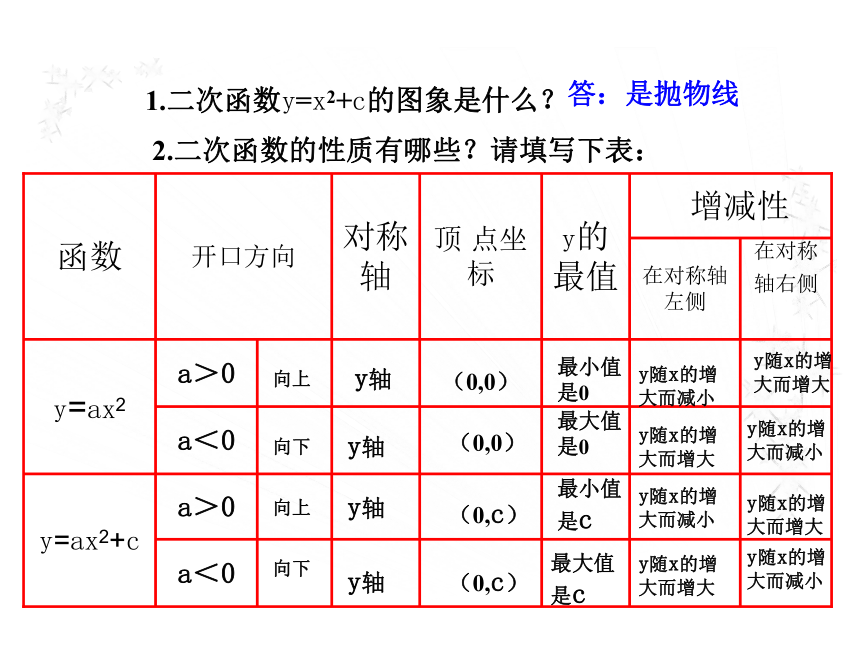
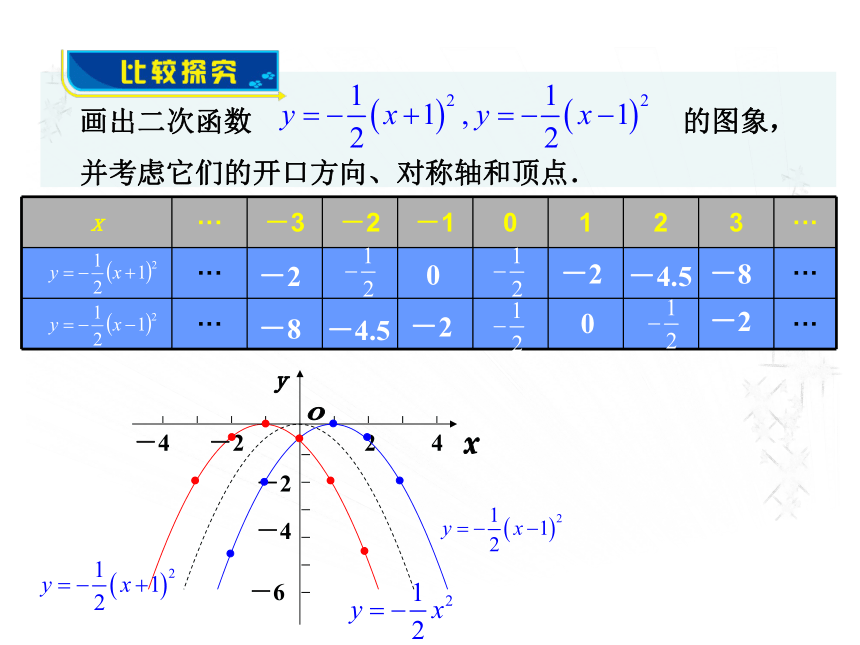
移可重合。1.二次函数y=x2+c的图象是什么?答:是抛物线2.二次函数的性质有哪些?请填写下表:画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.-2-8-4.5-200-2-8-4.5-2 可以看出,抛物线 的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线 的开口向_________,对称轴是________________,顶点是_________________.下x = 1( 1 , 0 )抛物线 与抛物线 有什么关系?可以发现,把抛物线 向左平移1个单位,就得到抛物线 ;把抛物线 向右平移1个单位,就得到抛物线 .a>0时,开口_____, 最 ____ 点是顶点;
a<0时,开口_____, 最 ____ 点是顶点;
对称轴是 , 顶点坐标是
在对称轴左侧(x<-h)y随x的增大而…..y=ax2y=a(x+h)2的图象y=a(x-h)2当向左平移h时向下向上高直线x=-h(-h,0)低y=a(x+h)2当向右平移h时a>0时,开口_____, 最 ____ 点是顶点;
a<0时,开口_____, 最 ____ 点是顶点;
对称轴是 , 顶点坐标是 。在对称轴左侧(x1.抛物线y=0.5(x+2)2可以由抛物线 先向 移2个单位得到.
2.已知s= –(x+1)2,当x为 时,s取最 值 为 .
3.顶点坐标为(1,0),且经过(0,-1)的抛物线的函数解析式是( ).
y=(x+1)2 B. y= –(x+1)2
C.y=(x–1)2 D. y= –(x–1)2y=0.5x2左 –1 大0 D上y轴(0,0)抛物0小增大0减小5.函数y=-2x2+4的图象开口向____,对称轴是_____,顶点坐标是_______,当x=____时,函数有最____值为____;当x<0时,y随x的增大而_______,当x>0时, y随x的增大_______。下y轴(0,4)减小增大04大6.函数y =-2(x+1)2的图象开口向____,对称轴是________,
顶点坐标是_______,当x=____时,函数有最____值为____;
当x_____时,y随x的增大而增大,当x_____时, y随x的增大
而减小.下直线x=-1(-1,0)-1大0< -1> -17.抛物线y=3x2-4,y=3(x-1)2与抛物线y=3x2的_______相同,_______不同。抛物线y=3x2-4是由抛物线y=3x2向____平移____单位而得到;抛物线y=3(x-1)2是由抛物线y=3x2向____平移____单位而得到.形状位置下4右1向上向上向下向下y 轴y 轴y 轴y 轴(0,0)(0,k)(0,0)(0,k) 向上 向上向下向下y轴x = -hy轴y = h(0,0)(h,0)(0,0)(-h,0)y = ax2y = ax2 + k y = a(x – h )2上下平移左右平移上下平移,上加下减 左右平移,左加右减 再见
第2课时1.会画二次函数 与 的图象;
2.知道二次函数 及 与 的联系;
3.掌握二次函数 及 的性质,并会应用. 用描点法画出y=-2x2的图象,并指出它的开口方向、对称轴以及顶点坐标.参照下表画出函数y=x2+1与y=x2-1的图象.y=x2-1y=x2+1 结论
上下平移,上加下减想一想:三条抛物线
有什么关系?答:形状相同,位置不同。
三个图象之间通过沿y轴平
移可重合。1.二次函数y=x2+c的图象是什么?答:是抛物线2.二次函数的性质有哪些?请填写下表:画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.-2-8-4.5-200-2-8-4.5-2 可以看出,抛物线 的开口向下,对称轴是经过点(-1,0)且与x轴垂直的直线,我们把它记作x=-1,顶点是(-1,0);抛物线 的开口向_________,对称轴是________________,顶点是_________________.下x = 1( 1 , 0 )抛物线 与抛物线 有什么关系?可以发现,把抛物线 向左平移1个单位,就得到抛物线 ;把抛物线 向右平移1个单位,就得到抛物线 .a>0时,开口_____, 最 ____ 点是顶点;
a<0时,开口_____, 最 ____ 点是顶点;
对称轴是 , 顶点坐标是
在对称轴左侧(x<-h)y随x的增大而…..y=ax2y=a(x+h)2的图象y=a(x-h)2当向左平移h时向下向上高直线x=-h(-h,0)低y=a(x+h)2当向右平移h时a>0时,开口_____, 最 ____ 点是顶点;
a<0时,开口_____, 最 ____ 点是顶点;
对称轴是 , 顶点坐标是 。在对称轴左侧(x
2.已知s= –(x+1)2,当x为 时,s取最 值 为 .
3.顶点坐标为(1,0),且经过(0,-1)的抛物线的函数解析式是( ).
y=(x+1)2 B. y= –(x+1)2
C.y=(x–1)2 D. y= –(x–1)2y=0.5x2左 –1 大0 D上y轴(0,0)抛物0小增大0减小5.函数y=-2x2+4的图象开口向____,对称轴是_____,顶点坐标是_______,当x=____时,函数有最____值为____;当x<0时,y随x的增大而_______,当x>0时, y随x的增大_______。下y轴(0,4)减小增大04大6.函数y =-2(x+1)2的图象开口向____,对称轴是________,
顶点坐标是_______,当x=____时,函数有最____值为____;
当x_____时,y随x的增大而增大,当x_____时, y随x的增大
而减小.下直线x=-1(-1,0)-1大0< -1> -17.抛物线y=3x2-4,y=3(x-1)2与抛物线y=3x2的_______相同,_______不同。抛物线y=3x2-4是由抛物线y=3x2向____平移____单位而得到;抛物线y=3(x-1)2是由抛物线y=3x2向____平移____单位而得到.形状位置下4右1向上向上向下向下y 轴y 轴y 轴y 轴(0,0)(0,k)(0,0)(0,k) 向上 向上向下向下y轴x = -hy轴y = h(0,0)(h,0)(0,0)(-h,0)y = ax2y = ax2 + k y = a(x – h )2上下平移左右平移上下平移,上加下减 左右平移,左加右减 再见
